人教A版(2019)高中数学选择性必修第二册 【整合课件】5.3.1函数的单调性 课件(共32张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 【整合课件】5.3.1函数的单调性 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 14:06:06 | ||
图片预览










文档简介
(共32张PPT)
§5.3 导数在研究函数中的应用
5.3.1 函数的单调性与导数(一)
学习目标
1.理解导数与函数的单调性的关系.
2.掌握利用导数判断函数单调性的方法.
3.能利用导数求不超过三次多项式函数的单调区间.
问题导学
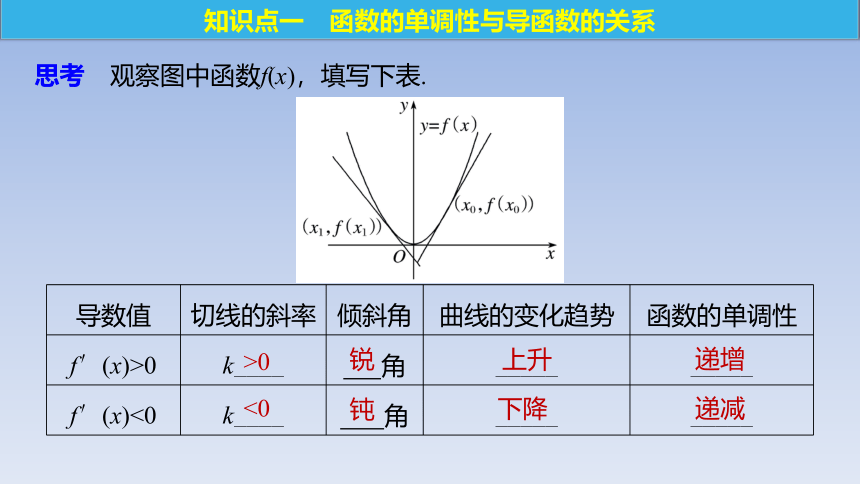
导数值 切线的斜率 倾斜角 曲线的变化趋势 函数的单调性
f′(x)>0 k____ 角 _____ _____
f′(x)<0 k____ 角 _____ _____
知识点一 函数的单调性与导函数的关系
思考 观察图中函数f(x),填写下表.
>0
<0
锐
钝
上升
下降
递增
递减
梳理 一般地,设函数y=f(x)在区间(a,b)内可导,则在区间(a,b)内,
(1)如果f′(x)>0,则f(x)在这个区间内 ;
(2)如果f′(x)<0,则f(x)在这个区间内 .
单调递增
单调递减
(1)确定函数y=f(x)的定义域;
(2)求导数y′=f′(x);
(3)解不等式 ,解集在定义域内的部分为增区间;
(4)解不等式 ,解集在定义域内的部分为减区间.
知识点二 利用导数判断函数的单调性的一般步骤
f′(x)>0
f′(x)<0
1.函数f(x)在定义域上都有f′(x)<0,则函数f(x)在定义域上单调递减.
( )
2.函数f(x)在某区间内单调递增,则一定有f′(x)>0.( )
[思考辨析 判断正误]
×
×
题型探究
类型一 函数图象与导数图象的应用
例1 已知函数y=f(x)的定义域为[-1,5],部分对应值如下表.f(x)的导函数y=f′(x)的图象如图所示.
x -1 0 4 5
f(x) 1 2 2 1
给出下列关于函数f(x)的说法:
①函数y=f(x)是周期函数; ②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1其中正确说法的个数是
A.4 B.3 C.2 D.1
√
解析 依题意得,函数f(x)不可能是周期函数,因此①不正确;
当x∈(0,2)时,f′(x)<0,因此函数f(x)在[0,2]上是减函数,②正确;
当x∈[-1,t]时,若f(x)的最大值是2,则结合函数f(x)的可能图象分析可知,此时t的最大值是5,因此③不正确;
注意到f(2)的值不明确,结合函数f(x)的可能图象分析可知,将函数f(x)的图象向下平移a(1反思与感悟 (1)函数的单调性与其导函数的正负的关系:在某个区间(a,b)内,若f′(x)>0,则y=f(x)在(a,b)上单调递增;如果f′(x)<0,则y=f(x)在这个区间上单调递减;若恒有f′(x)=0,则y=f(x)是常数函数,不具有单调性.
(2)函数图象变化得越快,f′(x)的绝对值越大,不是f′(x)的值越大.
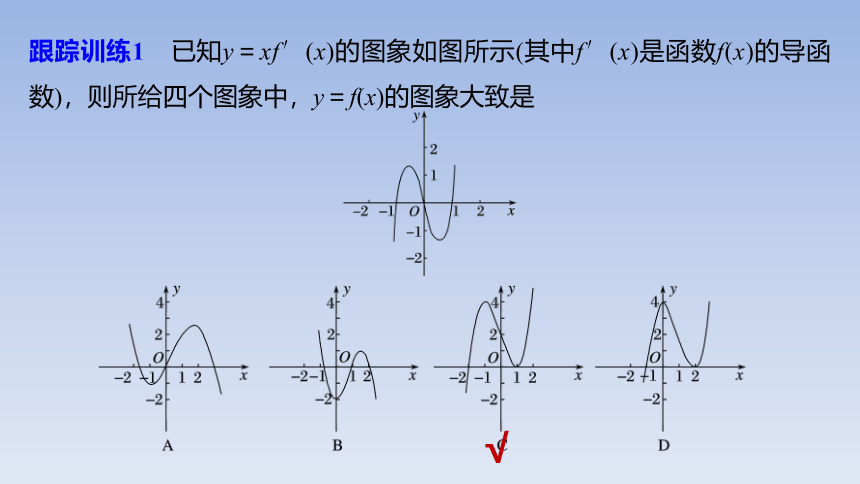
跟踪训练1 已知y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则所给四个图象中,y=f(x)的图象大致是
√
解析 当0∴f′(x)<0,故f(x)在(0,1)上为减函数;
当x>1时,xf′(x)>0,∴f′(x)>0,
故y=f(x)在(1,+∞)上为增函数.
故选C.
类型二 利用导数求函数的单调区间
命题角度1 不含参数的函数求单调区间
例2 求下列函数的单调区间.
解 函数f(x)的定义域为(-∞,0)∪(0,+∞),
反思与感悟 求函数y=f(x)的单调区间的步骤
(1)确定函数y=f(x)的定义域.
(2)求导数y′=f′(x).
(3)解不等式f′(x)>0,函数在解集所表示的定义域内为增函数.
(4)解不等式f′(x)<0,函数在解集所表示的定义域内为减函数.
跟踪训练2 函数f(x)=(x2+2x)ex(x∈R)的单调递减区间为____________________.
解析 由f′(x)=(x2+4x+2)ex<0,即x2+4x+2<0,
命题角度2 含参数的函数求单调区间
解 函数f(x)的定义域为(0,+∞),
由f′(x)>0,得x>1,由f′(x)<0,得0∴f(x)在(0,1)内为减函数,在(1,+∞)内为增函数.
由f′(x)>0,得x>1,由f′(x)<0,得0∴f(x)在(0,1)内为减函数,在(1,+∞)内为增函数.
综上所述,当a≥0时,f(x)在(0,1)内为减函数,在(1,+∞)内为增函数.
反思与感悟 (1)讨论参数要全面,做到不重不漏.
(2)解不等式时若涉及分式不等式要注意结合定义域化简,也可转化为二次不等式求解.
跟踪训练3 设函数f(x)=ex-ax-2,求f(x)的单调区间.
解 f(x)的定义域为(-∞,+∞),f′(x)=ex-a.
若a≤0,则f′(x)>0,
所以f(x)在(-∞,+∞)上单调递增.
若a>0,则当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
所以f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
综上所述,当a≤0时,函数f(x)在(-∞,+∞)上单调递增;
当a>0时,f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
达标检测
1.函数f(x)=x+ln x
A.在(0,6)上是增函数
B.在(0,6)上是减函数
1
2
3
4
5
√
1
2
3
4
5
2.若函数f(x)的图象如图所示,则导函数f′(x)的图象可能为
√
解析 由f(x)的图象可知,函数f(x)的单调递增区间为(1,4),单调递减区间为(-∞,1)和(4,+∞),因此,当x∈(1,4)时,f′(x)>0,当x∈(-∞,1)或x∈(4,+∞)时,f′(x)<0,结合选项知选C.
3.函数f(x)=3+x·ln x的单调递增区间是
√
解析 f′(x)=ln x+1,令f′(x)>0,
1
2
3
4
5
4.若函数f(x)=x3+bx2+cx+d的单调递减区间为[-1,2],则b=____,c=_____.
1
2
3
4
5
-6
解析 f′(x)=3x2+2bx+c,
由题意知,f′(x)=0即3x2+2bx+c=0的两根为-1和2.
1
2
3
4
5
解 函数f(x)=kx-ln x的定义域为(0,+∞),
当k≤0时,kx-1<0,∴f′(x)<0,
则f(x)在(0,+∞)上单调递减.
5.试求函数f(x)=kx-ln x的单调区间.
1
2
3
4
5
综上所述,当k≤0时,f(x)的单调递减区间为(0,+∞);
1.导数的符号反映了函数在某个区间上的单调性,导数绝对值的大小反映了函数在某个区间或某点附近变化的快慢程度.
2.利用导数求函数f(x)的单调区间的一般步骤:
(1)确定函数f(x)的定义域;
(2)求导数f′(x);
(3)在函数f(x)的定义域内解不等式f′(x)>0和f′(x)<0;
(4)根据(3)的结果确定函数f(x)的单调区间.
规律与方法
§5.3 导数在研究函数中的应用
5.3.1 函数的单调性与导数(一)
学习目标
1.理解导数与函数的单调性的关系.
2.掌握利用导数判断函数单调性的方法.
3.能利用导数求不超过三次多项式函数的单调区间.
问题导学
导数值 切线的斜率 倾斜角 曲线的变化趋势 函数的单调性
f′(x)>0 k____ 角 _____ _____
f′(x)<0 k____ 角 _____ _____
知识点一 函数的单调性与导函数的关系
思考 观察图中函数f(x),填写下表.
>0
<0
锐
钝
上升
下降
递增
递减
梳理 一般地,设函数y=f(x)在区间(a,b)内可导,则在区间(a,b)内,
(1)如果f′(x)>0,则f(x)在这个区间内 ;
(2)如果f′(x)<0,则f(x)在这个区间内 .
单调递增
单调递减
(1)确定函数y=f(x)的定义域;
(2)求导数y′=f′(x);
(3)解不等式 ,解集在定义域内的部分为增区间;
(4)解不等式 ,解集在定义域内的部分为减区间.
知识点二 利用导数判断函数的单调性的一般步骤
f′(x)>0
f′(x)<0
1.函数f(x)在定义域上都有f′(x)<0,则函数f(x)在定义域上单调递减.
( )
2.函数f(x)在某区间内单调递增,则一定有f′(x)>0.( )
[思考辨析 判断正误]
×
×
题型探究
类型一 函数图象与导数图象的应用
例1 已知函数y=f(x)的定义域为[-1,5],部分对应值如下表.f(x)的导函数y=f′(x)的图象如图所示.
x -1 0 4 5
f(x) 1 2 2 1
给出下列关于函数f(x)的说法:
①函数y=f(x)是周期函数; ②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1
A.4 B.3 C.2 D.1
√
解析 依题意得,函数f(x)不可能是周期函数,因此①不正确;
当x∈(0,2)时,f′(x)<0,因此函数f(x)在[0,2]上是减函数,②正确;
当x∈[-1,t]时,若f(x)的最大值是2,则结合函数f(x)的可能图象分析可知,此时t的最大值是5,因此③不正确;
注意到f(2)的值不明确,结合函数f(x)的可能图象分析可知,将函数f(x)的图象向下平移a(1
(2)函数图象变化得越快,f′(x)的绝对值越大,不是f′(x)的值越大.
跟踪训练1 已知y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则所给四个图象中,y=f(x)的图象大致是
√
解析 当0
当x>1时,xf′(x)>0,∴f′(x)>0,
故y=f(x)在(1,+∞)上为增函数.
故选C.
类型二 利用导数求函数的单调区间
命题角度1 不含参数的函数求单调区间
例2 求下列函数的单调区间.
解 函数f(x)的定义域为(-∞,0)∪(0,+∞),
反思与感悟 求函数y=f(x)的单调区间的步骤
(1)确定函数y=f(x)的定义域.
(2)求导数y′=f′(x).
(3)解不等式f′(x)>0,函数在解集所表示的定义域内为增函数.
(4)解不等式f′(x)<0,函数在解集所表示的定义域内为减函数.
跟踪训练2 函数f(x)=(x2+2x)ex(x∈R)的单调递减区间为____________________.
解析 由f′(x)=(x2+4x+2)ex<0,即x2+4x+2<0,
命题角度2 含参数的函数求单调区间
解 函数f(x)的定义域为(0,+∞),
由f′(x)>0,得x>1,由f′(x)<0,得0
由f′(x)>0,得x>1,由f′(x)<0,得0
综上所述,当a≥0时,f(x)在(0,1)内为减函数,在(1,+∞)内为增函数.
反思与感悟 (1)讨论参数要全面,做到不重不漏.
(2)解不等式时若涉及分式不等式要注意结合定义域化简,也可转化为二次不等式求解.
跟踪训练3 设函数f(x)=ex-ax-2,求f(x)的单调区间.
解 f(x)的定义域为(-∞,+∞),f′(x)=ex-a.
若a≤0,则f′(x)>0,
所以f(x)在(-∞,+∞)上单调递增.
若a>0,则当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
所以f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
综上所述,当a≤0时,函数f(x)在(-∞,+∞)上单调递增;
当a>0时,f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
达标检测
1.函数f(x)=x+ln x
A.在(0,6)上是增函数
B.在(0,6)上是减函数
1
2
3
4
5
√
1
2
3
4
5
2.若函数f(x)的图象如图所示,则导函数f′(x)的图象可能为
√
解析 由f(x)的图象可知,函数f(x)的单调递增区间为(1,4),单调递减区间为(-∞,1)和(4,+∞),因此,当x∈(1,4)时,f′(x)>0,当x∈(-∞,1)或x∈(4,+∞)时,f′(x)<0,结合选项知选C.
3.函数f(x)=3+x·ln x的单调递增区间是
√
解析 f′(x)=ln x+1,令f′(x)>0,
1
2
3
4
5
4.若函数f(x)=x3+bx2+cx+d的单调递减区间为[-1,2],则b=____,c=_____.
1
2
3
4
5
-6
解析 f′(x)=3x2+2bx+c,
由题意知,f′(x)=0即3x2+2bx+c=0的两根为-1和2.
1
2
3
4
5
解 函数f(x)=kx-ln x的定义域为(0,+∞),
当k≤0时,kx-1<0,∴f′(x)<0,
则f(x)在(0,+∞)上单调递减.
5.试求函数f(x)=kx-ln x的单调区间.
1
2
3
4
5
综上所述,当k≤0时,f(x)的单调递减区间为(0,+∞);
1.导数的符号反映了函数在某个区间上的单调性,导数绝对值的大小反映了函数在某个区间或某点附近变化的快慢程度.
2.利用导数求函数f(x)的单调区间的一般步骤:
(1)确定函数f(x)的定义域;
(2)求导数f′(x);
(3)在函数f(x)的定义域内解不等式f′(x)>0和f′(x)<0;
(4)根据(3)的结果确定函数f(x)的单调区间.
规律与方法
