人教A版(2019)高中数学选择性必修第二册 【整合课件】5.3.1函数的单调性 课件(共27张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 【整合课件】5.3.1函数的单调性 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 14:06:38 | ||
图片预览








文档简介
(共27张PPT)
5.3.1 函数的单调性与导数(二)
学习目标
1.会利用导数证明一些简单的不等式问题.
2.掌握利用导数研究含参数的单调性的基本方法.
问题导学
1.函数的单调性与其导数正负的关系
定义在区间(a,b)内的函数y=f(x):
f′(x)的正负 f(x)的单调性
f′(x)>0 单调递___
f′(x)<0 单调递___
增
减
特别提醒:①若在某区间上有有限个点使f′(x)=0,其余的点恒有f′(x)>0,则f(x)仍为增函数(减函数的情形完全类似).
②f(x)为增函数的充要条件是对任意的x∈(a,b)都有f′(x)≥0且在(a,b)内的任一非空子区间上f′(x)不恒为0.
导数的绝对值 函数值变化 函数的图象
越大 ____ 比较“ ”(向上或向下)
越小 ____ 比较“ ”(向上或向下)
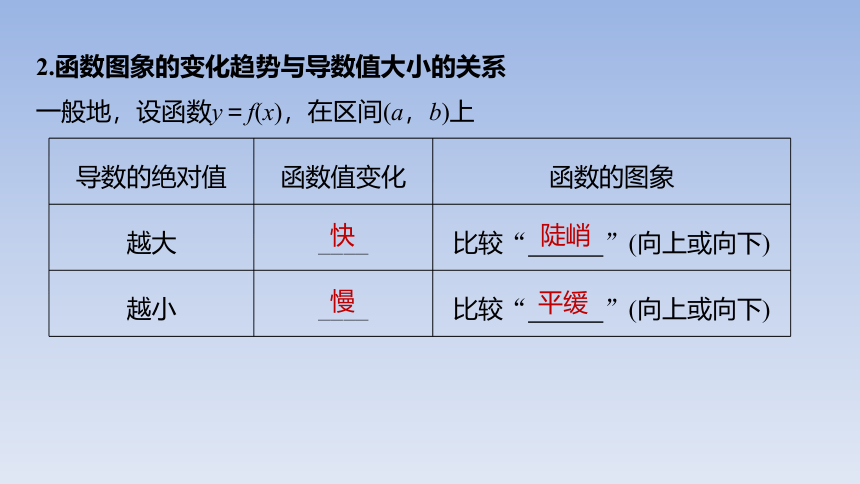
2.函数图象的变化趋势与导数值大小的关系
一般地,设函数y=f(x),在区间(a,b)上
快
慢
陡峭
平缓
3.利用导数解决单调性问题需要注意的问题
(1)定义域优先的原则:解决问题的过程只能在定义域内,通过讨论导数的符号来判断函数的单调区间.
(2)注意“临界点”和“间断点”:在对函数划分单调区间时,除了必须确定使导数等于零的点外,还要注意在定义域内的间断点.
(3)如果一个函数的单调区间不止一个,这些单调区间之间不能用“∪”连接,而只能用“逗号”或“和”字等隔开.
1.如果函数f(x)在某个区间内恒有f′(x)=0,则f(x)在此区间内没有单调性.
( )
2.函数在某区间上变化越快,函数在这个区间上的导数的绝对值越大.
( )
[思考辨析 判断正误]
√
√
题型探究
类型一 利用导数求参数的取值范围
例1 若函数f(x)=kx-ln x在区间(1,+∞)上单调递增,则k的取值范围是__________.
[1,+∞)
即k的取值范围为[1,+∞).
引申探究
1.若将本例中条件递增改为递减,求k的取值范围.
又f(x)在(1,+∞)上单调递减,
即k的取值范围为(-∞,0].
2.若将本例中条件递增改为不单调,求k的取值范围.
解 f(x)=kx-ln x的定义域为(0,+∞),
∴k的取值范围是(0,1).
当k≤0时,f′(x)<0.
∴f(x)在(0,+∞)上单调递减,故不合题意.
反思与感悟 (1)利用导数法解决取值范围问题的两个基本思路
①将问题转化为不等式在某区间上的恒成立问题,即f′(x)≥0(或f′(x)≤0)恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意;
②先令f′(x)>0(或f′(x)<0),求出参数的取值范围后,再验证参数取“=”时f(x)是否满足题意.
(2)恒成立问题的重要思路
①m≥f(x)恒成立 m≥f(x)max;
②m≤f(x)恒成立 m≤f(x)min.
解 方法一 (直接法)
f′(x)=x2-ax+a-1,
令f′(x)=0,得x=1或x=a-1.
当a-1≤1,即a≤2时,函数f(x)在(1,+∞)上单调递增,不合题意.
当a-1>1,即a>2时,函数f(x)在(-∞,1)和(a-1,+∞)上单调递增,在(1,a-1)上单调递减,
由题意知(1,4) (1,a-1)且(6,+∞) (a-1,+∞),
所以4≤a-1≤6,即5≤a≤7.
故实数a的取值范围为[5,7].
方法二 (数形结合法)
如图所示,
f′(x)=(x-1)[x-(a-1)].
因为在(1,4)内,f′(x)≤0,
在(6,+∞)内f′(x)≥0,
且f′(x)=0有一根为1,
所以另一根在[4,6]上.
故实数a的取值范围为[5,7].
方法三 (转化为不等式的恒成立问题)
f′(x)=x2-ax+a-1.
因为f(x)在(1,4)上单调递减,所以f′(x)≤0在(1,4)上恒成立.
即a(x-1)≥x2-1在(1,4)上恒成立,所以a≥x+1,
因为2又因为f(x)在(6,+∞)上单调递增,
所以f′(x)≥0在(6,+∞)上恒成立,所以a≤x+1,
因为x+1>7,所以当a≤7时,f′(x)≥0在(6,+∞)上恒成立.
综上知5≤a≤7.
故实数a的取值范围为[5,7].
例2 证明ex≥x+1≥sin x+1(x≥0).
证明 令f(x)=ex-x-1(x≥0),则f′(x)=ex-1≥0,
∴f(x)在[0,+∞)上单调递增,
∴对任意x∈[0,+∞),有f(x)≥f(0),而f(0)=0,
∴f(x)≥0,即ex≥x+1,
令g(x)=x-sin x(x≥0),g′(x)=1-cos x≥0,
∴g(x)≥g(0),即x-sin x≥0,
∴x+1≥sin x+1(x≥0),
综上,ex≥x+1≥sin x+1.
类型二 证明不等式
反思与感悟 用导数证明不等式f(x)>g(x)的一般步骤
(1)构造函数F(x)=f(x)-g(x),x∈[a,b].
(2)证明F′(x)=f′(x)-g′(x)≥0,且F(a)>0.
(3)依(2)知函数F(x)=f(x)-g(x)在[a,b]上是单调递增函数,故f(x)-g(x)>0,即f(x)>g(x).
这是因为F(x)为单调递增函数,
所以F(x)≥F(a)>0,
即f(x)-g(x)≥f(a)-g(a)>0.
当x>-1时,f′(x)>0,
则f(x)在(-1,+∞)内是增函数.
∴当x>0时,f(x)>f(0)=0.
达标检测
1.已知命题p:对任意x∈(a,b),有f′(x)>0,q:f(x)在(a,b)内是单调递增的,则p是q的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
1
2
3
4
5
√
1
2
3
4
5
2.已知对任意实数x,都有f(-x)=-f(x),g(-x)=g(x),且当x>0时,f′(x)>0,g′(x)>0,则当x<0时
A.f′(x)>0,g′(x)>0 B.f′(x)>0,g′(x)<0
C.f′(x)<0,g′(x)>0 D.f′(x)<0,g′(x)<0
√
解析 由题意知,f(x)是奇函数,g(x)是偶函数.
当x>0时,f(x),g(x)都单调递增,
则当x<0时,f(x)单调递增,g(x)单调递减,
即f′(x)>0,g′(x)<0.
3.已知函数f(x)=x3-12x,若f(x)在区间(2m,m+1)上单调递减,则实数m的取值范围是________.
解析 f′(x)≤0,即3x2-12≤0,得-2≤x≤2.
∴f(x)的减区间为[-2,2],
由题意得(2m,m+1) [-2,2],
[-1,1)
1
2
3
4
5
[2,+∞)
1
2
3
4
5
所以f(x)在(-∞,+∞)上为单调递增函数,其图象若穿越x轴,则只有一次穿越的机会,
显然x=0时,f(x)=0.
1
2
3
4
5
利用导数法解决取值范围问题的两个基本思路
(1)将问题转化为不等式在某区间上的恒成立问题,即f′(x)≥0(或f′(x)≤0)恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意;
(2)先令f′(x)>0(或f′(x)<0),求出参数的取值范围后,再验证参数取“=”时,f(x)是否满足题意.
规律与方法
5.3.1 函数的单调性与导数(二)
学习目标
1.会利用导数证明一些简单的不等式问题.
2.掌握利用导数研究含参数的单调性的基本方法.
问题导学
1.函数的单调性与其导数正负的关系
定义在区间(a,b)内的函数y=f(x):
f′(x)的正负 f(x)的单调性
f′(x)>0 单调递___
f′(x)<0 单调递___
增
减
特别提醒:①若在某区间上有有限个点使f′(x)=0,其余的点恒有f′(x)>0,则f(x)仍为增函数(减函数的情形完全类似).
②f(x)为增函数的充要条件是对任意的x∈(a,b)都有f′(x)≥0且在(a,b)内的任一非空子区间上f′(x)不恒为0.
导数的绝对值 函数值变化 函数的图象
越大 ____ 比较“ ”(向上或向下)
越小 ____ 比较“ ”(向上或向下)
2.函数图象的变化趋势与导数值大小的关系
一般地,设函数y=f(x),在区间(a,b)上
快
慢
陡峭
平缓
3.利用导数解决单调性问题需要注意的问题
(1)定义域优先的原则:解决问题的过程只能在定义域内,通过讨论导数的符号来判断函数的单调区间.
(2)注意“临界点”和“间断点”:在对函数划分单调区间时,除了必须确定使导数等于零的点外,还要注意在定义域内的间断点.
(3)如果一个函数的单调区间不止一个,这些单调区间之间不能用“∪”连接,而只能用“逗号”或“和”字等隔开.
1.如果函数f(x)在某个区间内恒有f′(x)=0,则f(x)在此区间内没有单调性.
( )
2.函数在某区间上变化越快,函数在这个区间上的导数的绝对值越大.
( )
[思考辨析 判断正误]
√
√
题型探究
类型一 利用导数求参数的取值范围
例1 若函数f(x)=kx-ln x在区间(1,+∞)上单调递增,则k的取值范围是__________.
[1,+∞)
即k的取值范围为[1,+∞).
引申探究
1.若将本例中条件递增改为递减,求k的取值范围.
又f(x)在(1,+∞)上单调递减,
即k的取值范围为(-∞,0].
2.若将本例中条件递增改为不单调,求k的取值范围.
解 f(x)=kx-ln x的定义域为(0,+∞),
∴k的取值范围是(0,1).
当k≤0时,f′(x)<0.
∴f(x)在(0,+∞)上单调递减,故不合题意.
反思与感悟 (1)利用导数法解决取值范围问题的两个基本思路
①将问题转化为不等式在某区间上的恒成立问题,即f′(x)≥0(或f′(x)≤0)恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意;
②先令f′(x)>0(或f′(x)<0),求出参数的取值范围后,再验证参数取“=”时f(x)是否满足题意.
(2)恒成立问题的重要思路
①m≥f(x)恒成立 m≥f(x)max;
②m≤f(x)恒成立 m≤f(x)min.
解 方法一 (直接法)
f′(x)=x2-ax+a-1,
令f′(x)=0,得x=1或x=a-1.
当a-1≤1,即a≤2时,函数f(x)在(1,+∞)上单调递增,不合题意.
当a-1>1,即a>2时,函数f(x)在(-∞,1)和(a-1,+∞)上单调递增,在(1,a-1)上单调递减,
由题意知(1,4) (1,a-1)且(6,+∞) (a-1,+∞),
所以4≤a-1≤6,即5≤a≤7.
故实数a的取值范围为[5,7].
方法二 (数形结合法)
如图所示,
f′(x)=(x-1)[x-(a-1)].
因为在(1,4)内,f′(x)≤0,
在(6,+∞)内f′(x)≥0,
且f′(x)=0有一根为1,
所以另一根在[4,6]上.
故实数a的取值范围为[5,7].
方法三 (转化为不等式的恒成立问题)
f′(x)=x2-ax+a-1.
因为f(x)在(1,4)上单调递减,所以f′(x)≤0在(1,4)上恒成立.
即a(x-1)≥x2-1在(1,4)上恒成立,所以a≥x+1,
因为2
所以f′(x)≥0在(6,+∞)上恒成立,所以a≤x+1,
因为x+1>7,所以当a≤7时,f′(x)≥0在(6,+∞)上恒成立.
综上知5≤a≤7.
故实数a的取值范围为[5,7].
例2 证明ex≥x+1≥sin x+1(x≥0).
证明 令f(x)=ex-x-1(x≥0),则f′(x)=ex-1≥0,
∴f(x)在[0,+∞)上单调递增,
∴对任意x∈[0,+∞),有f(x)≥f(0),而f(0)=0,
∴f(x)≥0,即ex≥x+1,
令g(x)=x-sin x(x≥0),g′(x)=1-cos x≥0,
∴g(x)≥g(0),即x-sin x≥0,
∴x+1≥sin x+1(x≥0),
综上,ex≥x+1≥sin x+1.
类型二 证明不等式
反思与感悟 用导数证明不等式f(x)>g(x)的一般步骤
(1)构造函数F(x)=f(x)-g(x),x∈[a,b].
(2)证明F′(x)=f′(x)-g′(x)≥0,且F(a)>0.
(3)依(2)知函数F(x)=f(x)-g(x)在[a,b]上是单调递增函数,故f(x)-g(x)>0,即f(x)>g(x).
这是因为F(x)为单调递增函数,
所以F(x)≥F(a)>0,
即f(x)-g(x)≥f(a)-g(a)>0.
当x>-1时,f′(x)>0,
则f(x)在(-1,+∞)内是增函数.
∴当x>0时,f(x)>f(0)=0.
达标检测
1.已知命题p:对任意x∈(a,b),有f′(x)>0,q:f(x)在(a,b)内是单调递增的,则p是q的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
1
2
3
4
5
√
1
2
3
4
5
2.已知对任意实数x,都有f(-x)=-f(x),g(-x)=g(x),且当x>0时,f′(x)>0,g′(x)>0,则当x<0时
A.f′(x)>0,g′(x)>0 B.f′(x)>0,g′(x)<0
C.f′(x)<0,g′(x)>0 D.f′(x)<0,g′(x)<0
√
解析 由题意知,f(x)是奇函数,g(x)是偶函数.
当x>0时,f(x),g(x)都单调递增,
则当x<0时,f(x)单调递增,g(x)单调递减,
即f′(x)>0,g′(x)<0.
3.已知函数f(x)=x3-12x,若f(x)在区间(2m,m+1)上单调递减,则实数m的取值范围是________.
解析 f′(x)≤0,即3x2-12≤0,得-2≤x≤2.
∴f(x)的减区间为[-2,2],
由题意得(2m,m+1) [-2,2],
[-1,1)
1
2
3
4
5
[2,+∞)
1
2
3
4
5
所以f(x)在(-∞,+∞)上为单调递增函数,其图象若穿越x轴,则只有一次穿越的机会,
显然x=0时,f(x)=0.
1
2
3
4
5
利用导数法解决取值范围问题的两个基本思路
(1)将问题转化为不等式在某区间上的恒成立问题,即f′(x)≥0(或f′(x)≤0)恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意;
(2)先令f′(x)>0(或f′(x)<0),求出参数的取值范围后,再验证参数取“=”时,f(x)是否满足题意.
规律与方法
