人教A版(2019)高中数学选择性必修第二册 【整合课件】5.3.2_函数的极值 课件(共38张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 【整合课件】5.3.2_函数的极值 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 14:07:49 | ||
图片预览











文档简介
(共38张PPT)
5.3.2 函数的极值与导数(一)
学习目标
1.了解函数极值的概念,会从几何方面直观理解函数的极值与导数的关系.
2.掌握函数极值的判定及求法.
3.掌握函数在某一点取得极值的条件.
问题导学
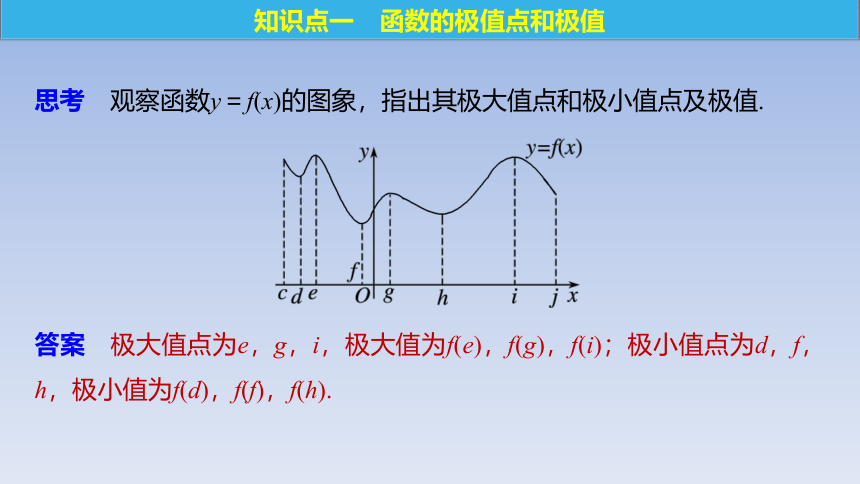
思考 观察函数y=f(x)的图象,指出其极大值点和极小值点及极值.
知识点一 函数的极值点和极值
答案 极大值点为e,g,i,极大值为f(e),f(g),f(i);极小值点为d,f,h,极小值为f(d),f(f),f(h).
梳理 (1)极小值点与极小值
若函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)= ,而且在点x=a附近的左侧 ,右侧 ,就把 叫做函数y=f(x)的极小值点, 叫做函数y=f(x)的极小值.
(2)极大值点与极大值
若函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)= ,而且在点x=b附近的左侧 ,右侧 ,就把 叫做函数y=f(x)的极大值点, 叫做函数y=f(x)的极大值.
(3)极大值点、极小值点统称为 ;极大值、极小值统称为 .
0
f′(x)<0
f′(x)>0
点a
f(a)
0
f′(x)>0
f′(x)<0
点b
f(b)
极值点
极值
(1)求函数y=f(x)的极值的方法
解方程f′(x)=0,当f′(x0)=0时,
①如果在x0附近的左侧函数单调递增,即f′(x)>0,在x0的右侧函数单调递减,即f′(x)<0,那么f(x0)是 ;
②如果在x0附近的左侧函数单调递减,即f′(x)<0,在x0的右侧函数单调递增,即f′(x)>0,那么f(x0)是 .
知识点二 函数极值的求法与步骤
极大值
极小值
(2)求可导函数f(x)的极值的步骤
①确定函数的定义区间,求导数f′(x);
②求方程 的根;
③列表;
④利用f′(x)与f(x)随x的变化情况表,根据极值点左右两侧单调性的变化情况求极值.
f′(x)=0
1.导数为0的点一定是极值点.( )
2.函数的极大值一定大于极小值.( )
3.函数y=f(x)一定有极大值和极小值.( )
4.极值点处的导数一定为0.( )
[思考辨析 判断正误]
×
×
×
×
题型探究
类型一 求函数的极值点和极值
命题角度1 不含参数的函数求极值
例1 求下列函数的极值.
解 函数f(x)的定义域为R.
令f′(x)=0,得x=-1或x=1.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-1) -1 (-1,1) 1 (1,+∞)
f′(x) - 0 + 0 -
f(x) ↘ 极小值 ↗ 极大值 ↘
由上表可以看出,当x=-1时,函数有极小值,且极小值为f(-1)=-3;
当x=1时,函数有极大值,且极大值为f(1)=-1.
令f′(x)=0,解得x=e.
当x变化时,f′(x)与f(x)的变化情况如下表:
x (0,e) e (e,+∞)
f′(x) + 0 -
f(x) ?↗ 极大值 ↘
反思与感悟 函数极值和极值点的求解步骤
(1)确定函数的定义域.
(2)求方程f′(x)=0的根.
(3)用方程f′(x)=0的根顺次将函数的定义域分成若干个小开区间,并列成表格.
(4)由f′(x)在方程f′(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况.
特别提醒:当实数根较多时,要充分利用表格,使极值点的确定一目了然.
解 f′(x)=x2-2x-3.
令f′(x)=0,得x1=-1,x2=3,
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-1) -1 (-1,3) 3 (3,+∞)
f′(x) + 0 - 0 +
f(x) ↗ 极大值 ?↘ 极小值 ↗
由上表可以看出,当x=-1时,函数有极大值,且极大值f(-1)=
当x=3时,函数有极小值,且极小值f(3)=-6.
跟踪训练1 求下列函数的极值点和极值.
解 函数f(x)的定义域为R.
f′(x)=2xe-x-x2e-x=x(2-x)e-x.
令f′(x)=0,得x=0或x=2.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,0) 0 (0,2) 2 (2,+∞)
f′(x) - 0 + 0 -
f(x) ↘ 极小值 ↗ 极大值 ↘
由上表可以看出,当x=0时,函数有极小值,且极小值为f(0)=0.
当x=2时,函数有极大值,且极大值为f(2)=4e-2.
(2)f(x)=x2e-x.
解 f′(x)=[x2+(a+2)x-2a2+4a]ex.
令f′(x)=0,解得x=-2a或x=a-2,
分以下两种情况讨论:
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-2a) -2a (-2a,a-2) a-2 (a-2,+∞)
f′(x) + 0 - 0 +
f(x) ↗ 极大值 ↘ 极小值 ↗
所以f(x)在(-∞,-2a),(a-2,+∞)上是增函数,在(-2a,a-2)上是减函数,函数f(x)在x=-2a处取得极大值f(-2a),且f(-2a)=3ae-2a,函数f(x)在x=a-2处取得极小值f(a-2),且f(a-2)=(4-3a)ea-2.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,a-2) a-2 (a-2,-2a) -2a (-2a,+∞)
f′(x) + 0 - 0 +
f(x) ↗ 极大值 ↘ 极小值 ↗
所以f(x)在(-∞,a-2),(-2a,+∞)上是增函数,在(a-2,-2a)上是减函数,函数f(x)在x=a-2处取得极大值f(a-2),且f(a-2)=(4-3a)ea-2,函数f(x)在x=-2a处取得极小值f(-2a),且f(-2a)=3ae-2a.
反思与感悟 讨论参数应从f′(x)=0的两根x1,x2相等与否入手进行.
跟踪训练2 已知函数f(x)=x-aln x(a∈R).
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
因而f(1)=1,f′(1)=-1.
所以曲线y=f(x)在点A(1,f(1))处的切线方程为
y-1=-(x-1),即x+y-2=0.
①当a≤0时,f′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f′(x)=0,解得x=a.
又当x∈(0,a)时,f′(x)<0,
当x∈(a,+∞)时,f′(x)>0,
从而函数f(x)在x=a处取得极小值,且极小值为f(a)=a-aln a,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
(2)求函数f(x)的极值.
例3 (1)已知函数f(x)的导数f′(x)=a(x+1)(x-a),若f(x)在x=a处取到极大值,则a的取值范围是
A.(-∞,-1) B.(0,+∞) C.(0,1) D.(-1,0)
类型二 利用函数的极值求参数
√
解析 若a<-1,因为f′(x)=a(x+1)(x-a),
所以f(x)在(-∞,a)上单调递减,在(a,-1)上单调递增,
所以f(x)在x=a处取得极小值,与题意不符;
若-1若a>0,则f(x)在(-1,a)上单调递减,在(a,+∞)上单调递增,与题意不符,故选D.
(2)已知函数f(x)=x3+3ax2+bx+a2在x=-1时有极值0,则a=____,b=____.
2
9
解析 因为f(x)在x=-1时有极值0,且f′(x)=3x2+6ax+b,
当a=1,b=3时,f′(x)=3x2+6x+3=3(x+1)2≥0,
所以f(x)在R上为增函数,无极值,故舍去.
当a=2,b=9时,f′(x)=3x2+12x+9=3(x+1)(x+3).
当x∈(-3,-1)时,f(x)为减函数,
当x∈(-1,+∞)时,f(x)为增函数,
所以f(x)在x=-1处取得极小值,因此a=2,b=9.
反思与感悟 已知函数的极值求参数时应注意两点
(1)待定系数法:常根据极值点处导数为0和极值两个条件列出方程组,用待定系数法求解.
(2)验证:因为导数值为0不一定此点就是极值点,故利用上述方程组解出的解必须验证.
解 ∵f(x)=aln x+bx2+x,
跟踪训练3 设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点.
(1)试确定常数a和b的值;
当x∈(0,1)时,f′(x)<0;当x∈(1,2)时,f′(x)>0;
当x∈(2,+∞)时,f′(x)<0.
故x=1是函数f(x)的极小值点,x=2是函数f(x)的极大值点.
(2)判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由.
达标检测
1
2
3
4
5
1.函数f(x)的定义域为R,它的导函数y=f′(x)的
部分图象如图所示,则下面结论错误的是
A.在(1,2)上函数f(x)为增函数
B.在(3,4)上函数f(x)为减函数
C.在(1,3)上函数f(x)有极大值
D.x=3是函数f(x)在区间[1,5]上的极小值点
√
解析 根据导函数图象知,x∈(1,2)时,f′(x)>0,x∈(2,4)时,f′(x)<0,x∈(4,5)时,f′(x)>0.∴f(x)在(1,2),(4,5)上为增函数,在(2,4)上为减函数,x=2是f(x)在[1,5]上的极大值点,x=4是极小值点.故选D.
1
2
3
4
5
C.x=2为f(x)的极大值点
D.x=2为f(x)的极小值点
√
1
2
3
4
5
当x∈(0,2)时,f′(x)<0,当x∈(2,+∞)时,f′(x)>0.
因为x=2为f(x)的极小值点,故选D.
3.函数f(x)=ax-1-ln x(a≤0)在定义域内的极值点的个数为____.
所以当a≤0时,f′(x)<0在(0,+∞)上恒成立,
所以函数f(x)在(0,+∞)上单调递减,
所以f(x)在(0,+∞)上没有极值点.
0
1
2
3
4
5
-2
解析 f′(x)=3x2+2ax+b,
1
2
3
4
5
1
2
3
4
5
又f(x)的定义域为(0,+∞),
令f′(x)=0,解得x=1.
当x变化时,f′(x),f(x)的变化情况如下表:
x (0,1) 1 (1,+∞)
f′(x) - 0 +
f(x) ↘ 极小值 ↗
∴f(x)的单调递减区间为(0,1),单调递增区间为(1,+∞).
1
2
3
4
5
(2)判断f(x)的单调区间,并求极值.
1.求函数极值的步骤
(1)确定函数的定义域;
(2)求导数f′(x);
(3)解方程f′(x)=0得方程的根;
(4)利用方程f′(x)=0的根将定义域分成若干个小开区间,列表,判定导函数在各个小开区间的符号;
(5)确定函数的极值,如果f′(x)的符号在x0处由正(负)变负(正),则f(x)在x0处取得极大(小)值.
规律与方法
2.已知函数极值,确定函数解析式中的参数时,注意两点
(1)根据极值点的导数为0和极值这两个条件列方程组,利用待定系数法求解;
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证充分性.
5.3.2 函数的极值与导数(一)
学习目标
1.了解函数极值的概念,会从几何方面直观理解函数的极值与导数的关系.
2.掌握函数极值的判定及求法.
3.掌握函数在某一点取得极值的条件.
问题导学
思考 观察函数y=f(x)的图象,指出其极大值点和极小值点及极值.
知识点一 函数的极值点和极值
答案 极大值点为e,g,i,极大值为f(e),f(g),f(i);极小值点为d,f,h,极小值为f(d),f(f),f(h).
梳理 (1)极小值点与极小值
若函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)= ,而且在点x=a附近的左侧 ,右侧 ,就把 叫做函数y=f(x)的极小值点, 叫做函数y=f(x)的极小值.
(2)极大值点与极大值
若函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)= ,而且在点x=b附近的左侧 ,右侧 ,就把 叫做函数y=f(x)的极大值点, 叫做函数y=f(x)的极大值.
(3)极大值点、极小值点统称为 ;极大值、极小值统称为 .
0
f′(x)<0
f′(x)>0
点a
f(a)
0
f′(x)>0
f′(x)<0
点b
f(b)
极值点
极值
(1)求函数y=f(x)的极值的方法
解方程f′(x)=0,当f′(x0)=0时,
①如果在x0附近的左侧函数单调递增,即f′(x)>0,在x0的右侧函数单调递减,即f′(x)<0,那么f(x0)是 ;
②如果在x0附近的左侧函数单调递减,即f′(x)<0,在x0的右侧函数单调递增,即f′(x)>0,那么f(x0)是 .
知识点二 函数极值的求法与步骤
极大值
极小值
(2)求可导函数f(x)的极值的步骤
①确定函数的定义区间,求导数f′(x);
②求方程 的根;
③列表;
④利用f′(x)与f(x)随x的变化情况表,根据极值点左右两侧单调性的变化情况求极值.
f′(x)=0
1.导数为0的点一定是极值点.( )
2.函数的极大值一定大于极小值.( )
3.函数y=f(x)一定有极大值和极小值.( )
4.极值点处的导数一定为0.( )
[思考辨析 判断正误]
×
×
×
×
题型探究
类型一 求函数的极值点和极值
命题角度1 不含参数的函数求极值
例1 求下列函数的极值.
解 函数f(x)的定义域为R.
令f′(x)=0,得x=-1或x=1.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-1) -1 (-1,1) 1 (1,+∞)
f′(x) - 0 + 0 -
f(x) ↘ 极小值 ↗ 极大值 ↘
由上表可以看出,当x=-1时,函数有极小值,且极小值为f(-1)=-3;
当x=1时,函数有极大值,且极大值为f(1)=-1.
令f′(x)=0,解得x=e.
当x变化时,f′(x)与f(x)的变化情况如下表:
x (0,e) e (e,+∞)
f′(x) + 0 -
f(x) ?↗ 极大值 ↘
反思与感悟 函数极值和极值点的求解步骤
(1)确定函数的定义域.
(2)求方程f′(x)=0的根.
(3)用方程f′(x)=0的根顺次将函数的定义域分成若干个小开区间,并列成表格.
(4)由f′(x)在方程f′(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况.
特别提醒:当实数根较多时,要充分利用表格,使极值点的确定一目了然.
解 f′(x)=x2-2x-3.
令f′(x)=0,得x1=-1,x2=3,
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-1) -1 (-1,3) 3 (3,+∞)
f′(x) + 0 - 0 +
f(x) ↗ 极大值 ?↘ 极小值 ↗
由上表可以看出,当x=-1时,函数有极大值,且极大值f(-1)=
当x=3时,函数有极小值,且极小值f(3)=-6.
跟踪训练1 求下列函数的极值点和极值.
解 函数f(x)的定义域为R.
f′(x)=2xe-x-x2e-x=x(2-x)e-x.
令f′(x)=0,得x=0或x=2.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,0) 0 (0,2) 2 (2,+∞)
f′(x) - 0 + 0 -
f(x) ↘ 极小值 ↗ 极大值 ↘
由上表可以看出,当x=0时,函数有极小值,且极小值为f(0)=0.
当x=2时,函数有极大值,且极大值为f(2)=4e-2.
(2)f(x)=x2e-x.
解 f′(x)=[x2+(a+2)x-2a2+4a]ex.
令f′(x)=0,解得x=-2a或x=a-2,
分以下两种情况讨论:
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-2a) -2a (-2a,a-2) a-2 (a-2,+∞)
f′(x) + 0 - 0 +
f(x) ↗ 极大值 ↘ 极小值 ↗
所以f(x)在(-∞,-2a),(a-2,+∞)上是增函数,在(-2a,a-2)上是减函数,函数f(x)在x=-2a处取得极大值f(-2a),且f(-2a)=3ae-2a,函数f(x)在x=a-2处取得极小值f(a-2),且f(a-2)=(4-3a)ea-2.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,a-2) a-2 (a-2,-2a) -2a (-2a,+∞)
f′(x) + 0 - 0 +
f(x) ↗ 极大值 ↘ 极小值 ↗
所以f(x)在(-∞,a-2),(-2a,+∞)上是增函数,在(a-2,-2a)上是减函数,函数f(x)在x=a-2处取得极大值f(a-2),且f(a-2)=(4-3a)ea-2,函数f(x)在x=-2a处取得极小值f(-2a),且f(-2a)=3ae-2a.
反思与感悟 讨论参数应从f′(x)=0的两根x1,x2相等与否入手进行.
跟踪训练2 已知函数f(x)=x-aln x(a∈R).
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
因而f(1)=1,f′(1)=-1.
所以曲线y=f(x)在点A(1,f(1))处的切线方程为
y-1=-(x-1),即x+y-2=0.
①当a≤0时,f′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f′(x)=0,解得x=a.
又当x∈(0,a)时,f′(x)<0,
当x∈(a,+∞)时,f′(x)>0,
从而函数f(x)在x=a处取得极小值,且极小值为f(a)=a-aln a,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
(2)求函数f(x)的极值.
例3 (1)已知函数f(x)的导数f′(x)=a(x+1)(x-a),若f(x)在x=a处取到极大值,则a的取值范围是
A.(-∞,-1) B.(0,+∞) C.(0,1) D.(-1,0)
类型二 利用函数的极值求参数
√
解析 若a<-1,因为f′(x)=a(x+1)(x-a),
所以f(x)在(-∞,a)上单调递减,在(a,-1)上单调递增,
所以f(x)在x=a处取得极小值,与题意不符;
若-1
(2)已知函数f(x)=x3+3ax2+bx+a2在x=-1时有极值0,则a=____,b=____.
2
9
解析 因为f(x)在x=-1时有极值0,且f′(x)=3x2+6ax+b,
当a=1,b=3时,f′(x)=3x2+6x+3=3(x+1)2≥0,
所以f(x)在R上为增函数,无极值,故舍去.
当a=2,b=9时,f′(x)=3x2+12x+9=3(x+1)(x+3).
当x∈(-3,-1)时,f(x)为减函数,
当x∈(-1,+∞)时,f(x)为增函数,
所以f(x)在x=-1处取得极小值,因此a=2,b=9.
反思与感悟 已知函数的极值求参数时应注意两点
(1)待定系数法:常根据极值点处导数为0和极值两个条件列出方程组,用待定系数法求解.
(2)验证:因为导数值为0不一定此点就是极值点,故利用上述方程组解出的解必须验证.
解 ∵f(x)=aln x+bx2+x,
跟踪训练3 设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点.
(1)试确定常数a和b的值;
当x∈(0,1)时,f′(x)<0;当x∈(1,2)时,f′(x)>0;
当x∈(2,+∞)时,f′(x)<0.
故x=1是函数f(x)的极小值点,x=2是函数f(x)的极大值点.
(2)判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由.
达标检测
1
2
3
4
5
1.函数f(x)的定义域为R,它的导函数y=f′(x)的
部分图象如图所示,则下面结论错误的是
A.在(1,2)上函数f(x)为增函数
B.在(3,4)上函数f(x)为减函数
C.在(1,3)上函数f(x)有极大值
D.x=3是函数f(x)在区间[1,5]上的极小值点
√
解析 根据导函数图象知,x∈(1,2)时,f′(x)>0,x∈(2,4)时,f′(x)<0,x∈(4,5)时,f′(x)>0.∴f(x)在(1,2),(4,5)上为增函数,在(2,4)上为减函数,x=2是f(x)在[1,5]上的极大值点,x=4是极小值点.故选D.
1
2
3
4
5
C.x=2为f(x)的极大值点
D.x=2为f(x)的极小值点
√
1
2
3
4
5
当x∈(0,2)时,f′(x)<0,当x∈(2,+∞)时,f′(x)>0.
因为x=2为f(x)的极小值点,故选D.
3.函数f(x)=ax-1-ln x(a≤0)在定义域内的极值点的个数为____.
所以当a≤0时,f′(x)<0在(0,+∞)上恒成立,
所以函数f(x)在(0,+∞)上单调递减,
所以f(x)在(0,+∞)上没有极值点.
0
1
2
3
4
5
-2
解析 f′(x)=3x2+2ax+b,
1
2
3
4
5
1
2
3
4
5
又f(x)的定义域为(0,+∞),
令f′(x)=0,解得x=1.
当x变化时,f′(x),f(x)的变化情况如下表:
x (0,1) 1 (1,+∞)
f′(x) - 0 +
f(x) ↘ 极小值 ↗
∴f(x)的单调递减区间为(0,1),单调递增区间为(1,+∞).
1
2
3
4
5
(2)判断f(x)的单调区间,并求极值.
1.求函数极值的步骤
(1)确定函数的定义域;
(2)求导数f′(x);
(3)解方程f′(x)=0得方程的根;
(4)利用方程f′(x)=0的根将定义域分成若干个小开区间,列表,判定导函数在各个小开区间的符号;
(5)确定函数的极值,如果f′(x)的符号在x0处由正(负)变负(正),则f(x)在x0处取得极大(小)值.
规律与方法
2.已知函数极值,确定函数解析式中的参数时,注意两点
(1)根据极值点的导数为0和极值这两个条件列方程组,利用待定系数法求解;
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证充分性.
