人教A版(2019)高中数学选择性必修第二册 【整合课件】5.3.2生活中的优化问题 课件(共42张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 【整合课件】5.3.2生活中的优化问题 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 14:10:05 | ||
图片预览











文档简介
(共42张PPT)
§5.4 生活中的优化问题举例
学习目标
1.了解导数在解决实际问题中的作用.
2.掌握利用导数解决简单的实际生活中的优化问题.
问题导学
(1)生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为 .
(2)利用导数解决优化问题的实质是 .
(3)解决优化问题的基本思路:
知识点 生活中的优化问题
上述解决优化问题的过程是一个典型的 过程.
优化问题
求函数最值
数学建模
1.生活中常见到的收益最高,用料最省等问题就是数学中的最大、最小值问题.( )
2.解决应用问题的关键是建立数学模型.( )
[思考辨析 判断正误]
√
√
题型探究
类型一 几何中的最值问题
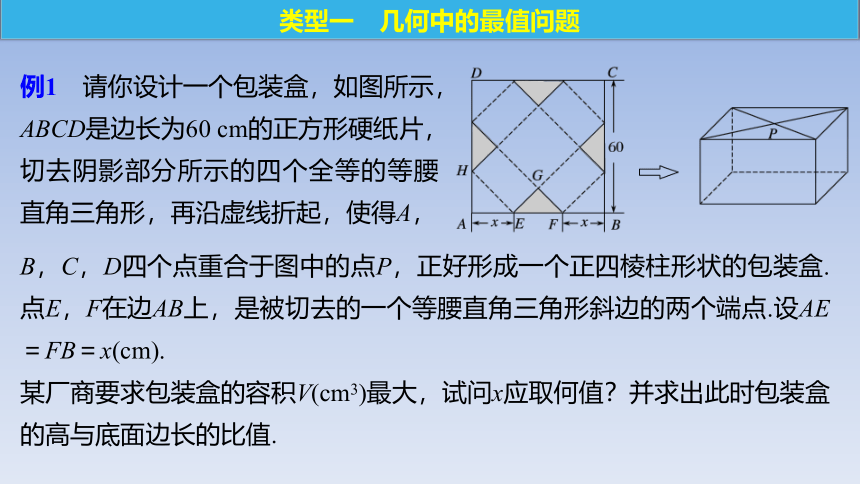
例1 请你设计一个包装盒,如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,
B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒.点E,F在边AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=x(cm).
某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
令V′(x)=0,得x=0(舍去)或x=20.
∵当00;当20∴V(x)在x=20时取极大值也是唯一的极值,故为最大值.
引申探究
本例条件不变,若要求包装盒的侧面积S(cm2)最大,试问x应取何值?
∵EF=60-2x,
=8x(30-x)=-8x2+240x
=-8(x-15)2+8×152.
∴当x=15时,S侧最大为1 800 cm2.
反思与感悟 面积、体积(容积)最大,周长最短,距离最小等实际几何问题,求解时先设出恰当的变量,将待求解最值的问题表示为变量的函数,再按函数求最值的方法求解,最后检验.
跟踪训练1 (1)已知圆柱的表面积为定值S,当圆柱的容积V最大时,圆柱的高h的值为______.
解析 设圆柱的底面半径为r,
则S圆柱底=2πr2,S圆柱侧=2πrh,
∴圆柱的表面积S=2πr2+2πrh.
令V′(r)=0,得S=6πr2,∴h=2r,
∵V′(r)只有一个极值点,
∴当h=2r时圆柱的容积最大.
(2)将一段长为100 cm的铁丝截成两段,一段弯成正方形,一段弯成圆,当正方形与圆形面积之和最小时,圆的周长为_______cm.
解析 设弯成圆的一段铁丝长为x(0设正方形与圆形的面积之和为S,
类型二 实际生活中的最值问题
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
所以商场每日销售该商品所获得的利润为
从而f′(x)=10[(x-6)2+2(x-3)(x-6)]
=30(x-4)(x-6),令f′(x)=0,得x=4或x=6.
当x变化时,f′(x),f(x)的变化情况如下表:
x (3,4) 4 (4,6)
f′(x) + 0 -
f(x) ↗ 极大值 ↘
由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点.
所以当x=4时,函数f(x)取得最大值,且最大值等于42.
答 当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
反思与感悟 解决此类有关利润的实际应用题,应灵活运用题设条件,建立利润的函数关系,常见的基本等量关系有
(1)利润=收入-成本.
(2)利润=每件产品的利润×销售件数.
解 当0(2)当年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大,并求出最大值.
解 当0当x∈(0,9)时,W′>0,当x∈(9,10)时,W′<0,
所以当x=9时,W取得最大值,
综上可得,当x=9时,W取得最大值38.6.
故当年产量为9千件时,该公司在这一品牌服装的生产中所获得的年利润最大,最大利润为38.6万元.
命题角度2 用料、费用最少问题
例3 某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下工程只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元;距离为x米的相邻两墩之间的桥面工程费用为(2+ )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.
(1)试写出y关于x的函数关系式;
解 设需新建n个桥墩,
令f′(x)=0,得 =512,所以x=64.
当0当640,f(x)在区间(64,640)上为增函数,
所以f(x)在x=64处取得最小值.
(2)当m=640米时,需新建多少个桥墩才能使y最小?
反思与感悟 (1)用料最省、成本最低问题是日常生活中常见的问题之一,解决这类问题要明确自变量的意义以及最值问题所研究的对象.正确书写函数表达式,准确求导,结合实际作答.
(2)利用导数的方法解决实际问题,当在定义区间内只有一个点使f′(x)=0时,如果函数在这点有极大(小)值,那么不与端点值比较,也可以知道在这个点取得最大(小)值.
跟踪训练3 为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式;
解 设隔热层厚度为x cm,
而建造费用为C1(x)=6x.
因此得隔热层建造费用与20年的能源消耗费用之和为
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
当00,
答 当隔热层修建5 cm厚时,总费用达到最小值为70万元.
达标检测
1
2
3
4
5
解析 原油温度的瞬时变化率为f′(x)=x2-2x=(x-1)2-1(0≤x≤5),所以当x=1时,原油温度的瞬时变化率取得最小值-1.
C.-1 D.-8
√
1
2
3
4
5
2.要做一个圆锥形漏斗,其母线长为20 cm,要使其体积最大,则高应为
√
1
2
3
4
5
解析 设圆锥的高为h cm,03.某商场从生产厂家以每件20元的价格购进一批商品.若该商品零售价定为P元,销售量为Q件,且销量Q与零售价P有如下关系:Q=8 300-170P-P2,则最大毛利润为(毛利润=销售收入-进货支出)
A.30元 B.60元
C.28 000元 D.23 000元
√
1
2
3
4
5
1
2
3
4
5
解析 毛利润为(P-20)Q,
即f(P)=(P-20)(8 300-170P-P2),
f′(P)=-3P2-300P+11 700=-3(P+130)(P-30).
令f′(P)=0,
得P=30或P=-130(舍去).
又P∈[20,+∞),
故f(P)max=f(P)极大值,
故当P=30时,毛利润最大,
所以f(P)max=f(30)=23 000(元).
4.要制作一个容积为4 m3,高为1 m的无盖长方体容器,已知底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是_____元.
160
∴当x=2时,ymin=160(元).
1
2
3
4
5
5.某商品每件成本9元,售价30元,每星期卖出432件.如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低额x(单位:元,0≤x≤21)的平方成正比.已知商品单价降低2元时,每星期多卖出24件.
(1)将一个星期的商品销售利润表示成x的函数;
解 设商品降价x元,则多卖出的商品件数为kx2.
若记商品一个星期的获利为f(x),则有
f(x)=(30-x-9)(432+kx2)=(21-x)(432+kx2).
由已知条件,得24=k×22,于是有k=6.
所以f(x)=-6x3+126x2-432x+9 072,x∈[0,21].
1
2
3
4
5
1
2
3
4
5
(2)如何定价才能使一个星期的商品销售利润最大?
解 由(1)得,f′(x)=-18x2+252x-432
=-18(x-2)(x-12).
当x变化时,f′(x),f(x)的变化情况如下表:
x [0,2) 2 (2,12) 12 (12,21]
f′(x) - 0 + 0 -
f(x) ↘ 极小值 ↗ 极大值 ↘
故当x=12时,f(x)取得极大值.
因为f(0)=9 072,f(12)=11 664.
所以定价为30-12=18(元),才能使一个星期的商品销售利润最大.
1.利用导数解决生活中优化问题的一般步骤
(1)分析实际问题中各量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系y=f(x);
(2)求函数的导数f′(x),解方程f′(x)=0;
(3)比较函数在区间端点和极值点处的函数值的大小,最大(小)者为最大(小)值.
规律与方法
2.正确理解题意,建立数学模型,利用导数求解是解答应用问题的主要思路.另外需要特别注意
(1)合理选择变量,正确写出函数解析式,给出函数定义域;
(2)与实际问题相联系;
(3)必要时注意分类讨论思想的应用.
§5.4 生活中的优化问题举例
学习目标
1.了解导数在解决实际问题中的作用.
2.掌握利用导数解决简单的实际生活中的优化问题.
问题导学
(1)生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为 .
(2)利用导数解决优化问题的实质是 .
(3)解决优化问题的基本思路:
知识点 生活中的优化问题
上述解决优化问题的过程是一个典型的 过程.
优化问题
求函数最值
数学建模
1.生活中常见到的收益最高,用料最省等问题就是数学中的最大、最小值问题.( )
2.解决应用问题的关键是建立数学模型.( )
[思考辨析 判断正误]
√
√
题型探究
类型一 几何中的最值问题
例1 请你设计一个包装盒,如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,
B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒.点E,F在边AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=x(cm).
某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
令V′(x)=0,得x=0(舍去)或x=20.
∵当0
引申探究
本例条件不变,若要求包装盒的侧面积S(cm2)最大,试问x应取何值?
∵EF=60-2x,
=8x(30-x)=-8x2+240x
=-8(x-15)2+8×152.
∴当x=15时,S侧最大为1 800 cm2.
反思与感悟 面积、体积(容积)最大,周长最短,距离最小等实际几何问题,求解时先设出恰当的变量,将待求解最值的问题表示为变量的函数,再按函数求最值的方法求解,最后检验.
跟踪训练1 (1)已知圆柱的表面积为定值S,当圆柱的容积V最大时,圆柱的高h的值为______.
解析 设圆柱的底面半径为r,
则S圆柱底=2πr2,S圆柱侧=2πrh,
∴圆柱的表面积S=2πr2+2πrh.
令V′(r)=0,得S=6πr2,∴h=2r,
∵V′(r)只有一个极值点,
∴当h=2r时圆柱的容积最大.
(2)将一段长为100 cm的铁丝截成两段,一段弯成正方形,一段弯成圆,当正方形与圆形面积之和最小时,圆的周长为_______cm.
解析 设弯成圆的一段铁丝长为x(0
类型二 实际生活中的最值问题
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
所以商场每日销售该商品所获得的利润为
从而f′(x)=10[(x-6)2+2(x-3)(x-6)]
=30(x-4)(x-6),令f′(x)=0,得x=4或x=6.
当x变化时,f′(x),f(x)的变化情况如下表:
x (3,4) 4 (4,6)
f′(x) + 0 -
f(x) ↗ 极大值 ↘
由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点.
所以当x=4时,函数f(x)取得最大值,且最大值等于42.
答 当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
反思与感悟 解决此类有关利润的实际应用题,应灵活运用题设条件,建立利润的函数关系,常见的基本等量关系有
(1)利润=收入-成本.
(2)利润=每件产品的利润×销售件数.
解 当0
解 当0
所以当x=9时,W取得最大值,
综上可得,当x=9时,W取得最大值38.6.
故当年产量为9千件时,该公司在这一品牌服装的生产中所获得的年利润最大,最大利润为38.6万元.
命题角度2 用料、费用最少问题
例3 某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下工程只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元;距离为x米的相邻两墩之间的桥面工程费用为(2+ )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.
(1)试写出y关于x的函数关系式;
解 设需新建n个桥墩,
令f′(x)=0,得 =512,所以x=64.
当0
所以f(x)在x=64处取得最小值.
(2)当m=640米时,需新建多少个桥墩才能使y最小?
反思与感悟 (1)用料最省、成本最低问题是日常生活中常见的问题之一,解决这类问题要明确自变量的意义以及最值问题所研究的对象.正确书写函数表达式,准确求导,结合实际作答.
(2)利用导数的方法解决实际问题,当在定义区间内只有一个点使f′(x)=0时,如果函数在这点有极大(小)值,那么不与端点值比较,也可以知道在这个点取得最大(小)值.
跟踪训练3 为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式;
解 设隔热层厚度为x cm,
而建造费用为C1(x)=6x.
因此得隔热层建造费用与20年的能源消耗费用之和为
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
当0
答 当隔热层修建5 cm厚时,总费用达到最小值为70万元.
达标检测
1
2
3
4
5
解析 原油温度的瞬时变化率为f′(x)=x2-2x=(x-1)2-1(0≤x≤5),所以当x=1时,原油温度的瞬时变化率取得最小值-1.
C.-1 D.-8
√
1
2
3
4
5
2.要做一个圆锥形漏斗,其母线长为20 cm,要使其体积最大,则高应为
√
1
2
3
4
5
解析 设圆锥的高为h cm,0
A.30元 B.60元
C.28 000元 D.23 000元
√
1
2
3
4
5
1
2
3
4
5
解析 毛利润为(P-20)Q,
即f(P)=(P-20)(8 300-170P-P2),
f′(P)=-3P2-300P+11 700=-3(P+130)(P-30).
令f′(P)=0,
得P=30或P=-130(舍去).
又P∈[20,+∞),
故f(P)max=f(P)极大值,
故当P=30时,毛利润最大,
所以f(P)max=f(30)=23 000(元).
4.要制作一个容积为4 m3,高为1 m的无盖长方体容器,已知底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是_____元.
160
∴当x=2时,ymin=160(元).
1
2
3
4
5
5.某商品每件成本9元,售价30元,每星期卖出432件.如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低额x(单位:元,0≤x≤21)的平方成正比.已知商品单价降低2元时,每星期多卖出24件.
(1)将一个星期的商品销售利润表示成x的函数;
解 设商品降价x元,则多卖出的商品件数为kx2.
若记商品一个星期的获利为f(x),则有
f(x)=(30-x-9)(432+kx2)=(21-x)(432+kx2).
由已知条件,得24=k×22,于是有k=6.
所以f(x)=-6x3+126x2-432x+9 072,x∈[0,21].
1
2
3
4
5
1
2
3
4
5
(2)如何定价才能使一个星期的商品销售利润最大?
解 由(1)得,f′(x)=-18x2+252x-432
=-18(x-2)(x-12).
当x变化时,f′(x),f(x)的变化情况如下表:
x [0,2) 2 (2,12) 12 (12,21]
f′(x) - 0 + 0 -
f(x) ↘ 极小值 ↗ 极大值 ↘
故当x=12时,f(x)取得极大值.
因为f(0)=9 072,f(12)=11 664.
所以定价为30-12=18(元),才能使一个星期的商品销售利润最大.
1.利用导数解决生活中优化问题的一般步骤
(1)分析实际问题中各量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系y=f(x);
(2)求函数的导数f′(x),解方程f′(x)=0;
(3)比较函数在区间端点和极值点处的函数值的大小,最大(小)者为最大(小)值.
规律与方法
2.正确理解题意,建立数学模型,利用导数求解是解答应用问题的主要思路.另外需要特别注意
(1)合理选择变量,正确写出函数解析式,给出函数定义域;
(2)与实际问题相联系;
(3)必要时注意分类讨论思想的应用.
