人教A版(2019)高中数学选择性必修第二册 5.3.1《函数的极值与最大(小)值》教学设计
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 5.3.1《函数的极值与最大(小)值》教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 00:00:00 | ||
图片预览




文档简介
《函数的极值与最大(小)值》教学设计
一、创设情境,导入新课
如图(1)所示,在群山之中,各个山峰的顶端虽然不一定是群山的最高处,但它却是其附近的最高点.同样,各个谷底虽然不一定是群山之中的最低处,但它却是其附近的最低点.
师:观察图(2)中函数的图象,指出其中是否有类似山峰、山谷的地方.如果有,尝试用数学语言描述.
生:从图中可以看出,函数在这三处对应的函数值,都是其附近的函数值中的最大者;在这两处对应的函数值,都是其附近的函数值中的最小者.
设计意图:
通过群山山峰与山谷的图片,激发学生学习的兴趣,引入新知.
二、新知探究
1.合作探究1
师:观察下图,处的点的导数值是多少 此点附近的图象有什么特点 相应地,此点附近的导数的符号有什么变化规律
生:函数在点的函数值比它在点附近其他点的函数值都大,;而且在点附近的左侧,右侧.
师:下图中处的点的导数值是多少 此点附近的图象有什么特点 相应地,此点附近的导数的符号有什么变化规律
生:函数在点的函数值比它在点附近其他点的函数值都小,;而且在点附近的左侧,右侧.
2.概念生成
若函数在点的函数值比它在点附近其他点的函数值都小,;而且在点附近的左侧,右侧.我们把叫做函数的极小值点,叫做函数的极小值.
类似地,若函数在点的函数值比它在点附近其他点的函数值都大,;而且在点附近的左侧,右侧.我们把叫做函数的极大值点,叫做函数的极大值.
极小值点、极大值点统称为极值点,极小值和极大值统称为极值.
极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
设计意图:
通过具体问题的思考和分析,归纳总结出函数极值的概念,发展学生的数学抽象和数学建模核心素养.
师:如果,那么一定是极值点吗
生:不一定.
师:若,则.则,那么是极值点吗 为什么
生:不是,因为,所以单调递增.
师:函数在一点的导数值为0是函数在这点取极值的必要而不充分条件.
师:极大值一定比极小值大吗
生:极大值与极小值之间无确定的大小关系,即一个函数的极大值不一定大于极小值.
师:你能举个例子吗
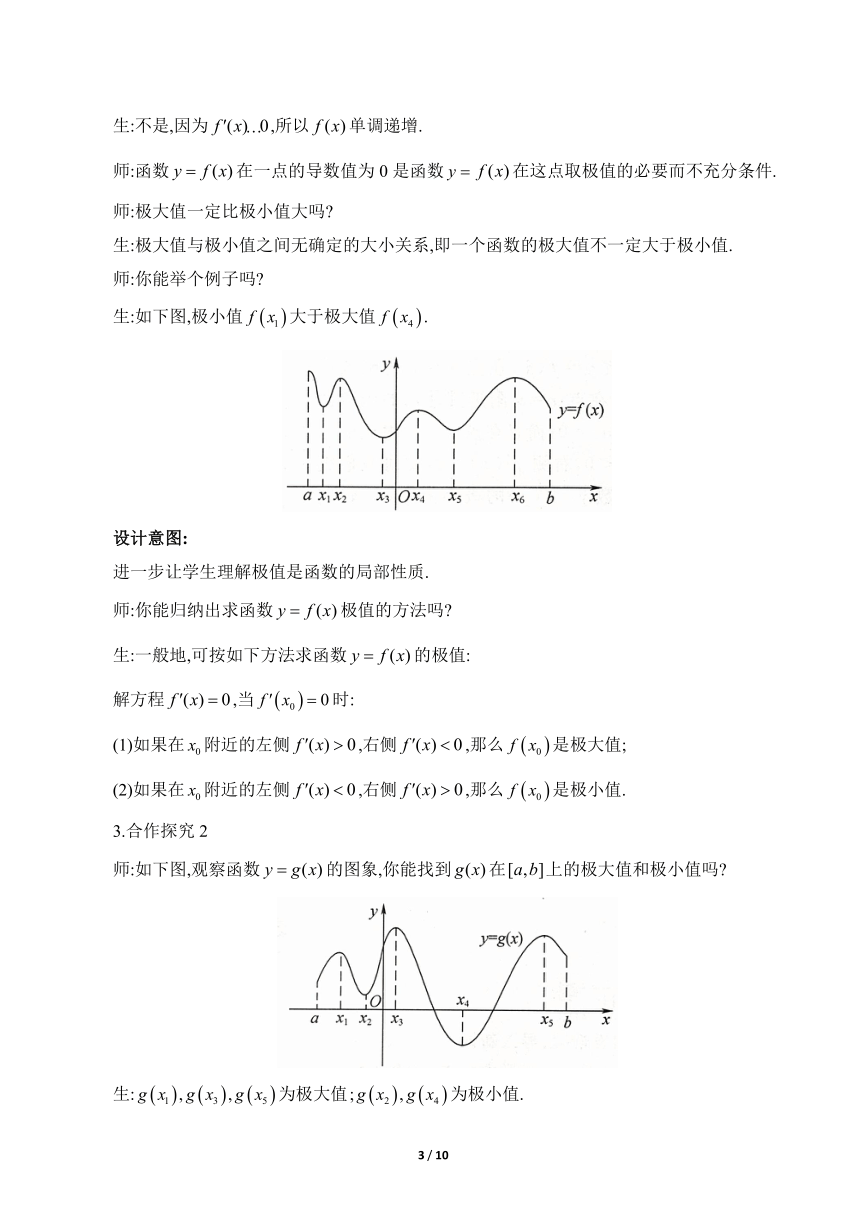
生:如下图,极小值大于极大值.
设计意图:
进一步让学生理解极值是函数的局部性质.
师:你能归纳出求函数极值的方法吗
生:一般地,可按如下方法求函数的极值:
解方程,当时:
(1)如果在附近的左侧,右侧,那么是极大值;
(2)如果在附近的左侧,右侧,那么是极小值.
3.合作探究2
师:如下图,观察函数的图象,你能找到在上的极大值和极小值吗
生:为极大值为极小值.
师:那么函数在上的最大值、最小值呢
生:为最大值,为最小值.
师:函数的极值与最值的区别是什么
生:函数的最大值和最小值是一个整体性概念.最大(小)值是通过比较整个定义域内的函数值得出的,而函数的极值是比较极值点附近的函数值得出的.函数的极值可以有多个,但最大(小)值最多只能有一个(也可能不存在).极值只能在区间内取得,而最值则可以在端点处取得.有极值的函数未必有最值,有最值的函数未必有极值.函数的极值有可能成为最值,函数的最值只要不在端点处取得必定是极值.
设计意图:
进一步让学生理解函数的极值,理清函数极值与最值间的关系.
4.形成结论
(1)函数的最大(小)值的存在性
一般地,如果在区间上函数的图象是一条连续不断的曲线,那么它必有最大值与最小值.
(2)求函数在区间上的最大值与最小值的步骤如下:
①求函数在区间上的极值;
②将函数的各极值与端点处的函数值比较,其中最大的一个是最大值,最小的一个是最小值.
三、例题剖析
例1 求下列函数的极值:
(1);
(2).
师:哪位同学完成了这两道题 (找两名学生板演)
解:(1)依题意得.
令,即,解得.
当变化时,的变化情况如下表:
所以,当时,函数有极大值,且极大值为;
当时,函数有极小值,且极小值为.
(2).
令,即,
解得.
当变化时,与的变化情况如下表:
所以,不是的极值点;
是的极大值点,并且极大值为;
是的极小值点,并且极小值为.
设计意图:
熟练掌握利用导数求函数极值的方法步骤,培养学生的数学运算核心素养.
例2 求下列各函数的最值:
(1);
(2).
解:(1),
令,得或.
当变化时,变化情况如下表:
从表中可以看出,当或时,函数在区间上取得最小值;
当或时,函数在区间上取得最大值11.
(2),令,得.
又因为,所以.
所以,所以,
所以函数在上的两个极值分别为
.
又.
比较以上函数值可得当时,,.
设计意图:通过例题的讲解,帮助学生掌握利用导数求函数最值的解题要领.
例3 若关于的三次方程有三个根,试求实数的取值范围.
解:三次方程可化为.
原方程有3个根可转化为函数的图像与直线有3个交点.
因为,
所以.
令,得或.
当变化时,的变化情况如下表:
因此,当时,有极大值,并且极大值为;
当时,有极小值,并且极小值为.
所以的图象经过特殊点.且当时,;当时,.
由上述讨论可知,函数的大致图象如图所示.
由上图可知,当时,的图象与直线有3个交点.
故当时,关于的三次方程有3个根.
完成例3后,教师引导学生归纳出画函数的大致图象的一般步骤:
(1)求出函数的定义域;
(2)求导数及函数的零点;
(3)用的零点将的定义域划分为若干个区间,列表给出在各区间上的正负,并得出的单调性与极值;
(4)确定的图象所经过的一些特殊点,以及图象的变化趋势;
(5)画出的大致图象.
设计意图:
通过此例题掌握画函数的大致图象的方法.
例4 某制造商制造并出售球形瓶装的某种饮料.瓶子的制造成本是分,其中(单位:)是瓶子的半径.已知每出售的饮料,制造商可获利分,且制造商能制作的瓶子的最大半径为.
(1)瓶子半径多大时,能使每瓶饮料的利润最大
(2)瓶子半径多大时,每瓶饮料的利润最小
解:由题意可知,每瓶饮料的利润是
.
所以.
令,解得.
当时,;当时,.
因此,当半径时,单调递增,即半径越大,利润越高;当半径时,单调递减,即半径越大,利润越低.
(1)半径为时,利润最大.
(2)半径时,利润最小,这时,表示此种瓶内饮料的利润还不够瓶子的成本,此时利润是负值.
设计意图:
通过例题的解决,体会数学建模在实际生活中的应用,增强学生的数学应用意识,发展学生的数学建模核心素养.
四、课堂小结
对于本节内容,应着重掌握函数极值的概念及利用导数求函数极值、最值的一般步骤,并学会利用导数研究生活中的最优化问题.
五、布置作业
教材第98页习题第题.
板书设计:
函数的极值与最大(小)值 一、创设情境,导入新课 二、新知探究 1.极值的概念 若函数在点的函数值比它在点附近其他点的函数值都小,;而且在点附近的左侧,右侧.我们把叫做函数的极小值点,叫做函数的极小值. 类似地,若函数在点的函数值比它在点附近其他点的函数值都大,;而且在点附近的左侧,右侧.我们把叫做函数的极大值点,叫做函数的极大值. 极小值点、极大值点统称为极值点,极小值和极大值统称为极值 2.求函数的极值的方法 解方程,当时: (1)如果在附近的左侧,右侧0,那么是极大值; (2)如果在附近的左侧,右侧0,那么是极小值 3.求函数在区间上的最值的步骤 (1)求函数在区间上的极值; (2)将函数的各极值与端点处的函数值比较,其中最大的一个是最大值,最小的一个是最小值 三、例题剖析 例1 例2 例3 画函数的大致图象的一般步骤: (1)求出函数的定义域; (2)求导数及函数的零点; (3)用的零点将的定义域划分为若干个区间,列表给出在各区间上的正负,并得出的单调性与极值; (4)确定的图象所经过的一些特殊点,以及图象的变化趋势; (5)画出的大致图象 例4 四、课堂小结 五、布置作业
1 / 10
一、创设情境,导入新课
如图(1)所示,在群山之中,各个山峰的顶端虽然不一定是群山的最高处,但它却是其附近的最高点.同样,各个谷底虽然不一定是群山之中的最低处,但它却是其附近的最低点.
师:观察图(2)中函数的图象,指出其中是否有类似山峰、山谷的地方.如果有,尝试用数学语言描述.
生:从图中可以看出,函数在这三处对应的函数值,都是其附近的函数值中的最大者;在这两处对应的函数值,都是其附近的函数值中的最小者.
设计意图:
通过群山山峰与山谷的图片,激发学生学习的兴趣,引入新知.
二、新知探究
1.合作探究1
师:观察下图,处的点的导数值是多少 此点附近的图象有什么特点 相应地,此点附近的导数的符号有什么变化规律
生:函数在点的函数值比它在点附近其他点的函数值都大,;而且在点附近的左侧,右侧.
师:下图中处的点的导数值是多少 此点附近的图象有什么特点 相应地,此点附近的导数的符号有什么变化规律
生:函数在点的函数值比它在点附近其他点的函数值都小,;而且在点附近的左侧,右侧.
2.概念生成
若函数在点的函数值比它在点附近其他点的函数值都小,;而且在点附近的左侧,右侧.我们把叫做函数的极小值点,叫做函数的极小值.
类似地,若函数在点的函数值比它在点附近其他点的函数值都大,;而且在点附近的左侧,右侧.我们把叫做函数的极大值点,叫做函数的极大值.
极小值点、极大值点统称为极值点,极小值和极大值统称为极值.
极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
设计意图:
通过具体问题的思考和分析,归纳总结出函数极值的概念,发展学生的数学抽象和数学建模核心素养.
师:如果,那么一定是极值点吗
生:不一定.
师:若,则.则,那么是极值点吗 为什么
生:不是,因为,所以单调递增.
师:函数在一点的导数值为0是函数在这点取极值的必要而不充分条件.
师:极大值一定比极小值大吗
生:极大值与极小值之间无确定的大小关系,即一个函数的极大值不一定大于极小值.
师:你能举个例子吗
生:如下图,极小值大于极大值.
设计意图:
进一步让学生理解极值是函数的局部性质.
师:你能归纳出求函数极值的方法吗
生:一般地,可按如下方法求函数的极值:
解方程,当时:
(1)如果在附近的左侧,右侧,那么是极大值;
(2)如果在附近的左侧,右侧,那么是极小值.
3.合作探究2
师:如下图,观察函数的图象,你能找到在上的极大值和极小值吗
生:为极大值为极小值.
师:那么函数在上的最大值、最小值呢
生:为最大值,为最小值.
师:函数的极值与最值的区别是什么
生:函数的最大值和最小值是一个整体性概念.最大(小)值是通过比较整个定义域内的函数值得出的,而函数的极值是比较极值点附近的函数值得出的.函数的极值可以有多个,但最大(小)值最多只能有一个(也可能不存在).极值只能在区间内取得,而最值则可以在端点处取得.有极值的函数未必有最值,有最值的函数未必有极值.函数的极值有可能成为最值,函数的最值只要不在端点处取得必定是极值.
设计意图:
进一步让学生理解函数的极值,理清函数极值与最值间的关系.
4.形成结论
(1)函数的最大(小)值的存在性
一般地,如果在区间上函数的图象是一条连续不断的曲线,那么它必有最大值与最小值.
(2)求函数在区间上的最大值与最小值的步骤如下:
①求函数在区间上的极值;
②将函数的各极值与端点处的函数值比较,其中最大的一个是最大值,最小的一个是最小值.
三、例题剖析
例1 求下列函数的极值:
(1);
(2).
师:哪位同学完成了这两道题 (找两名学生板演)
解:(1)依题意得.
令,即,解得.
当变化时,的变化情况如下表:
所以,当时,函数有极大值,且极大值为;
当时,函数有极小值,且极小值为.
(2).
令,即,
解得.
当变化时,与的变化情况如下表:
所以,不是的极值点;
是的极大值点,并且极大值为;
是的极小值点,并且极小值为.
设计意图:
熟练掌握利用导数求函数极值的方法步骤,培养学生的数学运算核心素养.
例2 求下列各函数的最值:
(1);
(2).
解:(1),
令,得或.
当变化时,变化情况如下表:
从表中可以看出,当或时,函数在区间上取得最小值;
当或时,函数在区间上取得最大值11.
(2),令,得.
又因为,所以.
所以,所以,
所以函数在上的两个极值分别为
.
又.
比较以上函数值可得当时,,.
设计意图:通过例题的讲解,帮助学生掌握利用导数求函数最值的解题要领.
例3 若关于的三次方程有三个根,试求实数的取值范围.
解:三次方程可化为.
原方程有3个根可转化为函数的图像与直线有3个交点.
因为,
所以.
令,得或.
当变化时,的变化情况如下表:
因此,当时,有极大值,并且极大值为;
当时,有极小值,并且极小值为.
所以的图象经过特殊点.且当时,;当时,.
由上述讨论可知,函数的大致图象如图所示.
由上图可知,当时,的图象与直线有3个交点.
故当时,关于的三次方程有3个根.
完成例3后,教师引导学生归纳出画函数的大致图象的一般步骤:
(1)求出函数的定义域;
(2)求导数及函数的零点;
(3)用的零点将的定义域划分为若干个区间,列表给出在各区间上的正负,并得出的单调性与极值;
(4)确定的图象所经过的一些特殊点,以及图象的变化趋势;
(5)画出的大致图象.
设计意图:
通过此例题掌握画函数的大致图象的方法.
例4 某制造商制造并出售球形瓶装的某种饮料.瓶子的制造成本是分,其中(单位:)是瓶子的半径.已知每出售的饮料,制造商可获利分,且制造商能制作的瓶子的最大半径为.
(1)瓶子半径多大时,能使每瓶饮料的利润最大
(2)瓶子半径多大时,每瓶饮料的利润最小
解:由题意可知,每瓶饮料的利润是
.
所以.
令,解得.
当时,;当时,.
因此,当半径时,单调递增,即半径越大,利润越高;当半径时,单调递减,即半径越大,利润越低.
(1)半径为时,利润最大.
(2)半径时,利润最小,这时,表示此种瓶内饮料的利润还不够瓶子的成本,此时利润是负值.
设计意图:
通过例题的解决,体会数学建模在实际生活中的应用,增强学生的数学应用意识,发展学生的数学建模核心素养.
四、课堂小结
对于本节内容,应着重掌握函数极值的概念及利用导数求函数极值、最值的一般步骤,并学会利用导数研究生活中的最优化问题.
五、布置作业
教材第98页习题第题.
板书设计:
函数的极值与最大(小)值 一、创设情境,导入新课 二、新知探究 1.极值的概念 若函数在点的函数值比它在点附近其他点的函数值都小,;而且在点附近的左侧,右侧.我们把叫做函数的极小值点,叫做函数的极小值. 类似地,若函数在点的函数值比它在点附近其他点的函数值都大,;而且在点附近的左侧,右侧.我们把叫做函数的极大值点,叫做函数的极大值. 极小值点、极大值点统称为极值点,极小值和极大值统称为极值 2.求函数的极值的方法 解方程,当时: (1)如果在附近的左侧,右侧0,那么是极大值; (2)如果在附近的左侧,右侧0,那么是极小值 3.求函数在区间上的最值的步骤 (1)求函数在区间上的极值; (2)将函数的各极值与端点处的函数值比较,其中最大的一个是最大值,最小的一个是最小值 三、例题剖析 例1 例2 例3 画函数的大致图象的一般步骤: (1)求出函数的定义域; (2)求导数及函数的零点; (3)用的零点将的定义域划分为若干个区间,列表给出在各区间上的正负,并得出的单调性与极值; (4)确定的图象所经过的一些特殊点,以及图象的变化趋势; (5)画出的大致图象 例4 四、课堂小结 五、布置作业
1 / 10
