人教A版(2019)数学选择性必修二册5.1.2导数的概念及其几何意义 导学案(含答案)
文档属性
| 名称 | 人教A版(2019)数学选择性必修二册5.1.2导数的概念及其几何意义 导学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 181.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 14:43:39 | ||
图片预览




文档简介
5.1.2 导数的概念及其几何意义
【学习目标】
1. 经历由平均变化率到瞬时变化率的过程,体会导数的概念的实际背景.
2. 了解导函数的概念,理解导数的几何意义.
3.根据导数的几何意义,会求曲线上某点处的切线方程.
4.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.
【学习过程】
一、课前预习
预习课本P64~69,思考并完成以下问题
(1)导数的几何意义是什么?
(2)导函数的概念是什么?怎样求导函数?
(3)怎么求过一点的曲线的切线方程?
二、课前小测
1.判断正误(正确的打“√”,错误的打“×”)
(1)函数y=f (x)在x=x0处的导数即为在该点处的斜率,也就是k=f ′(x0). ( )
(2)f ′(x1)>f ′(x2)反映了曲线在x=x1处比在x=x2处瞬时变化率较大. ( )
(3)f ′(x0)就是导函数y=f ′(x)在x0处的函数值. ( )
(4)若f ′(x0)=0,则曲线在x=x0处切线不存在. ( )
2.若曲线y=f (x)在点(x0,f (x0))处的切线方程为2x+y+1=0,则( )
A.f ′(x0)>0 B.f ′(x0)=0
C.f ′(x0)<0 D.f ′(x0)不存在
3.(教材P70习题T6改编)函数y=f (x)的图象如图所示,下列描述错误的是( )
A.x=-5处比x=-2处变化快
B.x=-4处呈上升趋势
C.x=1和x=2处增减趋势相反
D.x=0处呈上升趋势
4.已知函数f (x)在x0处的导数为f ′(x0)=1,则函数f (x)在x0处切线的倾斜角为________.
5.若函数f (x)在点A(1,2)处的导数是-1,那么过点A的切线方程是________.
三、新知探究
1.导数的概念
如果当Δx→0时,平均变化率无限趋近于一个确定的值,即有极限,则称y=f (x)在x=x0处可导,并把这个确定的值叫做y=f (x)在x=x0处的导数(也称为瞬时变化率),记作f ′(x0)或,即f ′(x0)= = .
思考:f ′(x0)>0和f ′(x0)<0反映了怎样的意义?
[提示] f ′(x0)>0反映了瞬时变化率呈增长趋势,
f ′(x0)<0反映了瞬时变化率呈下降趋势.
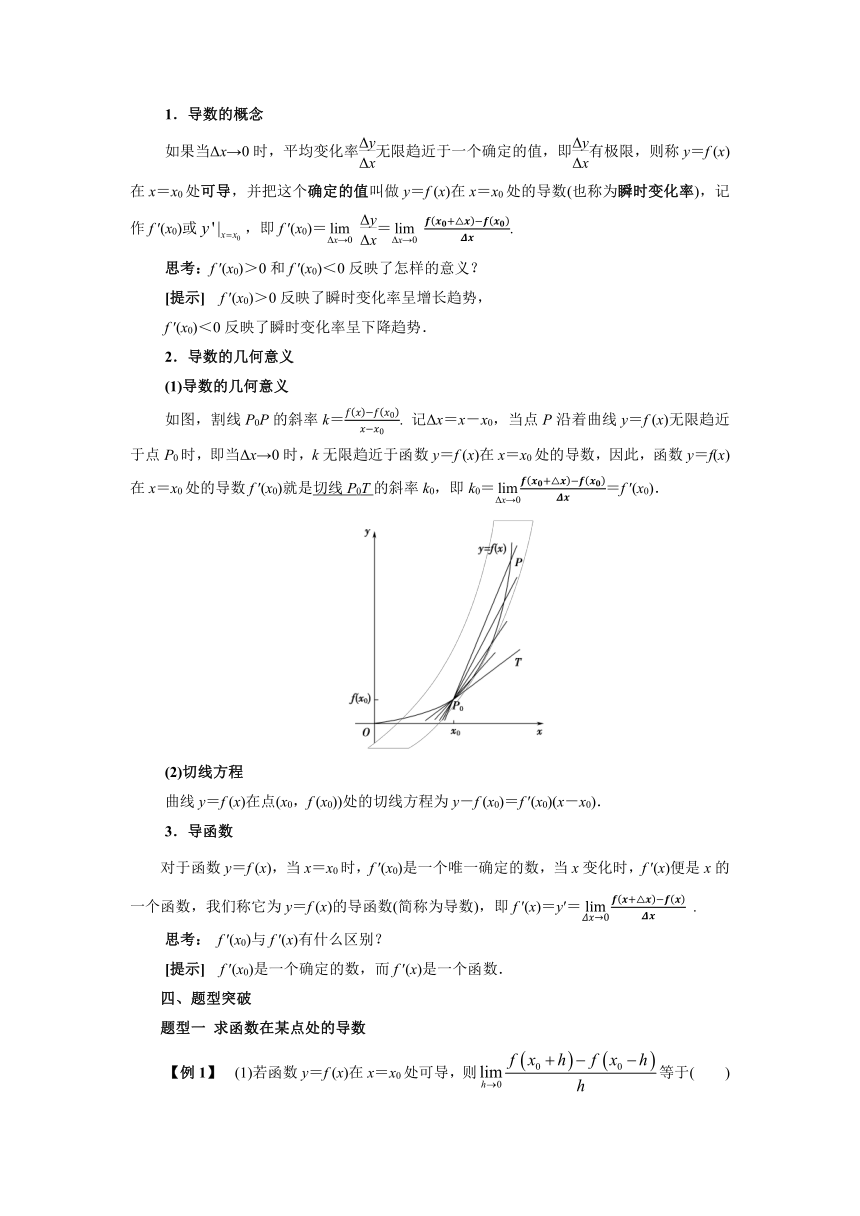
2.导数的几何意义
(1)导数的几何意义
如图,割线P0P的斜率k=. 记Δx=x-x0,当点P沿着曲线y=f (x)无限趋近于点P0时,即当Δx→0时,k无限趋近于函数y=f (x)在x=x0处的导数,因此,函数y=f(x)在x=x0处的导数f ′(x0)就是切线P0T的斜率k0,即k0==f ′(x0).
(2)切线方程
曲线y=f (x)在点(x0,f (x0))处的切线方程为y-f (x0)=f ′(x0)(x-x0).
3.导函数
对于函数y=f (x),当x=x0时,f ′(x0)是一个唯一确定的数,当x变化时,f ′(x)便是x的一个函数,我们称它为y=f (x)的导函数(简称为导数),即f ′(x)=y′= .
思考: f ′(x0)与f ′(x)有什么区别?
[提示] f ′(x0)是一个确定的数,而f ′(x)是一个函数.
四、题型突破
题型一 求函数在某点处的导数
【例1】 (1)若函数y=f (x)在x=x0处可导,则等于( )
A.f ′(x0) B.2f ′(x0) C.-2f ′(x0) D.0
(2)求函数y=3x2在x=1处的导数.
【反思感悟】
利用导数定义求导数
1 取极限前,要注意化简,保证使Δx→0时分母不为0.
2 函数在x0处的导数f ′ x0 只与x0有关,与Δx无关.
3 导数可以描述事物的瞬时变化率,应用非常广泛.
【跟踪训练】
1.建造一栋面积为x m2的房屋需要成本y万元,y是x的函数,y=f (x)=++0.3,求f ′(100),并解释它的实际意义.
题型二 导数几何意义的应用
【例2】 (1)已知函数y=f (x)的图象如图所示,则其导函数y=f ′(x)的图象可能是( )
A B C D
(2)某家电制造集团为尽快实现家电下乡提出四种运输方案,据预测,这四种方案均能在规定时间T内完成预期的运输任务Q0,各种方案的运输总量Q与时间t的函数关系如下所示.在这四种方案中,运输效率(单位时间内的运输量)逐步提高的是( )
A B C D
[思路探究] (1)切线斜率大于零,则f ′(x)>0;切线斜率小于零,则f ′(x)<0;
(2)要明确运输效率的含义,题设中已经给出运输效率即单位时间内的运输量,因此,运输效率逐步提高就是指Q′(t)不断增大.
【反思感悟】
导数几何意义理解中的两个关键
关键点一:y=f x 在点x=x0处的切线斜率为k,则k>0 f ′ x0 >0;k<0 f ′ x0 <0;k=0 f ′ x0 =0.
关键点二:|f ′ x0 |越大 在x0处瞬时变化越快;|f ′ x0 |越小 在x0处瞬时变化越慢.
【跟踪训练】
2.(1)已知y=f (x)的图象如图所示,则f ′(xA)与f ′(xB)的大小关系是( )
A.f ′(xA)>f ′(xB) B.f ′(xA)<f ′(xB)
C.f ′(xA)=f ′(xB) D.不能确定
(2)若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则( )
A.a=1,b=1 B.a=-1,b=1
C.a=1,b=-1 D.a=-1,b=-1
题型三 求切线方程
[探究问题]
1.如何求曲线f (x)在点(x0,f (x0))处的切线方程?
[提示] y-y0=k(x-x0).即根据导数的几何意义,求出函数y=f (x)在点(x0,f (x0))处的导数,即曲线在该点处的切线的斜率,再由直线方程的点斜式求出切线方程.
2.曲线f (x)在点(x0,f (x0))处的切线与曲线过点(x0,y0)的切线有什么不同?
[提示] 曲线f (x)在点(x0,f (x0))处的切线,点(x0,f (x0))一定是切点,只要求出k=f ′(x0),利用点斜式写出切线方程即可;而曲线f (x)过某点(x0,y0)的切线,给出的点(x0,y0)不一定在曲线上,即使在曲线上也不一定是切点.
3.曲线在某点处的切线是否与曲线只有一个交点?
[提示] 不一定.曲线y=f (x)在点P(x0,y0)处的切线l与曲线y=f (x)的交点个数不一定只有一个,如图所示.
【例3】 已知曲线C:y=x3.
(1)求曲线C在横坐标为x=1的点处的切线方程;
(2)求曲线C过点(1,1)的切线方程.
【多维探究】
1.把题中条件“y=x3”改成“y=x2”,求曲线在x=1点处的切线方程
2.求曲线y=x2+1过点P(1,0)的切线方程.
【反思感悟】
利用导数的几何意义求切线方程的方法
(1)若已知点(x0,y0)在已知曲线上,求在点(x0,y0)处的切线方程,先求出函数y=f (x)在点x0处的导数,然后根据直线的点斜式方程,得切线方程y-y0=f ′(x0)(x-x0).
(2)若点(x0,y0)不在曲线上,求过点(x0,y0)的切线方程,首先应设出切点坐标,然后根据导数的几何意义列出等式,求出切点坐标,进而求出切线方程.
五、达标检测
1.下面说法正确的是( )
A.若f ′(x0)不存在,则曲线y=f (x)在点(x0,f (x0))处没有切线
B.若曲线y=f (x)在点(x0,f (x0))处有切线,则f ′(x0)必存在
C.若f ′(x0)不存在,则曲线y=f (x)在点(x0,f (x0))处的切线斜率不存在
D.若曲线y=f (x)在点(x0,f (x0))处没有切线,则f ′(x0)有可能存在
2.已知函数y=f (x)是可导函数,且f ′(1)=2,则 =( )
A. B.2 C.1 D.-1
3.设曲线f (x)=ax2在点(1,a)处的切线与直线2x-y-6=0平行,则a等于( )
A.1 B. C.- D.-1
4.曲线f (x)=在点(-2,-1)处的切线方程为________.
5.已知曲线y=2x2-7在点P处的切线方程为8x-y-15=0,求切点P的坐标.
六、本课小结
1.函数f (x)在x=x0处的导数f ′(x0)=0并不能说明函数图象的上升与下降发生了转变,若函数在x=x0左右的导数都大于0,或者都小于0,则函数图象的走势并没有发生转变.如函数f (x)=x3在x=0处的导数等于0,但f (x)=x3的图象一直上升.
2.求切线方程时,不仅要检验已知点是否在曲线上,还要注意对“在”和“过”的理解.
(1)若“在”,则该点为切点.
(2)若“过”,则该点不一定是切点;若“过”曲线外的一点,则该点一定不是切点.
3.曲线在某点处切线斜率的大小反映了曲线在相应点处的变化情况,由切线的倾斜程度,可以判断出曲线升降的快慢.
参考答案
课前小测
1.答案:(1)√ (2)× (3)√ (4)×
提示:(1)根据导数的几何意义知正确.
(2)若|f (x0)|越大,瞬时变化率越大,故错误.
(3)根据导函数的定义知正确.
(4)若f ′(x0)=0说明曲线在x=x0处切线平行于x轴,不能说不存在.
2.答案:C
解析:由题意可知,f ′(x0)=-2<0,故选C.
3.答案:D
解析:根据导数的几何意义:f ′(-5)>0,f ′(-4)>0,f ′(-2)=0,f ′(0)<0,f ′(1)f ′(2)<0,故D错误,故选D.
4.答案:45°
设切线的倾斜角为α,则
tan α=f ′(x0) =1,又α∈[0°,180°),
∴α=45°.
5.答案:x+y-3=0
解析:切线的斜率为k=-1.
∴点 A(1,2)处的切线方程为y-2=-(x-1),
即x+y-3=0.
题型突破
【例1】(1)答案:B
解析:∵Δx=(x0+h)-(x0-h)=2h.
∴=2=2f ′(x0).故选B.
(2)解:∵Δy=f (1+Δx)-f (1)=3(1+Δx)2-3=6Δx+3(Δx)2,∴=6+3Δx,
∴f ′(1)= = (6+3Δx)=6.
【跟踪训练】
1.解:根据导数的定义,得f ′(100)= =
=
=
=
=+
=0.105.
f ′(100)=0.105表示当建筑面积为100 m2时,成本增加的速度为1 050元/m2.
【例2】答案:(1)B (2)B
解析:(1)由y=f (x)的图象及导数的几何意义可知,当x<0时,f ′(x)>0;当x=0时,f ′(x)=0;当x>0时,f ′(x)<0,故B符合.
(2)从函数图象上看,要求图象在[0,T]上越来越陡峭,在各选项中,只有B项中图象的切线斜率在不断增大,即运输效率(单位时间内的运输量)逐步提高.故选B.
【跟踪训练】
2.答案:(1)B (2)A
解析:(1)由导数的几何意义,f ′(xA),f ′(xB)分别是切线在点A、B处切线的斜率,由图象可知f ′(xA)<f ′(xB).
(2)由题意,知k=y′|x=0
= =1,∴a=1.
又点(0,b)在切线上,∴b=1,故选A.
【例3】解:(1)将x=1代入曲线C的方程得y=1,∴切点P(1,1).
y′|x=1= =
= [3+3Δx+(Δx)2]=3.
∴k=y′|x=1=3.
∴曲线在点P(1,1)处的切线方程为y-1=3(x-1),即3x-y-2=0.
(2)设切点为Q(x0,y0),由(1)可知=3x,由题意可知kPQ=,
即=3x,又y0=x,所以=3x,即2x-3x+1=0,解得x0=1或x0=-.
①当x0=1时,切点坐标为(1,1),相应的切线方程为3x-y-2=0.
②当x0=-时,切点坐标为,相应的切线方程为y+=,即3x-4y+1=0.
【多维探究】
1.解:把x=1代入y=x2得y=12=1.即切点P(1,1),
y′|x=1= =
= (Δx+2)=2,
∴k=y′|x=1=2.
∴曲线y=x2在P(1,1)处的切线方程为y-1=2(x-1),即2x-y-1=0.
2.解:设切点为Q,
k= = (2a+Δx)=2a.
∴在Q点处的切线方程为y-(a2+1)=2a(x-a). (*)
把点(1,0)代入(*)式得-(a2+1)=2a(1-a).
解的a=1±.
再把a=1±代入到(*)式中.即得
y=(2+2)x-(2+2)或y=(2-2)x-(2-2).这就是所求的切线方程.
达标检测
1.答案:C
解析:根据导数的几何意义及切线的定义知曲线在(x0,y0)处有导数,则切线一定存在,但反之不一定成立,故A,B,D错误.
2.答案:C
解析:由题意可得: = =f ′(1),
即: =×2=1.故应选C.
3.答案:A
解析:因为f ′(1)= = = (2a+aΔx)=2a,
所以2a=2,所以a=1.
4.答案:x+2y+4=0
解析:f ′(-2)=
= = =-,
∴切线方程为y+1=-(x+2),即x+2y+4=0.
5.解:设切点P(m,n),切线斜率为k,
由y′= =
= (4x+2Δx)=4x,
得k=y′|x=m=4m.
由题意可知4m=8,∴m=2.
代入y=2x2-7得n=1.
故所求切点P为(2,1).
【学习目标】
1. 经历由平均变化率到瞬时变化率的过程,体会导数的概念的实际背景.
2. 了解导函数的概念,理解导数的几何意义.
3.根据导数的几何意义,会求曲线上某点处的切线方程.
4.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.
【学习过程】
一、课前预习
预习课本P64~69,思考并完成以下问题
(1)导数的几何意义是什么?
(2)导函数的概念是什么?怎样求导函数?
(3)怎么求过一点的曲线的切线方程?
二、课前小测
1.判断正误(正确的打“√”,错误的打“×”)
(1)函数y=f (x)在x=x0处的导数即为在该点处的斜率,也就是k=f ′(x0). ( )
(2)f ′(x1)>f ′(x2)反映了曲线在x=x1处比在x=x2处瞬时变化率较大. ( )
(3)f ′(x0)就是导函数y=f ′(x)在x0处的函数值. ( )
(4)若f ′(x0)=0,则曲线在x=x0处切线不存在. ( )
2.若曲线y=f (x)在点(x0,f (x0))处的切线方程为2x+y+1=0,则( )
A.f ′(x0)>0 B.f ′(x0)=0
C.f ′(x0)<0 D.f ′(x0)不存在
3.(教材P70习题T6改编)函数y=f (x)的图象如图所示,下列描述错误的是( )
A.x=-5处比x=-2处变化快
B.x=-4处呈上升趋势
C.x=1和x=2处增减趋势相反
D.x=0处呈上升趋势
4.已知函数f (x)在x0处的导数为f ′(x0)=1,则函数f (x)在x0处切线的倾斜角为________.
5.若函数f (x)在点A(1,2)处的导数是-1,那么过点A的切线方程是________.
三、新知探究
1.导数的概念
如果当Δx→0时,平均变化率无限趋近于一个确定的值,即有极限,则称y=f (x)在x=x0处可导,并把这个确定的值叫做y=f (x)在x=x0处的导数(也称为瞬时变化率),记作f ′(x0)或,即f ′(x0)= = .
思考:f ′(x0)>0和f ′(x0)<0反映了怎样的意义?
[提示] f ′(x0)>0反映了瞬时变化率呈增长趋势,
f ′(x0)<0反映了瞬时变化率呈下降趋势.
2.导数的几何意义
(1)导数的几何意义
如图,割线P0P的斜率k=. 记Δx=x-x0,当点P沿着曲线y=f (x)无限趋近于点P0时,即当Δx→0时,k无限趋近于函数y=f (x)在x=x0处的导数,因此,函数y=f(x)在x=x0处的导数f ′(x0)就是切线P0T的斜率k0,即k0==f ′(x0).
(2)切线方程
曲线y=f (x)在点(x0,f (x0))处的切线方程为y-f (x0)=f ′(x0)(x-x0).
3.导函数
对于函数y=f (x),当x=x0时,f ′(x0)是一个唯一确定的数,当x变化时,f ′(x)便是x的一个函数,我们称它为y=f (x)的导函数(简称为导数),即f ′(x)=y′= .
思考: f ′(x0)与f ′(x)有什么区别?
[提示] f ′(x0)是一个确定的数,而f ′(x)是一个函数.
四、题型突破
题型一 求函数在某点处的导数
【例1】 (1)若函数y=f (x)在x=x0处可导,则等于( )
A.f ′(x0) B.2f ′(x0) C.-2f ′(x0) D.0
(2)求函数y=3x2在x=1处的导数.
【反思感悟】
利用导数定义求导数
1 取极限前,要注意化简,保证使Δx→0时分母不为0.
2 函数在x0处的导数f ′ x0 只与x0有关,与Δx无关.
3 导数可以描述事物的瞬时变化率,应用非常广泛.
【跟踪训练】
1.建造一栋面积为x m2的房屋需要成本y万元,y是x的函数,y=f (x)=++0.3,求f ′(100),并解释它的实际意义.
题型二 导数几何意义的应用
【例2】 (1)已知函数y=f (x)的图象如图所示,则其导函数y=f ′(x)的图象可能是( )
A B C D
(2)某家电制造集团为尽快实现家电下乡提出四种运输方案,据预测,这四种方案均能在规定时间T内完成预期的运输任务Q0,各种方案的运输总量Q与时间t的函数关系如下所示.在这四种方案中,运输效率(单位时间内的运输量)逐步提高的是( )
A B C D
[思路探究] (1)切线斜率大于零,则f ′(x)>0;切线斜率小于零,则f ′(x)<0;
(2)要明确运输效率的含义,题设中已经给出运输效率即单位时间内的运输量,因此,运输效率逐步提高就是指Q′(t)不断增大.
【反思感悟】
导数几何意义理解中的两个关键
关键点一:y=f x 在点x=x0处的切线斜率为k,则k>0 f ′ x0 >0;k<0 f ′ x0 <0;k=0 f ′ x0 =0.
关键点二:|f ′ x0 |越大 在x0处瞬时变化越快;|f ′ x0 |越小 在x0处瞬时变化越慢.
【跟踪训练】
2.(1)已知y=f (x)的图象如图所示,则f ′(xA)与f ′(xB)的大小关系是( )
A.f ′(xA)>f ′(xB) B.f ′(xA)<f ′(xB)
C.f ′(xA)=f ′(xB) D.不能确定
(2)若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则( )
A.a=1,b=1 B.a=-1,b=1
C.a=1,b=-1 D.a=-1,b=-1
题型三 求切线方程
[探究问题]
1.如何求曲线f (x)在点(x0,f (x0))处的切线方程?
[提示] y-y0=k(x-x0).即根据导数的几何意义,求出函数y=f (x)在点(x0,f (x0))处的导数,即曲线在该点处的切线的斜率,再由直线方程的点斜式求出切线方程.
2.曲线f (x)在点(x0,f (x0))处的切线与曲线过点(x0,y0)的切线有什么不同?
[提示] 曲线f (x)在点(x0,f (x0))处的切线,点(x0,f (x0))一定是切点,只要求出k=f ′(x0),利用点斜式写出切线方程即可;而曲线f (x)过某点(x0,y0)的切线,给出的点(x0,y0)不一定在曲线上,即使在曲线上也不一定是切点.
3.曲线在某点处的切线是否与曲线只有一个交点?
[提示] 不一定.曲线y=f (x)在点P(x0,y0)处的切线l与曲线y=f (x)的交点个数不一定只有一个,如图所示.
【例3】 已知曲线C:y=x3.
(1)求曲线C在横坐标为x=1的点处的切线方程;
(2)求曲线C过点(1,1)的切线方程.
【多维探究】
1.把题中条件“y=x3”改成“y=x2”,求曲线在x=1点处的切线方程
2.求曲线y=x2+1过点P(1,0)的切线方程.
【反思感悟】
利用导数的几何意义求切线方程的方法
(1)若已知点(x0,y0)在已知曲线上,求在点(x0,y0)处的切线方程,先求出函数y=f (x)在点x0处的导数,然后根据直线的点斜式方程,得切线方程y-y0=f ′(x0)(x-x0).
(2)若点(x0,y0)不在曲线上,求过点(x0,y0)的切线方程,首先应设出切点坐标,然后根据导数的几何意义列出等式,求出切点坐标,进而求出切线方程.
五、达标检测
1.下面说法正确的是( )
A.若f ′(x0)不存在,则曲线y=f (x)在点(x0,f (x0))处没有切线
B.若曲线y=f (x)在点(x0,f (x0))处有切线,则f ′(x0)必存在
C.若f ′(x0)不存在,则曲线y=f (x)在点(x0,f (x0))处的切线斜率不存在
D.若曲线y=f (x)在点(x0,f (x0))处没有切线,则f ′(x0)有可能存在
2.已知函数y=f (x)是可导函数,且f ′(1)=2,则 =( )
A. B.2 C.1 D.-1
3.设曲线f (x)=ax2在点(1,a)处的切线与直线2x-y-6=0平行,则a等于( )
A.1 B. C.- D.-1
4.曲线f (x)=在点(-2,-1)处的切线方程为________.
5.已知曲线y=2x2-7在点P处的切线方程为8x-y-15=0,求切点P的坐标.
六、本课小结
1.函数f (x)在x=x0处的导数f ′(x0)=0并不能说明函数图象的上升与下降发生了转变,若函数在x=x0左右的导数都大于0,或者都小于0,则函数图象的走势并没有发生转变.如函数f (x)=x3在x=0处的导数等于0,但f (x)=x3的图象一直上升.
2.求切线方程时,不仅要检验已知点是否在曲线上,还要注意对“在”和“过”的理解.
(1)若“在”,则该点为切点.
(2)若“过”,则该点不一定是切点;若“过”曲线外的一点,则该点一定不是切点.
3.曲线在某点处切线斜率的大小反映了曲线在相应点处的变化情况,由切线的倾斜程度,可以判断出曲线升降的快慢.
参考答案
课前小测
1.答案:(1)√ (2)× (3)√ (4)×
提示:(1)根据导数的几何意义知正确.
(2)若|f (x0)|越大,瞬时变化率越大,故错误.
(3)根据导函数的定义知正确.
(4)若f ′(x0)=0说明曲线在x=x0处切线平行于x轴,不能说不存在.
2.答案:C
解析:由题意可知,f ′(x0)=-2<0,故选C.
3.答案:D
解析:根据导数的几何意义:f ′(-5)>0,f ′(-4)>0,f ′(-2)=0,f ′(0)<0,f ′(1)f ′(2)<0,故D错误,故选D.
4.答案:45°
设切线的倾斜角为α,则
tan α=f ′(x0) =1,又α∈[0°,180°),
∴α=45°.
5.答案:x+y-3=0
解析:切线的斜率为k=-1.
∴点 A(1,2)处的切线方程为y-2=-(x-1),
即x+y-3=0.
题型突破
【例1】(1)答案:B
解析:∵Δx=(x0+h)-(x0-h)=2h.
∴=2=2f ′(x0).故选B.
(2)解:∵Δy=f (1+Δx)-f (1)=3(1+Δx)2-3=6Δx+3(Δx)2,∴=6+3Δx,
∴f ′(1)= = (6+3Δx)=6.
【跟踪训练】
1.解:根据导数的定义,得f ′(100)= =
=
=
=
=+
=0.105.
f ′(100)=0.105表示当建筑面积为100 m2时,成本增加的速度为1 050元/m2.
【例2】答案:(1)B (2)B
解析:(1)由y=f (x)的图象及导数的几何意义可知,当x<0时,f ′(x)>0;当x=0时,f ′(x)=0;当x>0时,f ′(x)<0,故B符合.
(2)从函数图象上看,要求图象在[0,T]上越来越陡峭,在各选项中,只有B项中图象的切线斜率在不断增大,即运输效率(单位时间内的运输量)逐步提高.故选B.
【跟踪训练】
2.答案:(1)B (2)A
解析:(1)由导数的几何意义,f ′(xA),f ′(xB)分别是切线在点A、B处切线的斜率,由图象可知f ′(xA)<f ′(xB).
(2)由题意,知k=y′|x=0
= =1,∴a=1.
又点(0,b)在切线上,∴b=1,故选A.
【例3】解:(1)将x=1代入曲线C的方程得y=1,∴切点P(1,1).
y′|x=1= =
= [3+3Δx+(Δx)2]=3.
∴k=y′|x=1=3.
∴曲线在点P(1,1)处的切线方程为y-1=3(x-1),即3x-y-2=0.
(2)设切点为Q(x0,y0),由(1)可知=3x,由题意可知kPQ=,
即=3x,又y0=x,所以=3x,即2x-3x+1=0,解得x0=1或x0=-.
①当x0=1时,切点坐标为(1,1),相应的切线方程为3x-y-2=0.
②当x0=-时,切点坐标为,相应的切线方程为y+=,即3x-4y+1=0.
【多维探究】
1.解:把x=1代入y=x2得y=12=1.即切点P(1,1),
y′|x=1= =
= (Δx+2)=2,
∴k=y′|x=1=2.
∴曲线y=x2在P(1,1)处的切线方程为y-1=2(x-1),即2x-y-1=0.
2.解:设切点为Q,
k= = (2a+Δx)=2a.
∴在Q点处的切线方程为y-(a2+1)=2a(x-a). (*)
把点(1,0)代入(*)式得-(a2+1)=2a(1-a).
解的a=1±.
再把a=1±代入到(*)式中.即得
y=(2+2)x-(2+2)或y=(2-2)x-(2-2).这就是所求的切线方程.
达标检测
1.答案:C
解析:根据导数的几何意义及切线的定义知曲线在(x0,y0)处有导数,则切线一定存在,但反之不一定成立,故A,B,D错误.
2.答案:C
解析:由题意可得: = =f ′(1),
即: =×2=1.故应选C.
3.答案:A
解析:因为f ′(1)= = = (2a+aΔx)=2a,
所以2a=2,所以a=1.
4.答案:x+2y+4=0
解析:f ′(-2)=
= = =-,
∴切线方程为y+1=-(x+2),即x+2y+4=0.
5.解:设切点P(m,n),切线斜率为k,
由y′= =
= (4x+2Δx)=4x,
得k=y′|x=m=4m.
由题意可知4m=8,∴m=2.
代入y=2x2-7得n=1.
故所求切点P为(2,1).
