人教A版(2019)数学选择性必修二册期中复习:导数与函数的极值、最值导学案
文档属性
| 名称 | 人教A版(2019)数学选择性必修二册期中复习:导数与函数的极值、最值导学案 |  | |
| 格式 | docx | ||
| 文件大小 | 125.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 15:14:30 | ||
图片预览




文档简介
导数与函数的极值、最值
一、考纲分析
课程标准解读 关联考点 核心素养
借助函数的图象,了解函数在某点取得极值的必要条件和充分条件; 能利用导数求某些函数的极大值、极小值以及在给定闭区间上不超过三次的多项式函数的最大值、最小值; 会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次). 导数与函数的极值、最值. 1.逻辑推理. 2.直观想象. 3.数学运算.
二、本节重难点
求闭区间上函数的最大值、最小值
三、课前自测
1. 判断正误(正确的打“√”,错误的打“×”)
(1)函数在某区间上或定义域内的极大值是唯一的.( )
(2)导数为零的点不一定是极值点.( )
(3)函数的极大值不一定比极小值大.( )
(4)函数的极大值一定是函数的最大值.( )
(5)开区间上的单调连续函数无最值.( )
2.函数f(x)=(x2-1)2+2的极值点是( )
A.x=1 B.x=-1
C.x=1或-1或0 D.x=0
3.(多选)函数y=f(x)的导函数f′(x)的图象如图所示,以下命题错误的是( )
A.-3是函数y=f(x)的极值点
B.-1是函数y=f(x)的最小值点
C.y=f(x)在区间(-3,1)上单调递增
D.y=f(x)在x=0处切线的斜率小于零
4.(易错点)函数g(x)=-x2的极值点是________,函数f(x)=(x-1)3的极值点________.(填“存在”或“不存在”)
5.函数f(x)=4x-ln x的最小值为________.
四、考点梳理
1.函数的极值与导数
条件 f′(x0)=0
x0附近的左侧f′(x)>0,右侧f′(x)<0 x0附近的左侧f′(x)<0,右侧f′(x)>0
图象
极值 f(x0)为极大值 f(x0)为极小值
极值点 x0为极大值点 x0为极小值点
[注意] (1)函数的极值点一定出现在区间的内部,区间的端点不能称为极值点.
(2)在函数的整个定义域内,极值不一定是唯一的,有可能有多个极大值或极小值.
(3)极大值与极小值之间无确定的大小关系.
2.函数的最值
(1)在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值.
(2)若函数f(x)在[a,b]上单调递增,则f(a)为函数的最小值,f(b)为函数的最大值;若函数f(x)在[a,b]上单调递减,则f(a)为函数的最大值,f(b)为函数的最小值.
常用结论
1.若函数f(x)的图象连续不断,则f(x)在[a,b]上一定有最值.
2.若函数f(x)在[a,b]上是单调函数,则f(x)一定在区间端点处取得最值.
3.若函数f(x)在区间(a,b)内只有一个极值点,则相应的极值点一定是函数的最值点.
常见误区
1.对于可导函数f(x),“f′(x0)=0”是“函数f(x)在x=x0处有极值”的必要不充分条件.
2.求最值时,应注意极值点与所给区间的关系,关系不确定时,需要分类讨论,不可直接认为极值就是最值.
3.极值只能在定义域内部取得,而最值却可以在区间的端点处取得,有极值的未必有最值,有最值的未必有极值.
五、典例剖析
考点一 函数的极值问题
角度一 由图象判断函数的极值
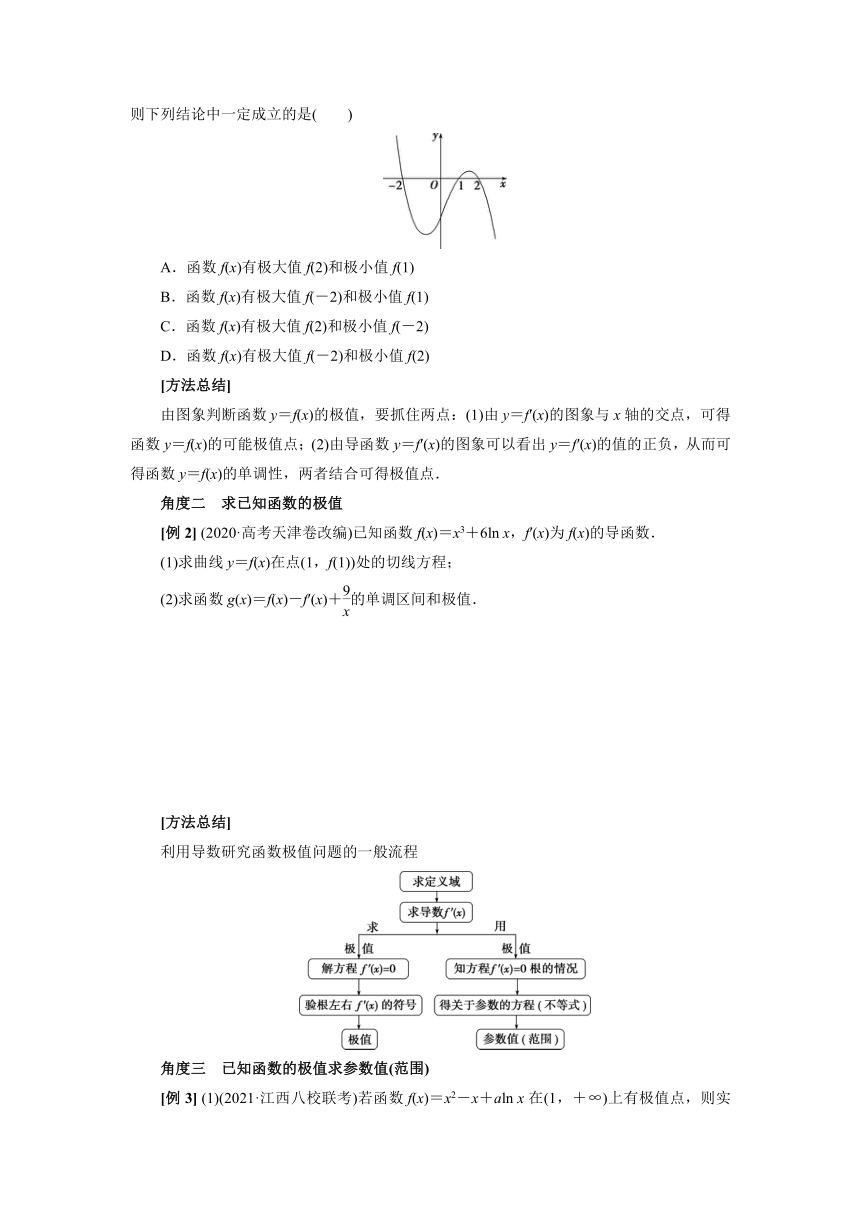
[例1] 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
[方法总结]
由图象判断函数y=f(x)的极值,要抓住两点:(1)由y=f′(x)的图象与x轴的交点,可得函数y=f(x)的可能极值点;(2)由导函数y=f′(x)的图象可以看出y=f′(x)的值的正负,从而可得函数y=f(x)的单调性,两者结合可得极值点.
角度二 求已知函数的极值
[例2] (2020·高考天津卷改编)已知函数f(x)=x3+6ln x,f′(x)为f(x)的导函数.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数g(x)=f(x)-f′(x)+的单调区间和极值.
[方法总结]
利用导数研究函数极值问题的一般流程
角度三 已知函数的极值求参数值(范围)
[例3] (1)(2021·江西八校联考)若函数f(x)=x2-x+aln x在(1,+∞)上有极值点,则实数a的取值范围为________.
(2)设函数f(x)=ln x+ax2-x,若x=1是函数f(x)的极大值点,则函数f(x)的极小值为________.
[方法总结]
已知函数极值点或极值求参数的两个要领
(1)列式:根据极值点处导数为0和极值这两个条件列方程组,利用待定系数法求解.
(2)验证:因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证根的合理性.
[注意] 若函数y=f(x)在区间(a,b)内有极值,那么y=f(x)在(a,b)内绝不是单调函数,即在某区间上单调函数没有极值.
[跟踪训练]
1.设函数f(x)=+ln x,则( )
A.x=为f(x)的极大值点
B.x=为f(x)的极小值点
C.x=2为f(x)的极大值点
D.x=2为f(x)的极小值点
2.已知f(x)=x3+3ax2+bx+a2在x=-1处有极值0,则a-b=________.
3.已知函数f(x)=ex(-x+ln x+a)(e为自然对数的底数,a为常数,且a≤1).判断函数f(x)在区间(1,e)内是否存在极值点,并说明理由.
考点二 函数的最值问题
[例4] (2020·高考北京卷节选)已知函数f(x)=12-x2.设曲线y=f(x)在点(t,f(t))处的切线与坐标轴围成的三角形的面积为S(t),求S(t)的最小值.
[方法总结]
求函数f(x)在[a,b]上最值的方法
(1)若函数在区间[a,b]上单调递增或递减,f(a)与f(b)一个为最大值,一个为最小值.
(2)若函数在闭区间[a,b]内有极值,要先求出[a,b]上的极值,与f(a),f(b)比较,最大的是最大值,最小的是最小值,可列表完成.
(3)函数f(x)在区间(a,b)上有唯一一个极值点,这个极值点就是最大(或最小)值点,此结论在导数的实际应用中经常用到.
[跟踪训练]
1.函数y=在[0,2]上的最大值是( )
A. B.
C.0 D.
2.已知函数f(x)=3ln x-x2+x在区间(1,3)上有最大值,则实数a的取值范围是( )
A. B.
C. D.
六、随堂训练
1.函数f(x)=3x2+ln x-2x的极值点的个数是( )
A.0 B.1
C.2 D.无数
2.f(x)=ex-x在区间[-1,1]上的最大值为________.
3.(2021·咸阳模拟)已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则=________.
4.函数f(x)=(x2-x-1)ex(其e=2.718…是自然对数的底数)的极值点是________;极大值为________.
5.设函数f(x)=x2+1-ln x.
(1)求f(x)的单调区间;
(2)求函数g(x)=f(x)-x在区间上的最小值.
七、本课小结
利用导数求函数的极值、最值是高考的热点,由函数的极值、最值求参数范围问题仍是高考的难点,题型各种类型都有,一般难度中等.
参考答案
课前自测
1.答案:(1)× (2)√ (3)√ (4)× (5)√
2.答案:C
解析:因为f(x)=x4-2x2+3,
所以由f′(x)=4x3-4x=4x(x+1)(x-1)=0得x=0或x=1或x=-1.
又当x<-1时,f′(x)<0,
当-10,
当01时,f′(x)>0,
所以x=0,1,-1都是函数f(x)的极值点.
3.答案:BD
解析:根据导函数的图象可知当x∈(-∞,-3)时,f′(x)<0,当x∈(-3,+∞)时,f′(x)≥0,
所以函数y=f(x)在(-∞,-3)上单调递减,在(-3,+∞)上单调递增,
则-3是函数y=f(x)的极值点,
因为函数y=f(x)在(-3,+∞)上单调递增,
所以-1不是函数y=f(x)的最小值点,
因为函数y=f(x)在x=0处的导数大于零,
所以y=f(x)在x=0处切线的斜率大于零,
故错误的命题为BD.
4.答案:0 不存在
解析:结合函数图象可知g(x)=-x2的极值点是x=0.因为f′(x)=3(x-1)2≥0,所以f′(x)=0无变号零点,故函数f(x)=(x-1)3不存在极值点.
5.答案:1+2ln 2
解析:函数f(x)的定义域为(0,+∞),由题意知f′(x)=4-=.
令f′(x)>0得x>,令f′(x)<0得0所以函数f(x)在上单调递减,在上单调递增,
所以当x=时,函数f(x)有最小值为f=4×-ln =1+ln 4=1+2ln 2.
典例剖析
[例1] 答案:D
解析:由题图可知,当x<-2时,f′(x)>0;当-22时,f′(x)>0.由此可以得到函数f(x)在x=-2处取得极大值,在x=2处取得极小值.故选D.
[例2]解:(1)因为f(x)=x3+6ln x,所以f′(x)=3x2+.
可得f(1)=1,f′(1)=9,
所以曲线y=f(x)在点(1,f(1))处的切线方程为y-1=9(x-1),即y=9x-8.
(2)依题意,g(x)=x3-3x2+6ln x+,x∈(0,+∞).
从而可得g′(x)=3x2-6x+-,整理可得g′(x)=.
令g′(x)=0,解得x=1.
当x变化时,g′(x),g(x)的变化情况如表所示:
x (0,1) 1 (1,+∞)
g′(x) - 0 +
g(x) ? 极小值 ?
所以函数g(x)的单调递减区间为(0,1),单调递增区间为(1,+∞);g(x)的极小值为g(1)=1,无极大值.
[例3] 答案:(1)(-∞,-1) (2)ln 2-2
解析:(1)函数f(x)的定义域为(0,+∞),
f′(x)=2x-1+=,
由题意知2x2-x+a=0在R上有两个不相等的实数解,且在(1,+∞)上有解,
所以Δ=1-8a>0,且2×12-1+a<0,
所以a∈(-∞,-1).
(2)函数f(x)=ln x+ax2-x,函数的定义域为(0,+∞),f′(x)=+2ax-.
若x=1是函数f(x)的极大值点,则f′(1)=0,解得a=;所以f(x)=ln x+x2-x,
f′(x)=+x-==;
当f′(x)>0时,02,
函数在(0,1)和(2,+∞)上单调递增;
当f′(x)<0时,1所以函数在x=1时有极大值,函数在x=2时有极小值为f(2)=ln 2-2.
[跟踪训练]
1.答案:D
解析:因为f(x)=+ln x(x>0),
所以f′(x)=-+,令f′(x)=0,则x=2.
当02时,f′(x)>0.
所以x=2为f(x)的极小值点.
2.答案:-7
解析:由题意得f′(x)=3x2+6ax+b,则
解得或
经检验当a=1,b=3时,函数f(x)在x=-1处无法取得极值,而a=2,b=9时满足题意,故a-b=-7.
3.解:不存在极值点.理由如下:
f′(x)=ex(ln x-x++a-1),
令g(x)=ln x-x++a-1,x∈(1,e),则f′(x)=exg(x),g′(x)=-<0恒成立,所以g(x)在(1,e)上单调递减,
所以g(x)所以函数f(x)在区间(1,e)内无极值点.
[例4] 解:因为f′(x)=-2x,则f′(t)=-2t,又f(t)=12-t2,
所以曲线y=f(x)在点(t,f(t))处的切线方程为y-(12-t2)=-2t(x-t),
即y=-2tx+t2+12.若t=0,则围不成三角形,故t≠0.
令x=0,得y=t2+12,记A(0,t2+12),O为坐标原点,
则|OA|=t2+12,令y=0,得x=,记B,
则|OB|=,
所以S(t)=|OA||OB|=,
因为S(t)为偶函数,所以仅考虑t>0即可.
当t>0时,S(t)=,
则S′(t)==(t2-4)(t2+12),
令S′(t)=0,得t=2,
所以当t变化时,S′(t)与S(t)的变化情况如表:
t (0,2) 2 (2,+∞)
S′(t) - 0 +
S(t) ? 极小值 ?
所以S(t)min=S(2)=32.
[跟踪训练]
1.答案:A
解析:易知y′=,x∈[0,2],令y′>0,得0≤x<1,令y′<0,得1所以函数y=在[0,1]上单调递增,在(1,2]上单调递减,
所以y=在[0,2]上的最大值是y|x=1=,故选A.
2.答案:B
解析:f′(x)=-2x+a-,
由题设知f′(x)=-2x+a-在(1,3)上只有一个零点且单调递减,
则问题转化为即 -随堂训练
1.答案:A
解析:函数定义域为(0,+∞),
且f′(x)=6x+-2=,令g(x)=6x2-2x+1,
由于x>0,g(x)=6x2-2x+1的Δ=-20<0,
所以g(x)>0恒成立,故f′(x)>0恒成立,
即f(x)在定义域上单调递增,无极值点.
2.答案:e-1
解析:f′(x)=ex-1,令f′(x)=0,得x=0,令f′(x)>0,得x>0,令f′(x)<0,得x<0,
则函数f(x)在(-1,0)上单调递减,在(0,1)上单调递增,
f(-1)=e-1+1,f(1)=e-1,f(-1)-f(1)=+2-e<+2-e<0,
所以f(1)>f(-1).所以最大值为e-1.
3.答案:1
解析:f′(x)=3ax2+2bx+c;
根据题图知,x=-1,2是f(x)的两个极值点,
所以x=-1,2是方程3ax2+2bx+c=0的两个实数根,
根据根与系数的关系得,
所以2b=-3a,c=-6a,
所以===1.
4.答案:1或-2
解析:由已知得f′(x)=(x2-x-1+2x-1)ex=(x2+x-2)ex=(x+2)(x-1)ex,
因为ex>0,令f′(x)=0,可得x=-2或x=1,
当x<-2时f′(x)>0,即函数f(x)在区间(-∞,-2)上单调递增;
当-2当x>1时,f′(x)>0,即函数f(x)在区间(1,+∞)上单调递增.
故f(x)的极值点为-2或1,且极大值为f(-2)=.
5.解:(1)易知f(x)的定义域为(0,+∞),f′(x)=2x-,
由f′(x)>0,得x>,由f′(x)<0,得0所以f(x)的单调递减区间为,单调递增区间为.
(2)由题意知g(x)=x2+1-ln x-x,g′(x)=2x--1=,由g′(x)>0,得x>1,由g′(x)≤0,得0所以g(x)在上单调递减,在(1,2)上单调递增,
所以在区间上,g(x)的最小值为g(1)=1.
一、考纲分析
课程标准解读 关联考点 核心素养
借助函数的图象,了解函数在某点取得极值的必要条件和充分条件; 能利用导数求某些函数的极大值、极小值以及在给定闭区间上不超过三次的多项式函数的最大值、最小值; 会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次). 导数与函数的极值、最值. 1.逻辑推理. 2.直观想象. 3.数学运算.
二、本节重难点
求闭区间上函数的最大值、最小值
三、课前自测
1. 判断正误(正确的打“√”,错误的打“×”)
(1)函数在某区间上或定义域内的极大值是唯一的.( )
(2)导数为零的点不一定是极值点.( )
(3)函数的极大值不一定比极小值大.( )
(4)函数的极大值一定是函数的最大值.( )
(5)开区间上的单调连续函数无最值.( )
2.函数f(x)=(x2-1)2+2的极值点是( )
A.x=1 B.x=-1
C.x=1或-1或0 D.x=0
3.(多选)函数y=f(x)的导函数f′(x)的图象如图所示,以下命题错误的是( )
A.-3是函数y=f(x)的极值点
B.-1是函数y=f(x)的最小值点
C.y=f(x)在区间(-3,1)上单调递增
D.y=f(x)在x=0处切线的斜率小于零
4.(易错点)函数g(x)=-x2的极值点是________,函数f(x)=(x-1)3的极值点________.(填“存在”或“不存在”)
5.函数f(x)=4x-ln x的最小值为________.
四、考点梳理
1.函数的极值与导数
条件 f′(x0)=0
x0附近的左侧f′(x)>0,右侧f′(x)<0 x0附近的左侧f′(x)<0,右侧f′(x)>0
图象
极值 f(x0)为极大值 f(x0)为极小值
极值点 x0为极大值点 x0为极小值点
[注意] (1)函数的极值点一定出现在区间的内部,区间的端点不能称为极值点.
(2)在函数的整个定义域内,极值不一定是唯一的,有可能有多个极大值或极小值.
(3)极大值与极小值之间无确定的大小关系.
2.函数的最值
(1)在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值.
(2)若函数f(x)在[a,b]上单调递增,则f(a)为函数的最小值,f(b)为函数的最大值;若函数f(x)在[a,b]上单调递减,则f(a)为函数的最大值,f(b)为函数的最小值.
常用结论
1.若函数f(x)的图象连续不断,则f(x)在[a,b]上一定有最值.
2.若函数f(x)在[a,b]上是单调函数,则f(x)一定在区间端点处取得最值.
3.若函数f(x)在区间(a,b)内只有一个极值点,则相应的极值点一定是函数的最值点.
常见误区
1.对于可导函数f(x),“f′(x0)=0”是“函数f(x)在x=x0处有极值”的必要不充分条件.
2.求最值时,应注意极值点与所给区间的关系,关系不确定时,需要分类讨论,不可直接认为极值就是最值.
3.极值只能在定义域内部取得,而最值却可以在区间的端点处取得,有极值的未必有最值,有最值的未必有极值.
五、典例剖析
考点一 函数的极值问题
角度一 由图象判断函数的极值
[例1] 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
[方法总结]
由图象判断函数y=f(x)的极值,要抓住两点:(1)由y=f′(x)的图象与x轴的交点,可得函数y=f(x)的可能极值点;(2)由导函数y=f′(x)的图象可以看出y=f′(x)的值的正负,从而可得函数y=f(x)的单调性,两者结合可得极值点.
角度二 求已知函数的极值
[例2] (2020·高考天津卷改编)已知函数f(x)=x3+6ln x,f′(x)为f(x)的导函数.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数g(x)=f(x)-f′(x)+的单调区间和极值.
[方法总结]
利用导数研究函数极值问题的一般流程
角度三 已知函数的极值求参数值(范围)
[例3] (1)(2021·江西八校联考)若函数f(x)=x2-x+aln x在(1,+∞)上有极值点,则实数a的取值范围为________.
(2)设函数f(x)=ln x+ax2-x,若x=1是函数f(x)的极大值点,则函数f(x)的极小值为________.
[方法总结]
已知函数极值点或极值求参数的两个要领
(1)列式:根据极值点处导数为0和极值这两个条件列方程组,利用待定系数法求解.
(2)验证:因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证根的合理性.
[注意] 若函数y=f(x)在区间(a,b)内有极值,那么y=f(x)在(a,b)内绝不是单调函数,即在某区间上单调函数没有极值.
[跟踪训练]
1.设函数f(x)=+ln x,则( )
A.x=为f(x)的极大值点
B.x=为f(x)的极小值点
C.x=2为f(x)的极大值点
D.x=2为f(x)的极小值点
2.已知f(x)=x3+3ax2+bx+a2在x=-1处有极值0,则a-b=________.
3.已知函数f(x)=ex(-x+ln x+a)(e为自然对数的底数,a为常数,且a≤1).判断函数f(x)在区间(1,e)内是否存在极值点,并说明理由.
考点二 函数的最值问题
[例4] (2020·高考北京卷节选)已知函数f(x)=12-x2.设曲线y=f(x)在点(t,f(t))处的切线与坐标轴围成的三角形的面积为S(t),求S(t)的最小值.
[方法总结]
求函数f(x)在[a,b]上最值的方法
(1)若函数在区间[a,b]上单调递增或递减,f(a)与f(b)一个为最大值,一个为最小值.
(2)若函数在闭区间[a,b]内有极值,要先求出[a,b]上的极值,与f(a),f(b)比较,最大的是最大值,最小的是最小值,可列表完成.
(3)函数f(x)在区间(a,b)上有唯一一个极值点,这个极值点就是最大(或最小)值点,此结论在导数的实际应用中经常用到.
[跟踪训练]
1.函数y=在[0,2]上的最大值是( )
A. B.
C.0 D.
2.已知函数f(x)=3ln x-x2+x在区间(1,3)上有最大值,则实数a的取值范围是( )
A. B.
C. D.
六、随堂训练
1.函数f(x)=3x2+ln x-2x的极值点的个数是( )
A.0 B.1
C.2 D.无数
2.f(x)=ex-x在区间[-1,1]上的最大值为________.
3.(2021·咸阳模拟)已知三次函数f(x)=ax3+bx2+cx+d的图象如图所示,则=________.
4.函数f(x)=(x2-x-1)ex(其e=2.718…是自然对数的底数)的极值点是________;极大值为________.
5.设函数f(x)=x2+1-ln x.
(1)求f(x)的单调区间;
(2)求函数g(x)=f(x)-x在区间上的最小值.
七、本课小结
利用导数求函数的极值、最值是高考的热点,由函数的极值、最值求参数范围问题仍是高考的难点,题型各种类型都有,一般难度中等.
参考答案
课前自测
1.答案:(1)× (2)√ (3)√ (4)× (5)√
2.答案:C
解析:因为f(x)=x4-2x2+3,
所以由f′(x)=4x3-4x=4x(x+1)(x-1)=0得x=0或x=1或x=-1.
又当x<-1时,f′(x)<0,
当-1
当0
所以x=0,1,-1都是函数f(x)的极值点.
3.答案:BD
解析:根据导函数的图象可知当x∈(-∞,-3)时,f′(x)<0,当x∈(-3,+∞)时,f′(x)≥0,
所以函数y=f(x)在(-∞,-3)上单调递减,在(-3,+∞)上单调递增,
则-3是函数y=f(x)的极值点,
因为函数y=f(x)在(-3,+∞)上单调递增,
所以-1不是函数y=f(x)的最小值点,
因为函数y=f(x)在x=0处的导数大于零,
所以y=f(x)在x=0处切线的斜率大于零,
故错误的命题为BD.
4.答案:0 不存在
解析:结合函数图象可知g(x)=-x2的极值点是x=0.因为f′(x)=3(x-1)2≥0,所以f′(x)=0无变号零点,故函数f(x)=(x-1)3不存在极值点.
5.答案:1+2ln 2
解析:函数f(x)的定义域为(0,+∞),由题意知f′(x)=4-=.
令f′(x)>0得x>,令f′(x)<0得0
所以当x=时,函数f(x)有最小值为f=4×-ln =1+ln 4=1+2ln 2.
典例剖析
[例1] 答案:D
解析:由题图可知,当x<-2时,f′(x)>0;当-2
[例2]解:(1)因为f(x)=x3+6ln x,所以f′(x)=3x2+.
可得f(1)=1,f′(1)=9,
所以曲线y=f(x)在点(1,f(1))处的切线方程为y-1=9(x-1),即y=9x-8.
(2)依题意,g(x)=x3-3x2+6ln x+,x∈(0,+∞).
从而可得g′(x)=3x2-6x+-,整理可得g′(x)=.
令g′(x)=0,解得x=1.
当x变化时,g′(x),g(x)的变化情况如表所示:
x (0,1) 1 (1,+∞)
g′(x) - 0 +
g(x) ? 极小值 ?
所以函数g(x)的单调递减区间为(0,1),单调递增区间为(1,+∞);g(x)的极小值为g(1)=1,无极大值.
[例3] 答案:(1)(-∞,-1) (2)ln 2-2
解析:(1)函数f(x)的定义域为(0,+∞),
f′(x)=2x-1+=,
由题意知2x2-x+a=0在R上有两个不相等的实数解,且在(1,+∞)上有解,
所以Δ=1-8a>0,且2×12-1+a<0,
所以a∈(-∞,-1).
(2)函数f(x)=ln x+ax2-x,函数的定义域为(0,+∞),f′(x)=+2ax-.
若x=1是函数f(x)的极大值点,则f′(1)=0,解得a=;所以f(x)=ln x+x2-x,
f′(x)=+x-==;
当f′(x)>0时,0
函数在(0,1)和(2,+∞)上单调递增;
当f′(x)<0时,1
[跟踪训练]
1.答案:D
解析:因为f(x)=+ln x(x>0),
所以f′(x)=-+,令f′(x)=0,则x=2.
当0
所以x=2为f(x)的极小值点.
2.答案:-7
解析:由题意得f′(x)=3x2+6ax+b,则
解得或
经检验当a=1,b=3时,函数f(x)在x=-1处无法取得极值,而a=2,b=9时满足题意,故a-b=-7.
3.解:不存在极值点.理由如下:
f′(x)=ex(ln x-x++a-1),
令g(x)=ln x-x++a-1,x∈(1,e),则f′(x)=exg(x),g′(x)=-<0恒成立,所以g(x)在(1,e)上单调递减,
所以g(x)
[例4] 解:因为f′(x)=-2x,则f′(t)=-2t,又f(t)=12-t2,
所以曲线y=f(x)在点(t,f(t))处的切线方程为y-(12-t2)=-2t(x-t),
即y=-2tx+t2+12.若t=0,则围不成三角形,故t≠0.
令x=0,得y=t2+12,记A(0,t2+12),O为坐标原点,
则|OA|=t2+12,令y=0,得x=,记B,
则|OB|=,
所以S(t)=|OA||OB|=,
因为S(t)为偶函数,所以仅考虑t>0即可.
当t>0时,S(t)=,
则S′(t)==(t2-4)(t2+12),
令S′(t)=0,得t=2,
所以当t变化时,S′(t)与S(t)的变化情况如表:
t (0,2) 2 (2,+∞)
S′(t) - 0 +
S(t) ? 极小值 ?
所以S(t)min=S(2)=32.
[跟踪训练]
1.答案:A
解析:易知y′=,x∈[0,2],令y′>0,得0≤x<1,令y′<0,得1
所以y=在[0,2]上的最大值是y|x=1=,故选A.
2.答案:B
解析:f′(x)=-2x+a-,
由题设知f′(x)=-2x+a-在(1,3)上只有一个零点且单调递减,
则问题转化为即 -
1.答案:A
解析:函数定义域为(0,+∞),
且f′(x)=6x+-2=,令g(x)=6x2-2x+1,
由于x>0,g(x)=6x2-2x+1的Δ=-20<0,
所以g(x)>0恒成立,故f′(x)>0恒成立,
即f(x)在定义域上单调递增,无极值点.
2.答案:e-1
解析:f′(x)=ex-1,令f′(x)=0,得x=0,令f′(x)>0,得x>0,令f′(x)<0,得x<0,
则函数f(x)在(-1,0)上单调递减,在(0,1)上单调递增,
f(-1)=e-1+1,f(1)=e-1,f(-1)-f(1)=+2-e<+2-e<0,
所以f(1)>f(-1).所以最大值为e-1.
3.答案:1
解析:f′(x)=3ax2+2bx+c;
根据题图知,x=-1,2是f(x)的两个极值点,
所以x=-1,2是方程3ax2+2bx+c=0的两个实数根,
根据根与系数的关系得,
所以2b=-3a,c=-6a,
所以===1.
4.答案:1或-2
解析:由已知得f′(x)=(x2-x-1+2x-1)ex=(x2+x-2)ex=(x+2)(x-1)ex,
因为ex>0,令f′(x)=0,可得x=-2或x=1,
当x<-2时f′(x)>0,即函数f(x)在区间(-∞,-2)上单调递增;
当-2
故f(x)的极值点为-2或1,且极大值为f(-2)=.
5.解:(1)易知f(x)的定义域为(0,+∞),f′(x)=2x-,
由f′(x)>0,得x>,由f′(x)<0,得0
(2)由题意知g(x)=x2+1-ln x-x,g′(x)=2x--1=,由g′(x)>0,得x>1,由g′(x)≤0,得0
所以在区间上,g(x)的最小值为g(1)=1.
