人教A版(2019)数学选择性必修第二册 5_1_1变化率问题课时精练(含答案)
文档属性
| 名称 | 人教A版(2019)数学选择性必修第二册 5_1_1变化率问题课时精练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 50.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 00:00:00 | ||
图片预览

文档简介
5.1.1变化率问题
一、常考题型
1.函数f (x)=x2-1在区间[1,m]上的平均变化率为3,则实数m的值为( )
A.3 B.2 C.1 D.4
2.已知一直线运动的物体,当时间从t变到t+Δt时物体的位移为Δs,那么 为( )
A.时间从t变到t+Δt时物体的速度
B.在t时刻该物体的瞬时速度
C.当时间为Δt时物体的速度
D.时间从t变到t+Δt时物体的平均速度
3.若函数f (x)在x0处有定义,则 的结果( )
A.与x0,h均无关
B.仅与x0有关,而与h无关
C.仅与h有关,而与x0无关
D.与x0,h均有关
4.在x=1附近,取Δx=0.3,在四个函数①y=x;②y=x2;③y=x3;④y=中,平均变化率最大的是( )
A.④ B.③
C.② D.①
5.枪弹在枪筒中运动可以看作匀加速运动,如果它的加速度是5.0×105 m/s2,枪弹从枪口射出时所用时间为1.6×10-3 s,则枪弹射出枪口时的瞬时速度为( )
A.800 m/s B.600 m/s
C.200 m/s D.400 m/s
6.已知汽车行驶的路程s和时间t之间的函数图象如图所示,在时间段[t0,t1],[t1,t2],[t2,t3]上的平均速度分别为,,,则三者的大小关系为________.(由大到小排列)
7.一物体位移s和时间t的关系是s=2t-3t2,则物体的初速度是__________.
8.若一物体的运动时间t(单位:s)与位移s(单位:m)的函数关系式为s=求此物体在t=1和t=5时的瞬时速度.
二、易错专项
9.已知函数f (x)在x0处的导数为1,则 等于( )
A.2 B.-2
C.1 D.-1
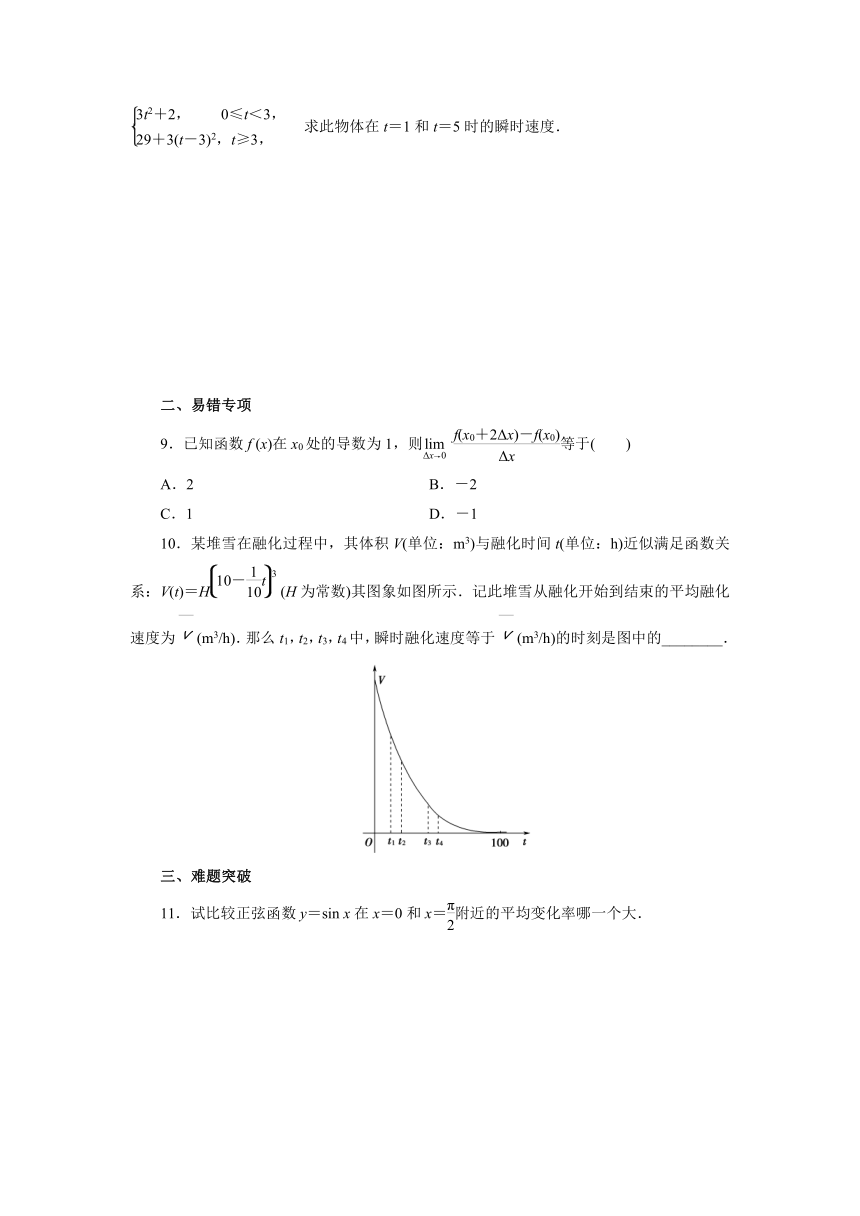
10.某堆雪在融化过程中,其体积V(单位:m3)与融化时间t(单位:h)近似满足函数关系:V(t)=H (H为常数)其图象如图所示.记此堆雪从融化开始到结束的平均融化速度为(m3/h).那么t1,t2,t3,t4中,瞬时融化速度等于(m3/h)的时刻是图中的________.
三、难题突破
11.试比较正弦函数y=sin x在x=0和x=附近的平均变化率哪一个大.
参考答案
1.B
解析:由已知得:=3,
∵m-1≠0,
∴m+1=3,∴m=2.
2.B
解析:表示从时间t到t+Δt时物体的平均速度,从而 表示在t时刻该物体的瞬时速度.选B.
3.B
解析:根据曲线在某点处切线斜率的意义知,该极限值只与x0有关,而与h没有关系.
4.B
解析:Δx=0.3时,①y=x在x=1附近的平均变化率k1=1;②y=x2在x=1附近的平均变化率k2=2+Δx=2.3;③y=x3在x=1附近的平均变化率k3=3+3Δx+(Δx)2=3.99;④y=在x=1附近的平均变化率k4=-=-.∴k3>k2>k1>k4,故应选B.
5.A
解析:位移公式为s=at2,∵Δs=a(t0+Δt)2-at=at0Δt+a(Δt)2,
∴=at0+aΔt,
∴ = =at0,
已知a=5.0×105 m/s2,t0=1.6×10-3 s,∴at0=800 m/s.所以枪弹射出枪口时的瞬时速度为800 m/s.
6.>>
解析:∵==kOA,==kAB,
==kBC.又∵由图象得kOA<kAB<kBC
∴>>.
7.2
解析:物体的速度为v=s′(t),
∴s′(t)=
=
= =2-6t.
即v=2-6t,
所以物体的初速度是v0=2-6×0=2.]
8.解:当t=1时,s=3t2+2,
∴v= = = (6+3Δt)=6.
当t=5时,s=29+3(t-3)2,
∴v= = (3Δt+12)=12.
故此物体在t=1和t=5时的瞬时速度分别是6 m/s和12 m/s.
9.A
解析: =2 =2f ′(x0)=2×1=2,故选A.
10.t3
解析:=,反映的是V(t)图象与坐标轴交点连线的斜率,观察可知t3处瞬时速度(即切线的斜率)与平均速度一致.
11.解:当自变量从0变到Δx时,函数的平均变化率为k1==.
当自变量从变到Δx+时,函数的平均变化率为k2==.
由于是在x=0和x=附近的平均变化率,故可知Δx较小,但Δx即可为正,又可为负.
当Δx>0时,k1>0,k2<0,即k1>k2;
当Δx<0时,k1-k2=-==.
∵Δx<0,∴Δx-<-,
∴sin<-,
从而有sin<-1,
sin+1<0,∴k1-k2>0,即k1>k2.
综上可知,正弦函数y=sin x在x=0附近的平均变化率大于在x=附近的平均变化率.
一、常考题型
1.函数f (x)=x2-1在区间[1,m]上的平均变化率为3,则实数m的值为( )
A.3 B.2 C.1 D.4
2.已知一直线运动的物体,当时间从t变到t+Δt时物体的位移为Δs,那么 为( )
A.时间从t变到t+Δt时物体的速度
B.在t时刻该物体的瞬时速度
C.当时间为Δt时物体的速度
D.时间从t变到t+Δt时物体的平均速度
3.若函数f (x)在x0处有定义,则 的结果( )
A.与x0,h均无关
B.仅与x0有关,而与h无关
C.仅与h有关,而与x0无关
D.与x0,h均有关
4.在x=1附近,取Δx=0.3,在四个函数①y=x;②y=x2;③y=x3;④y=中,平均变化率最大的是( )
A.④ B.③
C.② D.①
5.枪弹在枪筒中运动可以看作匀加速运动,如果它的加速度是5.0×105 m/s2,枪弹从枪口射出时所用时间为1.6×10-3 s,则枪弹射出枪口时的瞬时速度为( )
A.800 m/s B.600 m/s
C.200 m/s D.400 m/s
6.已知汽车行驶的路程s和时间t之间的函数图象如图所示,在时间段[t0,t1],[t1,t2],[t2,t3]上的平均速度分别为,,,则三者的大小关系为________.(由大到小排列)
7.一物体位移s和时间t的关系是s=2t-3t2,则物体的初速度是__________.
8.若一物体的运动时间t(单位:s)与位移s(单位:m)的函数关系式为s=求此物体在t=1和t=5时的瞬时速度.
二、易错专项
9.已知函数f (x)在x0处的导数为1,则 等于( )
A.2 B.-2
C.1 D.-1
10.某堆雪在融化过程中,其体积V(单位:m3)与融化时间t(单位:h)近似满足函数关系:V(t)=H (H为常数)其图象如图所示.记此堆雪从融化开始到结束的平均融化速度为(m3/h).那么t1,t2,t3,t4中,瞬时融化速度等于(m3/h)的时刻是图中的________.
三、难题突破
11.试比较正弦函数y=sin x在x=0和x=附近的平均变化率哪一个大.
参考答案
1.B
解析:由已知得:=3,
∵m-1≠0,
∴m+1=3,∴m=2.
2.B
解析:表示从时间t到t+Δt时物体的平均速度,从而 表示在t时刻该物体的瞬时速度.选B.
3.B
解析:根据曲线在某点处切线斜率的意义知,该极限值只与x0有关,而与h没有关系.
4.B
解析:Δx=0.3时,①y=x在x=1附近的平均变化率k1=1;②y=x2在x=1附近的平均变化率k2=2+Δx=2.3;③y=x3在x=1附近的平均变化率k3=3+3Δx+(Δx)2=3.99;④y=在x=1附近的平均变化率k4=-=-.∴k3>k2>k1>k4,故应选B.
5.A
解析:位移公式为s=at2,∵Δs=a(t0+Δt)2-at=at0Δt+a(Δt)2,
∴=at0+aΔt,
∴ = =at0,
已知a=5.0×105 m/s2,t0=1.6×10-3 s,∴at0=800 m/s.所以枪弹射出枪口时的瞬时速度为800 m/s.
6.>>
解析:∵==kOA,==kAB,
==kBC.又∵由图象得kOA<kAB<kBC
∴>>.
7.2
解析:物体的速度为v=s′(t),
∴s′(t)=
=
= =2-6t.
即v=2-6t,
所以物体的初速度是v0=2-6×0=2.]
8.解:当t=1时,s=3t2+2,
∴v= = = (6+3Δt)=6.
当t=5时,s=29+3(t-3)2,
∴v= = (3Δt+12)=12.
故此物体在t=1和t=5时的瞬时速度分别是6 m/s和12 m/s.
9.A
解析: =2 =2f ′(x0)=2×1=2,故选A.
10.t3
解析:=,反映的是V(t)图象与坐标轴交点连线的斜率,观察可知t3处瞬时速度(即切线的斜率)与平均速度一致.
11.解:当自变量从0变到Δx时,函数的平均变化率为k1==.
当自变量从变到Δx+时,函数的平均变化率为k2==.
由于是在x=0和x=附近的平均变化率,故可知Δx较小,但Δx即可为正,又可为负.
当Δx>0时,k1>0,k2<0,即k1>k2;
当Δx<0时,k1-k2=-==.
∵Δx<0,∴Δx-<-,
∴sin<-,
从而有sin<-1,
sin+1<0,∴k1-k2>0,即k1>k2.
综上可知,正弦函数y=sin x在x=0附近的平均变化率大于在x=附近的平均变化率.
