人教A版(2019)高中数学选择性必修第二册 第五章《一元函数的导数及其应用》知识归纳 课件(共55张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 第五章《一元函数的导数及其应用》知识归纳 课件(共55张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 17:08:26 | ||
图片预览











文档简介
(共55张PPT)
人教A版同步教材名师课件
导数及其应用
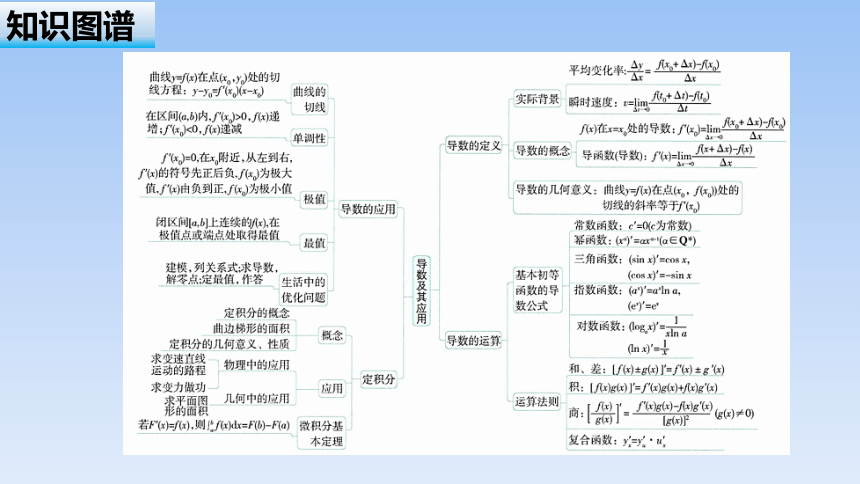
知识图谱
综合归纳
专题1 导数中的常见题型
一、曲线的切线
导数的几何意义是高考的常考内容,主要有以下几个命题角度:(1)求切线方程(斜率);(2)已知切线方程(或斜率)求切点、参数的值或曲线方程等.
利用导数的几何意义求切线方程的关键是搞清所给的点是不是切点,常见的类型有两种,一种是求“在某点处的切线方程”,则此点一定为切点,先求导,再求斜率,代入直线方程即可;另一种是求“过某点的切线方程”,这种类型中的点不一定是切点,可先设切点为Q(x1,y1),则切线方程为 ,再由切线过点 得
①
又 ②
由①②求出 的值,即可求出过点的切线方程.
例1(★★,2019安徽高三皖南八校联考)设函数设函数,若曲线在点 处的切线在轴上的截距为-2 ,在轴上的截距为2,求与的值.
思路分析 先求出 ,然后代入 ,求得 ,从而可确定切线方程,再根据切线的横纵截距求参数.
,
∴曲线在点 处的切线方程为,即 .
∵切线在轴上的截距为 .
又切线在轴上的截距为-2 ,
解析
主编点评
求参数的值,关键是构造关于的方程(组),解方程即可.
即时训练
1.(★★, 江苏淮安淮海中学高三阶测)若曲线在 处的切线与直线 垂直,则实数等于___________.
∵ ,
,即曲线在 处切线的斜率为 .
又∵该切线与直线垂直,∴ .
答案
解析
二、利用导数研究函数的单调性
1.利用导数求函数单调区间的步骤
(1)求函数 的定义域;
(2)求导数 ;
(3)在定义域内解不等式和,当不等式中带有参数时,要对参数进行分类讨论;
(4)确定函数 的单调区间.
2.已知函数单调性求参数的取值范围的方法
在已知单调性的情况下,一定要根据题意,仔细分析给定条件,选择最适合的方法求解.在实际解题过程中,常用的方法是根据单调性转化为不等式恒成立问题,进而利用参数分离法及最值法求解.
例2(★★,2018安徽滁州期末)已知函数在[-2,2]上的最大值为5,则实数的取值范围是( )
A. B. C. D.
思路分析 求导→判断单调性→分析最大值→解不等式→得 的范围.
当时, .
当时, ,当时, .
又 当
时,,要满足当 时, ,只需当 时, 即可.
解析
当时, ,
①当时, 2,符合题意;
②当时, ,因此 在[-1,0]上是增函数, <2,符合题意;
③当时, , 在 上是减函数,又 ,
∴令 解得 ,则 ,
综上,实数a的取值范围是[-ln2,+∞).
答案 D
即时训练
2.(★★)已知函数 .
(1)讨论 的单调性; (2)若≥0 ,求的取值范围.
(1)函数 的定义域为-2
①若 ,则,在 上单调递增.
②若 ,则由 得.
当 时,;
当 时, .
所以在 上单调递减,在 上单调递增.
解析
③若 ,则由得.
当时,;当 时, ,
故在 上单调递减,在 上单调递增.
(2)由(1)可知,当 时,函数 的最小值为,
因为≥0 ,所以 ,即 ;
当=0时,>0恒成立;
当<0时,函数 的最小值为 ,因为≥0 ,
所以 ,
解得 .
综上所述,的取值范围为[,1] .
三、利用导数求函数的极(最)值
1.求函数极值的步骤
(1)确定函数 的定义域;
(2)求导数;
(3)解方程=0 ,求出函数定义域内的所有根;
(4)列表检验 在 =0 的根 附近左右两侧值的符号,如果左正右负,那么在 处取极大值,如果左负右正,那么在 处取极小值.
2.求连续函数 在区间 上的最值的方法
(1)若函数 在区间 上单调递增或递减,则与 一个为最大值,一个为最小值;
(2)若函数在闭区间 内有极值,则要先求出 上的极值,再与,比较,最大的是最大值,最小的是最小值,可列表完成.
3.已知函数的极值(最值)情况求参数的值(取值范围)的方法
根据极值和最值的关系,与最值有关的问题一般可以转化为极值问题.
已知在某点 处有极值,求参数的值(取值范围)时,应逆向考虑,可先将参数当作常数,按照求极值的一般方法求解,再依据极值与导数的关系,列等式(不等式)求解.
例3(★★)已知函数在与 处都取得极值.
(1)求函数 的解析式及单调区间;
(2)求函数在区间 上的最大值与最小值.
思路分析(1)先求导,再根据题意得 解方程组即可求出 的值,进而写出函数的解析式,再利用导数求函数的单调区间.(2)比较函数的极值和端点函数值的大小即得函数在区间 上的最大值与最小值.
解析
(1)因为 ,所以,
由 得 解得
∴,
,令>0 ,得或 ,
令<0 ,得
函数的单调增区间是 ,单调减区间是 .
(2)由(1)可知,
-3 -2 2
+ 0 - 0 +
递增 极大 递减 极小 递增 11
从而极小值 ,极大值 ,而,
所以 .
主编点评 (1)本题主要考查利用导数研究函数的极值和最值,利用导数研究函数的单调区间,意在考查学生对这些知识的掌握水平和分析推理能力.
(2)求连续函数在闭区间上的最值,只要比较极值和端点函数值的大小.
即时训练
3.(★★,2019皖中名校联盟高三10月联考) 函数 .
(1)求曲线在点 处的切线方程;
(2)求函数在区间 上的最值.
解析
(1) + 1
在点处的切线方程为 .
(2)令 + 1(x∈ ),
恒 + + =2 ≥0成立,
∴函数 在 上单调递增,即 在 上单调递增,
∴当 时,单调递减,
当 时,,单调递增,
∴.
∵ = >0,
∴ ,∴= .
四、利用导数解决不等式恒成立及存在性问题
利用导数研究不等式恒成立和存在性问题,可先构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可先分离参数,构造函数,进而把问题转化为函数的最值问题.
例4(★★)已知.
(1)求 的单调区间;
(2)当2时,求证: 恒成立.
思路分析(1)求 的定义域和导数→令>0 ,解得 的增区间→
令<0 解得的减区间
(2)令=并求导→判断的单调性→证明 时的<0
(1) ,
当>0 时, ,解得 ;
当<0时, ,解得 ,
所以 的单调增区间为 ,单调减区间为 .
解析
(2)证明:当时,.
令 ,
则,
令 ,即 ,解得 或 (舍).
易知当 时,<0,在 上单调递减.
∴ ,即 .
即时训练
4.(★★)已知函数 .
(1)当 时, e]使不等式成立,求实数的取值范围;
(2)若在区间 上,函数 的图象恒在直线的下方,求实数的取值范围.
(1)当时, ,
可知当 e]时,为增函数,最小值为 .
因为 e]使不等式成立,所以 在e] 上的最小值小于或等于,故实数的取值范围是 .
解析
(2)在区间 上,函数的图象恒在直线的下方等价于对任意 ,即 在 上恒成立.
设,则 恒成立.
易知 ,
①当时, ,
为减函数,
∴ ,由题意知,
②当时,为增函数,
当时,,故此时不满足条件.
③当 时,在 上为减函数,在 上为增函数,
同样,当时, ,不满足题意.综上,实数的取值范围是 .
五、利用导数研究函数零点问题
利用导数研究函数零点问题,主要有两种方法
1.直接法:直接求导分析函数的单调性与极值、最值,画出函数的草图,利用根的个数判断函数图象与x轴的交点个数,从而确定最值的范围,进而求得参数的范围.
2.分离变量法:先将函数中的参数分离出来,将根的个数问题转化为直线y=a与新函数图象交点个数问题,从而转化为利用导数研究新构造的函数的单调性与极值问题(此时函数无参数,易于讨论).
例5(★★,福建莆田一中高三月考)已知函数 .
(1)当=e时,求 的单调区间;
(2)若有两个零点,求实数的取值范围.
思路分析(1)直接求导,导数大于0求得函数 的增区间,导数小于0求得函数 的减区间.(2)令 ,则=,再令= .在 上有两个零点等价于= 在 上有两个零点.通过讨论 的情况求出参数的取值范围.
(1) 的定义域为 ,当时, ,
,令>0 ,解得>1,令<0,解得 在 上为减函数;在 上为增函数.
解析
(2)令,则 在 上单调递增,且 ,
∴=,令=.
∴在 上有两个零点等价于= 在上有两个零点.
(1)当时, =在上递增,且>0 ,故 无零点;
(2)当 时, = 在上单调递增,
又,故 在上只有一个零点;
(3)当 时,由==0 ,
可知时,为减函数;
时, 为增函数,
∴在 时有唯一的一个极小值 .
若e,则无零点;
若e ,则0,只有一个零点;
若e ,则 ,而 ,
由于 在e 时为减函数,可知当e时, .
从而 >0 ,
∴在 和 上各有一个零点.
综上可知:当e 时,有两个零点,即所求的取值范围是 .
主播点评
本题主要考查函数的单调性,根据函数零点个数求参数的取值范围.本题的易错点是对实数分类不准确.换元是个特殊技巧:= = =.
即时训练
5.(★★2019皖南八校联考)已知函数 .
(1)求证:对任意 ,有 ;
(2)若 在实数集内有2个零点,求实数的取值范围.
(1)证明:∵ ,∴ .令0 ,解得0 .
当 变化时,的变化情况如下表:
解析
0
+ 0 -
极大值1
∴ 在 内是增函数,在 内是减函数.
∴时, .
, .若,则恒成立,
∴在内单调递增,不可能有2个零点.
若 ,则由0 ,得.
令 ,得 ;令 ,得 .
∴在 内单调递减,在 内单调递增,由题意,则 ,∴ ,∴ .
证明如下:时,有2个零点,
由 及单调性知 在 内有1个零点.
∵时, ,∴ ,
取 ,则 ,
+1 2( )2[]1.
由(1)知 ≥1>,取 ,
则> ,
由的单调性知 在
内有1个零点,∴有2个零点时, .
六、利用导数证明不等式
利用导数证明不等式的思路
1.我们知道函数在某个区间上的导数值大于(小于)0时,该函数在该区间上单调递增(减).因而在证明不等式时,根据不等式的特点,有时可以构造函数,用导数证明该函数的单调性,然后利用函数单调性达到证明不等式的目的,即把证明不等式转化为证明函数的单调性.
2.导数可用于求函数的最值,因而在证明不等式时,根据不等式的特点,有时可以构造函数,用导数求出该函数的最值,从而推出不等式恒成立,即把证明不等式问题转化为求函数的最值问题.
例6(★★)已知函数 .
(1)若在 上存在极值,求实数的取值范围;
(2)求证:当时, .
(1)由题知 ,令 0,得 ;令 0 ,得,∴在(0,1)上单调递增;在(1,+∞)上单调递减.
故是函数的极大值点,又 在 上存在极值,
∴,即 ,故实数的取值范围是 .
解析
(2)证明:要证 ,即证 ,
令 ,则,
再令 ,则 .
当时,在(1,+∞) 上是增函数,
∴在 (1,+∞)上是增函数,
∴当 时,> ,令= ,
则 =2 = .
∵当 时, <0,∴ <0,即 在(1,+∞) 上是减函数,
∴当时, < = ,∴ >,即 >.
主编点评
利用导数证明不等式常见的解题策略:(1)构造差函数 .根据差函数的导函数符号,确定差函数的单调性,利用单调性得不等量关系,进而证明不等式.(2)根据条件,寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放缩、等量代换将多元函数转化为一元函数.
即时训练
6.(★★,四川高三诊断性测试)已知函数 .
(1)求曲线 在点 处的切线方程;
(2)设 ,证明: .
(1)由题意易得 , ,所以 ,
因此 在点 处的切线方程为 ,即 .
(2)证明:因为 ,所以.
由于 ,
等价于 ,
解析
令 ,则.设函数 ,
,
当 时, ,所以 ,
所以在 上是增函数,又 ,所以,
所以 ,即 .①
等价于
令 ,则 .设函数
当 时, ,所以 ,所以在(1,+∞) 上是减函数,
又 ,所以 ,所以 ,
即 .②
综合①②可得: .
七、导数与生活中的优化问题
解决生活中的优化问题时,一般要注意以下几点:
(1)在求实际问题中的最大(小)值时,一定要考虑问题的实际意义,不符合实际意义的值应舍去.例如,长度、宽度应大于零,销售价格应为正数.
(2)在解决优化问题时,不仅要注意将问题中涉及的变量关系用函数关系表示,还应确定函数的定义域.
(3)得出函数的最大值或最小值之后,一定要将数学问题还原成实际问题.
例7(★★★)某旅游景点预计2019年1月份起前个月的旅游人数的和(单位:万人)与 的关系近似地满足 ,且 .已知第个月的人均消费额 (单位:元)与的近似关系是
(1)写出2019年第个月的旅游人数 (单位:万人)与的函数关系式;
(2)问2019年第几个月旅游消费总额最大 最大月旅游消费总额为多少元
解析
(1)当=1时,,当 ,且 时,
验证=1也满足此式,所以,且 .
(2)第个月旅游消费总额(单位:万元)为
即
(i)当 ,且时,
令0 ,解得 或 (舍去).
当 时,0 ,当 时,0 ,
∴当时,.
(ii)当 ,且 时,是减函数,
∴当时,.
综上,2019年5月份的旅游消费总额最大,最大旅游消费总额为3125万元.
即时训练
7.(★★★)某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产万件,需另投入流动成本 万元,当年产量小于7万件时,(万元);当年产量不小于7万件时, (万元).已知每件产品售价为6元,假如该同学生产的产品全部售完.
(1)写出年利润 (万元)关于年产量(万件)的函数解析式;
(注:年利润=年销售收入-固定成本-流动成本)
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大 最大年利润是多少 (取≈20 )
(1)每件产品售价为6元,则万件产品销售收入为 万元.
依题意得,当 时, .
当时,.
∴
解析
(2)当 时,,
∴当 时, 取最大值,最大值为=10 .
当时,, = ,
∴当 时,>0 ,函数 单调递增;
当 时,<0 ,函数 单调递减.
∴当时,取最大值,最大值为=15 ln 1=11 (万元).
∵11>10 ,
∴当≈20 时, 取得最大值11万元,
即当年产量约为20万件时,该同学的这一产品所获年利润最大,最大利润为11万元.
专题2 常考重要函数模型
1.型
求导: 令0,得函数有极值点 .
它的图象和性质如下:
符号
图象
定义域 单调性
最值
2.型
求导:令0 ,得函数有极值点,其中 .
当时,>0 ,函数在R 上单调递增.它的图象和性质如下:
图象
定义域 R 单调性 在R上单调递增 在 上单调递减,在 上单调递增
值域 R
过定点 (0,1) 3. ,型
求导:∵ ,令0 ,得 有极值点1.
= ,令0 ,得 有极值点1 .
,
令0 ,得有极值点1 .它们的图象和性质如下:
函数
图象
x→+∞时,图象无限靠近x轴 x→-∞时,图象无限靠近x轴,x→0(从右侧)时,图象无限靠近y轴正半轴,x→0(从左侧)时,图象无限靠近y轴负半轴 x→-∞时,图象无限靠近x轴
定义域 R {x|x≠0} R
单调性 在(-∞,1)上单调递增,在(1,+∞)上单调递减 在(-∞,0)和(0,1)上单调递减,在(1,+∞)上单调递增 在(-∞,-1)上单调递减,在
(-1,+∞)上单调递增
值域
4.
求导:.令0 ,得有极值点 .
.令0 ,得 有极值点e .
.令0 ,得有极值点e .
它们的图象和性质如下:
函数
图象
定义域
单调性 在(0,1),(1,e)上单调递减,在(e,+∞) 上单调递增
最值 在 (1,+∞)上有最小值e
人教A版同步教材名师课件
导数及其应用
知识图谱
综合归纳
专题1 导数中的常见题型
一、曲线的切线
导数的几何意义是高考的常考内容,主要有以下几个命题角度:(1)求切线方程(斜率);(2)已知切线方程(或斜率)求切点、参数的值或曲线方程等.
利用导数的几何意义求切线方程的关键是搞清所给的点是不是切点,常见的类型有两种,一种是求“在某点处的切线方程”,则此点一定为切点,先求导,再求斜率,代入直线方程即可;另一种是求“过某点的切线方程”,这种类型中的点不一定是切点,可先设切点为Q(x1,y1),则切线方程为 ,再由切线过点 得
①
又 ②
由①②求出 的值,即可求出过点的切线方程.
例1(★★,2019安徽高三皖南八校联考)设函数设函数,若曲线在点 处的切线在轴上的截距为-2 ,在轴上的截距为2,求与的值.
思路分析 先求出 ,然后代入 ,求得 ,从而可确定切线方程,再根据切线的横纵截距求参数.
,
∴曲线在点 处的切线方程为,即 .
∵切线在轴上的截距为 .
又切线在轴上的截距为-2 ,
解析
主编点评
求参数的值,关键是构造关于的方程(组),解方程即可.
即时训练
1.(★★, 江苏淮安淮海中学高三阶测)若曲线在 处的切线与直线 垂直,则实数等于___________.
∵ ,
,即曲线在 处切线的斜率为 .
又∵该切线与直线垂直,∴ .
答案
解析
二、利用导数研究函数的单调性
1.利用导数求函数单调区间的步骤
(1)求函数 的定义域;
(2)求导数 ;
(3)在定义域内解不等式和,当不等式中带有参数时,要对参数进行分类讨论;
(4)确定函数 的单调区间.
2.已知函数单调性求参数的取值范围的方法
在已知单调性的情况下,一定要根据题意,仔细分析给定条件,选择最适合的方法求解.在实际解题过程中,常用的方法是根据单调性转化为不等式恒成立问题,进而利用参数分离法及最值法求解.
例2(★★,2018安徽滁州期末)已知函数在[-2,2]上的最大值为5,则实数的取值范围是( )
A. B. C. D.
思路分析 求导→判断单调性→分析最大值→解不等式→得 的范围.
当时, .
当时, ,当时, .
又 当
时,,要满足当 时, ,只需当 时, 即可.
解析
当时, ,
①当时, 2,符合题意;
②当时, ,因此 在[-1,0]上是增函数, <2,符合题意;
③当时, , 在 上是减函数,又 ,
∴令 解得 ,则 ,
综上,实数a的取值范围是[-ln2,+∞).
答案 D
即时训练
2.(★★)已知函数 .
(1)讨论 的单调性; (2)若≥0 ,求的取值范围.
(1)函数 的定义域为-2
①若 ,则,在 上单调递增.
②若 ,则由 得.
当 时,;
当 时, .
所以在 上单调递减,在 上单调递增.
解析
③若 ,则由得.
当时,;当 时, ,
故在 上单调递减,在 上单调递增.
(2)由(1)可知,当 时,函数 的最小值为,
因为≥0 ,所以 ,即 ;
当=0时,>0恒成立;
当<0时,函数 的最小值为 ,因为≥0 ,
所以 ,
解得 .
综上所述,的取值范围为[,1] .
三、利用导数求函数的极(最)值
1.求函数极值的步骤
(1)确定函数 的定义域;
(2)求导数;
(3)解方程=0 ,求出函数定义域内的所有根;
(4)列表检验 在 =0 的根 附近左右两侧值的符号,如果左正右负,那么在 处取极大值,如果左负右正,那么在 处取极小值.
2.求连续函数 在区间 上的最值的方法
(1)若函数 在区间 上单调递增或递减,则与 一个为最大值,一个为最小值;
(2)若函数在闭区间 内有极值,则要先求出 上的极值,再与,比较,最大的是最大值,最小的是最小值,可列表完成.
3.已知函数的极值(最值)情况求参数的值(取值范围)的方法
根据极值和最值的关系,与最值有关的问题一般可以转化为极值问题.
已知在某点 处有极值,求参数的值(取值范围)时,应逆向考虑,可先将参数当作常数,按照求极值的一般方法求解,再依据极值与导数的关系,列等式(不等式)求解.
例3(★★)已知函数在与 处都取得极值.
(1)求函数 的解析式及单调区间;
(2)求函数在区间 上的最大值与最小值.
思路分析(1)先求导,再根据题意得 解方程组即可求出 的值,进而写出函数的解析式,再利用导数求函数的单调区间.(2)比较函数的极值和端点函数值的大小即得函数在区间 上的最大值与最小值.
解析
(1)因为 ,所以,
由 得 解得
∴,
,令>0 ,得或 ,
令<0 ,得
函数的单调增区间是 ,单调减区间是 .
(2)由(1)可知,
-3 -2 2
+ 0 - 0 +
递增 极大 递减 极小 递增 11
从而极小值 ,极大值 ,而,
所以 .
主编点评 (1)本题主要考查利用导数研究函数的极值和最值,利用导数研究函数的单调区间,意在考查学生对这些知识的掌握水平和分析推理能力.
(2)求连续函数在闭区间上的最值,只要比较极值和端点函数值的大小.
即时训练
3.(★★,2019皖中名校联盟高三10月联考) 函数 .
(1)求曲线在点 处的切线方程;
(2)求函数在区间 上的最值.
解析
(1) + 1
在点处的切线方程为 .
(2)令 + 1(x∈ ),
恒 + + =2 ≥0成立,
∴函数 在 上单调递增,即 在 上单调递增,
∴当 时,单调递减,
当 时,,单调递增,
∴.
∵ = >0,
∴ ,∴= .
四、利用导数解决不等式恒成立及存在性问题
利用导数研究不等式恒成立和存在性问题,可先构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可先分离参数,构造函数,进而把问题转化为函数的最值问题.
例4(★★)已知.
(1)求 的单调区间;
(2)当2时,求证: 恒成立.
思路分析(1)求 的定义域和导数→令>0 ,解得 的增区间→
令<0 解得的减区间
(2)令=并求导→判断的单调性→证明 时的<0
(1) ,
当>0 时, ,解得 ;
当<0时, ,解得 ,
所以 的单调增区间为 ,单调减区间为 .
解析
(2)证明:当时,.
令 ,
则,
令 ,即 ,解得 或 (舍).
易知当 时,<0,在 上单调递减.
∴ ,即 .
即时训练
4.(★★)已知函数 .
(1)当 时, e]使不等式成立,求实数的取值范围;
(2)若在区间 上,函数 的图象恒在直线的下方,求实数的取值范围.
(1)当时, ,
可知当 e]时,为增函数,最小值为 .
因为 e]使不等式成立,所以 在e] 上的最小值小于或等于,故实数的取值范围是 .
解析
(2)在区间 上,函数的图象恒在直线的下方等价于对任意 ,即 在 上恒成立.
设,则 恒成立.
易知 ,
①当时, ,
为减函数,
∴ ,由题意知,
②当时,为增函数,
当时,,故此时不满足条件.
③当 时,在 上为减函数,在 上为增函数,
同样,当时, ,不满足题意.综上,实数的取值范围是 .
五、利用导数研究函数零点问题
利用导数研究函数零点问题,主要有两种方法
1.直接法:直接求导分析函数的单调性与极值、最值,画出函数的草图,利用根的个数判断函数图象与x轴的交点个数,从而确定最值的范围,进而求得参数的范围.
2.分离变量法:先将函数中的参数分离出来,将根的个数问题转化为直线y=a与新函数图象交点个数问题,从而转化为利用导数研究新构造的函数的单调性与极值问题(此时函数无参数,易于讨论).
例5(★★,福建莆田一中高三月考)已知函数 .
(1)当=e时,求 的单调区间;
(2)若有两个零点,求实数的取值范围.
思路分析(1)直接求导,导数大于0求得函数 的增区间,导数小于0求得函数 的减区间.(2)令 ,则=,再令= .在 上有两个零点等价于= 在 上有两个零点.通过讨论 的情况求出参数的取值范围.
(1) 的定义域为 ,当时, ,
,令>0 ,解得>1,令<0,解得 在 上为减函数;在 上为增函数.
解析
(2)令,则 在 上单调递增,且 ,
∴=,令=.
∴在 上有两个零点等价于= 在上有两个零点.
(1)当时, =在上递增,且>0 ,故 无零点;
(2)当 时, = 在上单调递增,
又,故 在上只有一个零点;
(3)当 时,由==0 ,
可知时,为减函数;
时, 为增函数,
∴在 时有唯一的一个极小值 .
若e,则无零点;
若e ,则0,只有一个零点;
若e ,则 ,而 ,
由于 在e 时为减函数,可知当e时, .
从而 >0 ,
∴在 和 上各有一个零点.
综上可知:当e 时,有两个零点,即所求的取值范围是 .
主播点评
本题主要考查函数的单调性,根据函数零点个数求参数的取值范围.本题的易错点是对实数分类不准确.换元是个特殊技巧:= = =.
即时训练
5.(★★2019皖南八校联考)已知函数 .
(1)求证:对任意 ,有 ;
(2)若 在实数集内有2个零点,求实数的取值范围.
(1)证明:∵ ,∴ .令0 ,解得0 .
当 变化时,的变化情况如下表:
解析
0
+ 0 -
极大值1
∴ 在 内是增函数,在 内是减函数.
∴时, .
, .若,则恒成立,
∴在内单调递增,不可能有2个零点.
若 ,则由0 ,得.
令 ,得 ;令 ,得 .
∴在 内单调递减,在 内单调递增,由题意,则 ,∴ ,∴ .
证明如下:时,有2个零点,
由 及单调性知 在 内有1个零点.
∵时, ,∴ ,
取 ,则 ,
+1 2( )2[]1.
由(1)知 ≥1>,取 ,
则> ,
由的单调性知 在
内有1个零点,∴有2个零点时, .
六、利用导数证明不等式
利用导数证明不等式的思路
1.我们知道函数在某个区间上的导数值大于(小于)0时,该函数在该区间上单调递增(减).因而在证明不等式时,根据不等式的特点,有时可以构造函数,用导数证明该函数的单调性,然后利用函数单调性达到证明不等式的目的,即把证明不等式转化为证明函数的单调性.
2.导数可用于求函数的最值,因而在证明不等式时,根据不等式的特点,有时可以构造函数,用导数求出该函数的最值,从而推出不等式恒成立,即把证明不等式问题转化为求函数的最值问题.
例6(★★)已知函数 .
(1)若在 上存在极值,求实数的取值范围;
(2)求证:当时, .
(1)由题知 ,令 0,得 ;令 0 ,得,∴在(0,1)上单调递增;在(1,+∞)上单调递减.
故是函数的极大值点,又 在 上存在极值,
∴,即 ,故实数的取值范围是 .
解析
(2)证明:要证 ,即证 ,
令 ,则,
再令 ,则 .
当时,在(1,+∞) 上是增函数,
∴在 (1,+∞)上是增函数,
∴当 时,> ,令= ,
则 =2 = .
∵当 时, <0,∴ <0,即 在(1,+∞) 上是减函数,
∴当时, < = ,∴ >,即 >.
主编点评
利用导数证明不等式常见的解题策略:(1)构造差函数 .根据差函数的导函数符号,确定差函数的单调性,利用单调性得不等量关系,进而证明不等式.(2)根据条件,寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放缩、等量代换将多元函数转化为一元函数.
即时训练
6.(★★,四川高三诊断性测试)已知函数 .
(1)求曲线 在点 处的切线方程;
(2)设 ,证明: .
(1)由题意易得 , ,所以 ,
因此 在点 处的切线方程为 ,即 .
(2)证明:因为 ,所以.
由于 ,
等价于 ,
解析
令 ,则.设函数 ,
,
当 时, ,所以 ,
所以在 上是增函数,又 ,所以,
所以 ,即 .①
等价于
令 ,则 .设函数
当 时, ,所以 ,所以在(1,+∞) 上是减函数,
又 ,所以 ,所以 ,
即 .②
综合①②可得: .
七、导数与生活中的优化问题
解决生活中的优化问题时,一般要注意以下几点:
(1)在求实际问题中的最大(小)值时,一定要考虑问题的实际意义,不符合实际意义的值应舍去.例如,长度、宽度应大于零,销售价格应为正数.
(2)在解决优化问题时,不仅要注意将问题中涉及的变量关系用函数关系表示,还应确定函数的定义域.
(3)得出函数的最大值或最小值之后,一定要将数学问题还原成实际问题.
例7(★★★)某旅游景点预计2019年1月份起前个月的旅游人数的和(单位:万人)与 的关系近似地满足 ,且 .已知第个月的人均消费额 (单位:元)与的近似关系是
(1)写出2019年第个月的旅游人数 (单位:万人)与的函数关系式;
(2)问2019年第几个月旅游消费总额最大 最大月旅游消费总额为多少元
解析
(1)当=1时,,当 ,且 时,
验证=1也满足此式,所以,且 .
(2)第个月旅游消费总额(单位:万元)为
即
(i)当 ,且时,
令0 ,解得 或 (舍去).
当 时,0 ,当 时,0 ,
∴当时,.
(ii)当 ,且 时,是减函数,
∴当时,.
综上,2019年5月份的旅游消费总额最大,最大旅游消费总额为3125万元.
即时训练
7.(★★★)某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产万件,需另投入流动成本 万元,当年产量小于7万件时,(万元);当年产量不小于7万件时, (万元).已知每件产品售价为6元,假如该同学生产的产品全部售完.
(1)写出年利润 (万元)关于年产量(万件)的函数解析式;
(注:年利润=年销售收入-固定成本-流动成本)
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大 最大年利润是多少 (取≈20 )
(1)每件产品售价为6元,则万件产品销售收入为 万元.
依题意得,当 时, .
当时,.
∴
解析
(2)当 时,,
∴当 时, 取最大值,最大值为=10 .
当时,, = ,
∴当 时,>0 ,函数 单调递增;
当 时,<0 ,函数 单调递减.
∴当时,取最大值,最大值为=15 ln 1=11 (万元).
∵11>10 ,
∴当≈20 时, 取得最大值11万元,
即当年产量约为20万件时,该同学的这一产品所获年利润最大,最大利润为11万元.
专题2 常考重要函数模型
1.型
求导: 令0,得函数有极值点 .
它的图象和性质如下:
符号
图象
定义域 单调性
最值
2.型
求导:令0 ,得函数有极值点,其中 .
当时,>0 ,函数在R 上单调递增.它的图象和性质如下:
图象
定义域 R 单调性 在R上单调递增 在 上单调递减,在 上单调递增
值域 R
过定点 (0,1) 3. ,型
求导:∵ ,令0 ,得 有极值点1.
= ,令0 ,得 有极值点1 .
,
令0 ,得有极值点1 .它们的图象和性质如下:
函数
图象
x→+∞时,图象无限靠近x轴 x→-∞时,图象无限靠近x轴,x→0(从右侧)时,图象无限靠近y轴正半轴,x→0(从左侧)时,图象无限靠近y轴负半轴 x→-∞时,图象无限靠近x轴
定义域 R {x|x≠0} R
单调性 在(-∞,1)上单调递增,在(1,+∞)上单调递减 在(-∞,0)和(0,1)上单调递减,在(1,+∞)上单调递增 在(-∞,-1)上单调递减,在
(-1,+∞)上单调递增
值域
4.
求导:.令0 ,得有极值点 .
.令0 ,得 有极值点e .
.令0 ,得有极值点e .
它们的图象和性质如下:
函数
图象
定义域
单调性 在(0,1),(1,e)上单调递减,在(e,+∞) 上单调递增
最值 在 (1,+∞)上有最小值e
