人教A版(2019)高中数学选择性必修第三册 6.1_分类加法原理和分步乘法原理课件(共25张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 6.1_分类加法原理和分步乘法原理课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 544.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 20:10:27 | ||
图片预览








文档简介
(共25张PPT)
§6.1 分类加法计数原理与分布乘法计数原理(一)
1.理解分类加法计数原理与分类乘法计数原理.
2.会用这两个原理分析和解决一些简单的实际计数问题.
问题导学
题型探究
达标检测
学习目标
答案
问题导学 新知探究 点点落实
知识点一 分类加法计数原理
第十二届全运会在中国辽宁盛大召开,一名志愿者从济南赶赴沈阳为游客提供导游服务,每天有7个航班,6列火车.
思考1 该志愿者从济南到沈阳的方案可分几类?
答案 两类,即乘飞机、坐火车.
思考2 这几类方案中各有几种方法?
答案 第1类方案(乘飞机)有7种方法,第2类方案(坐火车)有6种方法.
思考3 该志愿者从济南到沈阳共有多少种不同的方法?
答案 共有7+6=13种不同的方法.
答案
1.完成一件事有两类不同的方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N= 种不同的方法.
2.完成一件事有n类不同的方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,…,在第n类方案中有mn种不同的方法,则完成这件事共有N= 种不同的方法.
m+n
m1+m2+…+mn
答案
知识点二 分步乘法计数原理
若这名志愿者从济南赶赴沈阳为游客提供导游服务,但需在北京停留,已知从济南到北京每天有7个航班,从北京到沈阳每天有6列火车.
思考1 该志愿者从济南到沈阳需要经历几个步骤?
答案 两个,即先乘飞机到北京,再坐火车到沈阳.
思考2 完成每一个步骤各有几种方法?
答案 第1个步骤有7种方法,第2个步骤有6种方法.
思考3 该志愿者从济南到沈阳共有多少种不同的方法?
答案 共有7×6=42种不同的方法.
答案
返回
1.完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N= 种不同的方法.
2.完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,…,做第n步有mn种不同的方法,则完成这件事共有N=
种不同的方法.
m×n
m1×m2×…×mn
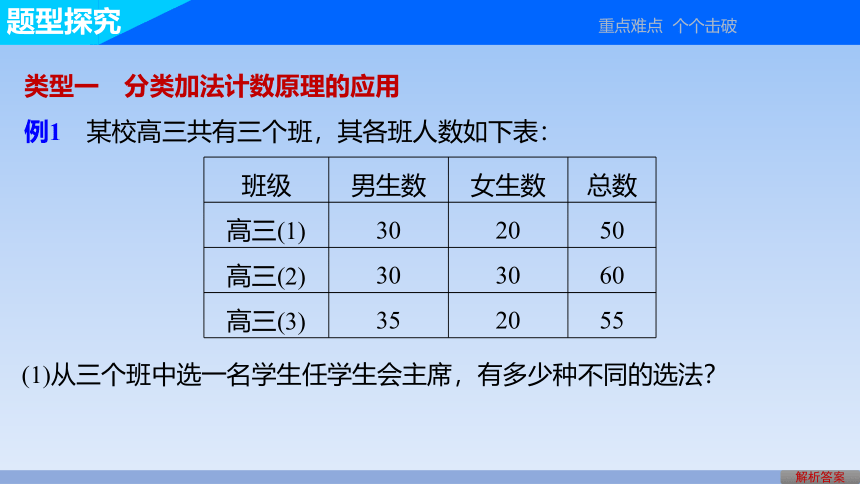
类型一 分类加法计数原理的应用
例1 某校高三共有三个班,其各班人数如下表:
解析答案
题型探究 重点难点 个个击破
班级 男生数 女生数 总数
高三(1) 30 20 50
高三(2) 30 30 60
高三(3) 35 20 55
(1)从三个班中选一名学生任学生会主席,有多少种不同的选法?
解 从三个班中任选一名学生,可分三类:
第1类,从高三(1)班任选一名学生,有50种不同选法;
第2类,从高三(2)班任选一名学生,有60种不同选法;
第3类,从高三(3)班任选一名学生,有55种不同选法.
由分类加法计数原理知,不同的选法共有N=50+60+55=165(种).
(2)从(1)班、(2)班男生中或从(3)班女生中选一名学生任学生会生活部部长,有多少种不同的选法?
解 由题设知共有三类:
第1类,从(1)班男生中任选一名学生,有30种不同选法;
第2类,从(2)班男生中任选一名学生,有30种不同选法;
第3类,从(3)班女生中任选一名学生,有20种不同选法.
由分类加法计数原理知,不同的选法共有N=30+30+20=80(种).
解析答案
反思与感悟
反思与感悟
1.应用分类加法计数原理时,完成这件事的n类方法是
相互独立的,无论哪种方案中的哪种方法,都可以独立完成这件事.
2.利用分类加法计数原理解题的一般思路
解析答案
跟踪训练1 如图,小圆点表示网络的结点,结点之间的连线表示它们由网线相连,连线上标注的数字表示该段网线单位时间内可以
通过的最大信息量.现从结点A向结点B传递信息,信息可沿
不同的路径同时传递.则单位时间内传递的最大信息量是___.
解析 若以网线为标准,则完成“从结点A向结点B传递信息”这件事也可分为四类,从而分解为若干个简单的问题后再各个击破.
分四类:第一类,网线为12→5→3,单位时间传递的最大信息量是3;
第二类,网线为12→6→4,单位时间传递的最大信息量是4;
第三类,网线为12→6→7,单位时间传递的最大信息量是6;
第四类,网线为12→8→6,单位时间传递的最大信息量是6.根据分类加法计数原理,单位时间内传递最大信息量是N=3+4+6+6=19.
19
解析答案
反思与感悟
类型二 分步乘法计数原理的应用
例2 从-2,-1,0,1,2,3这六个数字中任选3个不重复的数字作为二次函数y=ax2+bx+c的系数a,b,c,则可以组成抛物线的条数为____.
解析 由题意知a不能为0,
故a的值有5种选法;
b的值也有5种选法;
c的值有4种选法.
由分步乘法计数原理得:
5×5×4=100(条).
100
反思与感悟
1.应用分步乘法计数原理时,完成这件事情要分几个步骤,只有每个步骤都完成了,才算完成这件事情,每个步骤缺一不可.
2.利用分步乘法计数原理解题的一般思路:
(1)分步:将完成这件事的过程分成若干步;
(2)计数:求出每一步中的方法数;
(3)结论:将每一步中的方法数相乘得最终结果.
解析答案
跟踪训练2 从集合{0,1,2,3,5,7,11}中任取三个元素分别作为直线方程Ax+By+C=0中的A,B,C,所得直线经过坐标原点的有___条.
解析 该题实质上就是给A,B,C赋值.
但首先要搞清楚直线过原点所隐含的条件,即C=0,
所以,下面只需安排A,B.
从1,2,3,5,7,11这6个数中任取2个作为A,B的值,分为两步:第一步取一个数作为A,有6种;
第二步从剩下的5个数中取一个数作为B,有5种.
所以由分步乘法计数原理得:直线的条数为6×5=30.
30
解析答案
类型三 两个计数原理的综合应用
例3 某校高中三年级一班有优秀团员8人,二班有优秀团员10人,三班有优秀团员6人,学校组织他们去参观某爱国主义教育基地.
(1)推选1人为总负责人,有多少种不同的选法?
解 分三类,第一类是从一班的8名优秀团员中产生,共有8种不同的选法;
第二类是从二班的10名优秀团员中产生,共有10种不同的选法;
第三类是从三班的6名优秀团员中产生,共6种不同的选法,
由分类加法计数原理可得,共有N=8+10+6=24(种)不同的选法.
解析答案
(2)每班选1人为小组长,有多少种不同的选法?
解 分三步,第一步从一班的8名优秀团员中选1名组长,共有8种不同的选法,
第二步从二班的10名优秀团员中选1名组员,共10种不同的选法.
第三步是从三班的6名优秀团员中产生,共6种不同的选法,
由分步乘法计数原理可得:共有N=8×10×6=480(种)不同的选法.
解析答案
反思与感悟
(3)从他们中选出2个人管理生活,要求这2个人不同班,有多少种不同的选法?
解 分三类:每一类又分两步,第一类是从一班、二班的优秀团员中各选1人,有8×10种不同的选法;
第二类是从二班、三班的优秀团员中各选1人,有10×6种不同的选法,
第三类是从一班、三班的优秀团员中各选1人,有8×6种不同的选法,
因此,共有N=8×10+10×6+8×6=188(种)不同的选法.
反思与感悟
1.解题的关键是分清楚是“分类”还是“分步”,如问题(2)中,要求是每班各选1人为小组长,一班的8种不同选法中的任一种选法只能完成第一步,二班的选法也只能完成第二步,…,所以问题(2)是要用“分步”来解决问题.(3)中选出的2人来自不同的班级,又共有三个班,故应先分类,再分步方可完成.
2.分类讨论解决问题,必须思维清晰,保证分类标准的唯一性,这样才能保证分类不重复,不遗漏,运用两个原理解答时是先分类后分步还是先分步后分类,应视具体问题而定.
解析答案
返回
跟踪训练3 高艳有4件不同颜色的衬衣、3件不同花样的裙子,另有2套不同样式的连衣裙.“五一”劳动节需选择一套服装参加歌舞演出,则高艳不同的穿衣服的方式有___种.
解析 穿衣方式分两类:
第一步:不选连衣裙有4×3=12(种)方法.
第二步:选连衣裙有2种方法.
由分类加法计数原理知,共有12+2=14(种)方法.
14
1
2
3
解析答案
达标检测
4
1.某学生在书店发现3本好书,决定至少买其中的1本,则购买方法有
( )
A.3种 B.6种
C.7种 D.9种
解析 分3类,买1本书,买2本书,买3本书,各类的方法依次为3种,3种,1种,故购买方法有3+3+1=7(种).
5
C
解析答案
2.现有4件不同款式的上衣和3条不同颜色的长裤,如果一条长裤与一件上衣配成一套,则不同的配法种数为( )
A.7 B.12
C.64 D.81
解析 要完成配套,分两步:第1步,选上衣,从4件上衣中任选一件,有4种不同选法;
第2步,选长裤,从3条长裤中任选一条,有3种不同选法.
故共有4×3=12(种)不同的配法.
1
2
3
4
5
B
解析答案
3.把5本书全部借给3名学生,有_____种不同的借法.
解析 依题意,知每本书应借给三个人中的一个,
即每本书都有3种不同的借法,
由分步乘法计数原理,
得共有N=3×3×3×3×3=35=243(种)不同的借法.
1
2
3
4
5
243
解析答案
4.5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员参加团体比赛,则入选的3名队员中至少有一名老队员的选法有____种.(用数字作答)
解析 分为两类:两名老队员,一名新队员时,有3种选法;
两名新队员、一名老队员时,有2×3=6(种)选法,
即共有9种不同选法.
1
2
3
4
5
9
解析答案
5.某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语和日语的各一人,有多少种不同的选法?
解 依题意得,既会英语、又会日语的有:7+3-9=1(人),6人只会英语,2人只会日语,第一类:从只会英语的6人中选一人有6种方法,
此时,会日语的有2+1=3(种),
由分步乘法计数原理可得:N1=6×3=18(种).
第二类,不从只会英语的6人中选,只有1种方法,此时会日语的有2种,
由分步乘法计数原理可得:N2=1×2=2(种).
综上可知,共有18+2=20(种)不同的选法.
1
2
3
4
5
返回
规律与方法
1.使用两个原理解题的本质
2.利用两个计数原理解决实际问题的常用方法
§6.1 分类加法计数原理与分布乘法计数原理(一)
1.理解分类加法计数原理与分类乘法计数原理.
2.会用这两个原理分析和解决一些简单的实际计数问题.
问题导学
题型探究
达标检测
学习目标
答案
问题导学 新知探究 点点落实
知识点一 分类加法计数原理
第十二届全运会在中国辽宁盛大召开,一名志愿者从济南赶赴沈阳为游客提供导游服务,每天有7个航班,6列火车.
思考1 该志愿者从济南到沈阳的方案可分几类?
答案 两类,即乘飞机、坐火车.
思考2 这几类方案中各有几种方法?
答案 第1类方案(乘飞机)有7种方法,第2类方案(坐火车)有6种方法.
思考3 该志愿者从济南到沈阳共有多少种不同的方法?
答案 共有7+6=13种不同的方法.
答案
1.完成一件事有两类不同的方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N= 种不同的方法.
2.完成一件事有n类不同的方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,…,在第n类方案中有mn种不同的方法,则完成这件事共有N= 种不同的方法.
m+n
m1+m2+…+mn
答案
知识点二 分步乘法计数原理
若这名志愿者从济南赶赴沈阳为游客提供导游服务,但需在北京停留,已知从济南到北京每天有7个航班,从北京到沈阳每天有6列火车.
思考1 该志愿者从济南到沈阳需要经历几个步骤?
答案 两个,即先乘飞机到北京,再坐火车到沈阳.
思考2 完成每一个步骤各有几种方法?
答案 第1个步骤有7种方法,第2个步骤有6种方法.
思考3 该志愿者从济南到沈阳共有多少种不同的方法?
答案 共有7×6=42种不同的方法.
答案
返回
1.完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N= 种不同的方法.
2.完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,…,做第n步有mn种不同的方法,则完成这件事共有N=
种不同的方法.
m×n
m1×m2×…×mn
类型一 分类加法计数原理的应用
例1 某校高三共有三个班,其各班人数如下表:
解析答案
题型探究 重点难点 个个击破
班级 男生数 女生数 总数
高三(1) 30 20 50
高三(2) 30 30 60
高三(3) 35 20 55
(1)从三个班中选一名学生任学生会主席,有多少种不同的选法?
解 从三个班中任选一名学生,可分三类:
第1类,从高三(1)班任选一名学生,有50种不同选法;
第2类,从高三(2)班任选一名学生,有60种不同选法;
第3类,从高三(3)班任选一名学生,有55种不同选法.
由分类加法计数原理知,不同的选法共有N=50+60+55=165(种).
(2)从(1)班、(2)班男生中或从(3)班女生中选一名学生任学生会生活部部长,有多少种不同的选法?
解 由题设知共有三类:
第1类,从(1)班男生中任选一名学生,有30种不同选法;
第2类,从(2)班男生中任选一名学生,有30种不同选法;
第3类,从(3)班女生中任选一名学生,有20种不同选法.
由分类加法计数原理知,不同的选法共有N=30+30+20=80(种).
解析答案
反思与感悟
反思与感悟
1.应用分类加法计数原理时,完成这件事的n类方法是
相互独立的,无论哪种方案中的哪种方法,都可以独立完成这件事.
2.利用分类加法计数原理解题的一般思路
解析答案
跟踪训练1 如图,小圆点表示网络的结点,结点之间的连线表示它们由网线相连,连线上标注的数字表示该段网线单位时间内可以
通过的最大信息量.现从结点A向结点B传递信息,信息可沿
不同的路径同时传递.则单位时间内传递的最大信息量是___.
解析 若以网线为标准,则完成“从结点A向结点B传递信息”这件事也可分为四类,从而分解为若干个简单的问题后再各个击破.
分四类:第一类,网线为12→5→3,单位时间传递的最大信息量是3;
第二类,网线为12→6→4,单位时间传递的最大信息量是4;
第三类,网线为12→6→7,单位时间传递的最大信息量是6;
第四类,网线为12→8→6,单位时间传递的最大信息量是6.根据分类加法计数原理,单位时间内传递最大信息量是N=3+4+6+6=19.
19
解析答案
反思与感悟
类型二 分步乘法计数原理的应用
例2 从-2,-1,0,1,2,3这六个数字中任选3个不重复的数字作为二次函数y=ax2+bx+c的系数a,b,c,则可以组成抛物线的条数为____.
解析 由题意知a不能为0,
故a的值有5种选法;
b的值也有5种选法;
c的值有4种选法.
由分步乘法计数原理得:
5×5×4=100(条).
100
反思与感悟
1.应用分步乘法计数原理时,完成这件事情要分几个步骤,只有每个步骤都完成了,才算完成这件事情,每个步骤缺一不可.
2.利用分步乘法计数原理解题的一般思路:
(1)分步:将完成这件事的过程分成若干步;
(2)计数:求出每一步中的方法数;
(3)结论:将每一步中的方法数相乘得最终结果.
解析答案
跟踪训练2 从集合{0,1,2,3,5,7,11}中任取三个元素分别作为直线方程Ax+By+C=0中的A,B,C,所得直线经过坐标原点的有___条.
解析 该题实质上就是给A,B,C赋值.
但首先要搞清楚直线过原点所隐含的条件,即C=0,
所以,下面只需安排A,B.
从1,2,3,5,7,11这6个数中任取2个作为A,B的值,分为两步:第一步取一个数作为A,有6种;
第二步从剩下的5个数中取一个数作为B,有5种.
所以由分步乘法计数原理得:直线的条数为6×5=30.
30
解析答案
类型三 两个计数原理的综合应用
例3 某校高中三年级一班有优秀团员8人,二班有优秀团员10人,三班有优秀团员6人,学校组织他们去参观某爱国主义教育基地.
(1)推选1人为总负责人,有多少种不同的选法?
解 分三类,第一类是从一班的8名优秀团员中产生,共有8种不同的选法;
第二类是从二班的10名优秀团员中产生,共有10种不同的选法;
第三类是从三班的6名优秀团员中产生,共6种不同的选法,
由分类加法计数原理可得,共有N=8+10+6=24(种)不同的选法.
解析答案
(2)每班选1人为小组长,有多少种不同的选法?
解 分三步,第一步从一班的8名优秀团员中选1名组长,共有8种不同的选法,
第二步从二班的10名优秀团员中选1名组员,共10种不同的选法.
第三步是从三班的6名优秀团员中产生,共6种不同的选法,
由分步乘法计数原理可得:共有N=8×10×6=480(种)不同的选法.
解析答案
反思与感悟
(3)从他们中选出2个人管理生活,要求这2个人不同班,有多少种不同的选法?
解 分三类:每一类又分两步,第一类是从一班、二班的优秀团员中各选1人,有8×10种不同的选法;
第二类是从二班、三班的优秀团员中各选1人,有10×6种不同的选法,
第三类是从一班、三班的优秀团员中各选1人,有8×6种不同的选法,
因此,共有N=8×10+10×6+8×6=188(种)不同的选法.
反思与感悟
1.解题的关键是分清楚是“分类”还是“分步”,如问题(2)中,要求是每班各选1人为小组长,一班的8种不同选法中的任一种选法只能完成第一步,二班的选法也只能完成第二步,…,所以问题(2)是要用“分步”来解决问题.(3)中选出的2人来自不同的班级,又共有三个班,故应先分类,再分步方可完成.
2.分类讨论解决问题,必须思维清晰,保证分类标准的唯一性,这样才能保证分类不重复,不遗漏,运用两个原理解答时是先分类后分步还是先分步后分类,应视具体问题而定.
解析答案
返回
跟踪训练3 高艳有4件不同颜色的衬衣、3件不同花样的裙子,另有2套不同样式的连衣裙.“五一”劳动节需选择一套服装参加歌舞演出,则高艳不同的穿衣服的方式有___种.
解析 穿衣方式分两类:
第一步:不选连衣裙有4×3=12(种)方法.
第二步:选连衣裙有2种方法.
由分类加法计数原理知,共有12+2=14(种)方法.
14
1
2
3
解析答案
达标检测
4
1.某学生在书店发现3本好书,决定至少买其中的1本,则购买方法有
( )
A.3种 B.6种
C.7种 D.9种
解析 分3类,买1本书,买2本书,买3本书,各类的方法依次为3种,3种,1种,故购买方法有3+3+1=7(种).
5
C
解析答案
2.现有4件不同款式的上衣和3条不同颜色的长裤,如果一条长裤与一件上衣配成一套,则不同的配法种数为( )
A.7 B.12
C.64 D.81
解析 要完成配套,分两步:第1步,选上衣,从4件上衣中任选一件,有4种不同选法;
第2步,选长裤,从3条长裤中任选一条,有3种不同选法.
故共有4×3=12(种)不同的配法.
1
2
3
4
5
B
解析答案
3.把5本书全部借给3名学生,有_____种不同的借法.
解析 依题意,知每本书应借给三个人中的一个,
即每本书都有3种不同的借法,
由分步乘法计数原理,
得共有N=3×3×3×3×3=35=243(种)不同的借法.
1
2
3
4
5
243
解析答案
4.5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员参加团体比赛,则入选的3名队员中至少有一名老队员的选法有____种.(用数字作答)
解析 分为两类:两名老队员,一名新队员时,有3种选法;
两名新队员、一名老队员时,有2×3=6(种)选法,
即共有9种不同选法.
1
2
3
4
5
9
解析答案
5.某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语和日语的各一人,有多少种不同的选法?
解 依题意得,既会英语、又会日语的有:7+3-9=1(人),6人只会英语,2人只会日语,第一类:从只会英语的6人中选一人有6种方法,
此时,会日语的有2+1=3(种),
由分步乘法计数原理可得:N1=6×3=18(种).
第二类,不从只会英语的6人中选,只有1种方法,此时会日语的有2种,
由分步乘法计数原理可得:N2=1×2=2(种).
综上可知,共有18+2=20(种)不同的选法.
1
2
3
4
5
返回
规律与方法
1.使用两个原理解题的本质
2.利用两个计数原理解决实际问题的常用方法
