人教A版(2019)高中数学选择性必修第三册《分类加法与分步乘法计数原理---习题课》名师课件(共24张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册《分类加法与分步乘法计数原理---习题课》名师课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 449.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 20:11:45 | ||
图片预览








文档简介
(共24张PPT)
复习引入
分类加法原理:完成一件事有n类不同方案,在第一类方案中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法.那么完成这件事共有N=m1 +m2+…+mn种不同方法.完成这件事情的N类方法中,只需用一种方法就能完成这件事.
分步乘法计数原理:完成一件事有n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步中有mn种不同的方法.那么完成这件事共有N=m1m2…mn种不同方法.完成这件事情的n个步骤中,每个步骤都完成才能完成这件事.
分类加法计数原理和分步乘法计数原理的
共同点:
不同点:
分类加法计数原理与分类有关,
分步乘法计数原理与分步有关.
回答的都是有关做一件事的不同方法种数的问题
复习引入
加法原理 乘法原理
联系
区别一
完成一件事情共有n类办法,关键词是“分类”
完成一件事情,共分n个
步骤,关键词是“分步”
区别二
每类办法都能独立完成这件事情.
每一步得到的只是中间结果,任何一步都不能能独立完成这件事情,缺少任何一步也不能完成这件事情,只有每个步骤完成了,才能完成这件事情.
分类计数原理和分步计数原理,回答的都是关于完成一件事情的不同方法的种数的问题.
区别三
各类办法是互斥的、并列的、独立的
各步之间是相关联的
类类独立,步步关联
人教A版同步教材名师课件
分类加法与分步乘法计数原理
---习题课
典例讲解
例1、某班共有男生28名,女生20名,从该班选出学生代表参加校学代会.若学校分配给该班1名代表,有多少种不同的选法
选出1名代表有2类方式:
第1类是从男生中选出1名代表,有28种不同方法;
第2类是从女生中选出1名代表,有20种不同方法.
根据分类加法计数原理,共有不同的选法种数是28+20=48.
解析
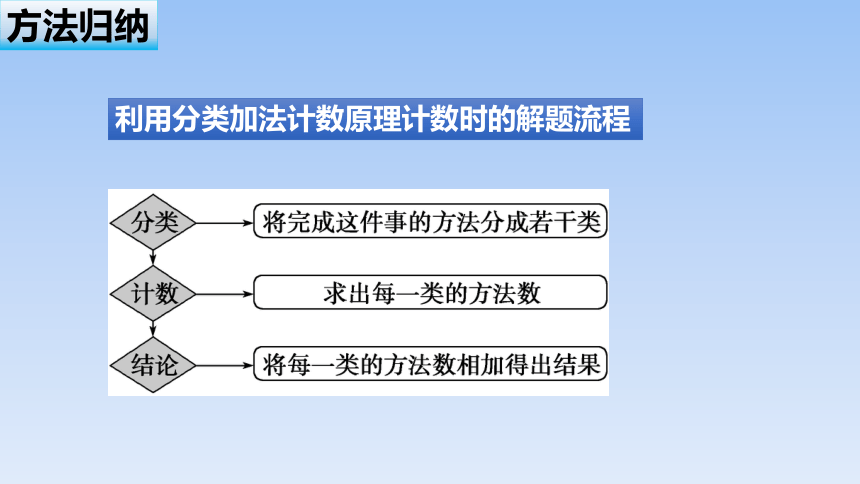
利用分类加法计数原理计数时的解题流程
方法归纳
变式训练
1.高二(1)班有学生50人,其中男生30人,女生20人;高二(2)班有学生60人,其中男生30人,女生30人;高二(3)班有学生55人,其中男生35人,女生20人.
(1)从高二(1)班或(2)班或(3)班中选一名学生任校学生会主席,有多少种不同的选法?
(2)从高二(1)班、(2)班男生中或从高二(3)班女生中选一名学生任校学生会体育部长,有多少种不同的选法?
(1)从高二(1)班中选一名学生任校学生会主席,有50种选法;从高二(2)班中选一名学生任校学生会主席,有60种选法;从高二(3)班中选一名学生任校学生会主席,有55种选法,由分类加法计数原理得,从高二(1)班或(2)班或(3)班中选一名学生任校学生会主席,有50+60+55=165种选法.
解析
变式训练
1.高二(1)班有学生50人,其中男生30人,女生20人;高二(2)班有学生60人,其中男生30人,女生30人;高二(3)班有学生55人,其中男生35人,女生20人.
(1)从高二(1)班或(2)班或(3)班中选一名学生任校学生会主席,有多少种不同的选法?
(2)从高二(1)班、(2)班男生中或从高二(3)班女生中选一名学生任校学生会体育部长,有多少种不同的选法?
解析
(2)从高二(1)班男生中选一名学生任校学生会体育部长有30种选法;从高二(2)班男生中选一名学生任校学生会体育部长有30种选法;从高二(3)班女生中选一名学生任校学生会体育部长有20种选法,由分类加法计数原理得,从高二(1)班、(2)班男生中或从高二(3)班女生中选一名学生任校学生会体育部长,不同的选法有30+30+20=80种.
例1、给程序模块命名,需要用3个字符,其中首字符要求用字母A~G或U~Z,后两个要求用数字1~9,最多可以给多少个程序命名
先计算首字符的选法.
由分类加法计数原理,首字符共有7+6=13种选法.
再计算后两个有9×9=81种选法;
由乘法计数原理有13×9×9=1 053(种).
∴最多可以给1 053个程序命名.
典例讲解
解析
(1)当涉及对象数目不大时,一般选用枚举法、树形图法、框图法或者图表法.
(2)当涉及对象数目很大时,一般有两种方法:
①直接使用分类加法计数原理或分步乘法计数原理.一般地,若抽取是有顺序的就按分步进行;若按对象特征抽取的,则按分类进行.
②间接法:去掉限制条件计算所有的抽取方法数,然后减去所有不符合条件的抽取方法数即可.
选(抽)取与分配问题的常见类型及其解法
方法归纳
1.设集合I={1,2,3,4,5},选择I的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有( )
A.50种 B.49种 C.48种 D.47种
B
按分类加法计数原理做如下讨论:
①当A中最大的数为1时,B可以是{2,3,4,5}的非空子集,即有24-1=15种方法;
②当A中最大的数为2时,A可以是{2}或{1,2},B可以是{3,4,5}的非空子集,即有2×(23-1)=14种方法.
③当A中最大的数为3时,A可以是{3},{1,3},{2,3},{1,2,3},B可以是{4,5}的非空子集,即有4×(22-1)=12种方法.
④当A中最大的数为4时,A可以是{4},{1,4},{2,4},{3,4},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4},B可以是{5},即有8×1=8种方法.
故共有15+14+12+8=49种方法.
变式训练
解析
例2、核糖核酸(RNA)分子是在生物细胞中发现的化学成分.一个RNA分子是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称为碱基的化学成分所占据.总共有4种不同的碱基,分别用A,C,G,U表示.在一个RNA分子中,各种碱基能够以任意次序出现,所以在任意一个位置上的碱基与其他位置上的碱基无关.假设有一类RNA分子由100个碱基组成,那么能有多少种不同的RNA分子
100个碱基组成的长链共有100个位置,如图所示.
从左到右依次在每一个位置中,从A,C,G,U中任选一个填入,每个位置有4种填充方法.根据分步乘法计数原理,长度为100的所有可能的不同RNA分子种数为
典例讲解
解析
解决元素可重复选取的计数问题时,首先搞清以谁为“主”,采用分步乘法计数原理求解,分步时,看哪类元素必须用完,就以该类元素的分步的依据进行分步.
方法归纳
2.用0,1,2,3,4五个数字.
(1)可以排出多少个三位数字的电话号码
(2)可以排成多少个三位数
(3)可以排成多少个能被2整除的无重复数字的三位数
(1)三位数字的电话号码,首位可以是0,数字也可以重复,每个位置都有5种排法,共有5×5×5=53=125(种).
(2)三位数的首位不能为0,但可以有重复数字,首先考虑首位的排法,除0外共有4种方法,第二、三位可以排0,因此,共有4×5×5=100(种).
(3)被2整除的数即偶数,末位数字可取0,2,4,因此,可以分两类,一类是末位数字是0,则有4×3=12种排法;一类是末位数字不是0,则末位有2种排法,即2或4,再排首位,因0不能在首位,所以有3种排法,十位有3种排法,因此有2×3×3=18种排法.因而有12+18=30种排法.即可以排成30个能被2整除的无重复数字的三位数.
变式训练
解析
例3、随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需要扩容.交通管理部门出台了一种汽车牌照组成办法,每一个汽车牌照都必须有3个不重复的英文字母和3个不重复的阿拉伯数字,并且3个字母必须合成一组出现,3个数字也必须合成一组出现.那么这种办法共能给多少辆汽车上牌照
将汽车牌照分为两类,一类的字母组合在左,另一类的字母组合在右.
字母组合在左时,分6个步骤确定一个牌照的字母和数字:
第1步,从26个字母中选1个,放在首位,有26种选法;
第2步,从剩下的25个字母中选1个,放在第2位,有25种选法;
第3步,从剩下的24个字母中选1个,放在第3位,有24种选法;
第4步,从10个数字中选1个,放在第4位,有10种选法;
第5步,从剩下的9个数字中选1个,放在第5位,有9种选法;
第6步,从剩下的8个数字中选1个,放在第6位,有8种选法.
典例讲解
解析
例3、随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需要扩容.交通管理部门出台了一种汽车牌照组成办法,每一个汽车牌照都必须有3个不重复的英文字母和3个不重复的阿拉伯数字,并且3个字母必须合成一组出现,3个数字也必须合成一组出现.那么这种办法共能给多少辆汽车上牌照
根据分步乘法计数原理,字母组合在左的牌照个数为
26×25×24×10×9×8=11 232 000.
同理,字母组合在右的牌照个数也为11 232 000.
所以,共能给11 232 000+11 232 000=22 464 000辆汽车上牌照.
典例讲解
解析
(1)对于有些计数问题的解决,对它们既需要进行“分类”,又需要进行“分步”,那么此时就要注意综合运用两个原理来解决问题.解决这类问题,首先要明确是先“分类”后“分步”,还是先“分步”后“分类”;其次,在“分类”和“分步”的过程中,均要确定明确的分类标准和分步程序.
(2)对于有些计数问题,我们既可以用分类加法计数原理解决问题,也可以用分步乘法计数原理来解决问题,此时,则要注意权衡用哪种方法解决问题较为简单.
方法归纳
3.现有5幅不同的国画,2幅不同的油画,7幅不同的水彩画.
(1)从中任选一幅画布置房间,有几种不同的选法
(2)从这些国画、油画、水彩画中各选一幅布置房间,有几种不同的选法
(3)从这些画中选出两幅不同种类的画布置房间,有几种不同的选法
(1)分为三类:从国画中选,有5种不同的选法;从油画中选,有2种不同的选法;从水彩画中选,有7种不同的选法.根据分类加法计数原理共有5+2+7=14种不同的选法.
(2)分为三步:国画、油画、水彩画各有5种、2种、7种不同的选法,根据分步乘法计数原理,共有5×2×7=70种不同的选法.
(3)分为三类:第一类是一幅选自国画,一幅选自油画.由分步乘法计数原理知,有5×2=10种不同的选法.
第二类是一幅选自国画,一幅选自水彩画,有5×7=35种不同的选法.
第三类是一幅选自油画,一幅选自水彩画,有2×7=14种不同的选法.
所以有10+35+14=59种不同的选法.
变式训练
解析
例4、3个人要坐在一排8个空座位上,若每个人左右都有空座位,不同的坐法有多少种?
3个人在一排8个空座位上坐下后,只剩下5个空座位,我们可以构造这样的解题过程,依次将3个人连同他的座位逐个地插入5个空座位形成的空座位当中去.由于每人左右都要有空位子,因此将第一个人连同他的座位插入时,不能插在两边,所以有4种插法[如图中的(1)到(2)];
然后将第二个人连同他的座位插入时,只有3种插法了[如图中的(2)到(3)];
最后将第三个人连同他的座位插入时,只有2种插入的方法了[如图中的(3)到(4)].
这时,我们再根据分步乘法计数原理,可以得到插入的不同的方法共有4×3×2=24(种).
典例讲解
解析
本题用“○”表示没有坐人的空位,用“□”表示已经坐人的位置,画图分析为我们构建分步乘法计数原理的模型铺平了道路.横型法就是通过构建相关图形,利用形象、直观的图形来构建两个原理的模型.模型法不仅可以帮助我们准确理解题意,而且还可以帮助我们有效地分析问题,从而建立起两个原理的模型,使问题顺利地解决.
方法归纳
例5、如图,花坛内有5个花池,有5种不同颜色的花卉可供栽种,每个花池内只能栽种相同颜色的花卉,相邻两池的花卉颜色不同,求最多有多少种栽种方案.
由题意知,最少用三种颜色的花卉,按照花卉的颜色可分为
三种方案,即用三种颜色,四种颜色,五种颜色.
①当用三种颜色时,花池2,4栽同种颜色的花卉,有5种方案,
花池3,5栽同种颜色的花卉,有4种方案,花池1有3种栽种方案,由分步乘法计数原理知有5×4×3=60种方案;
典例讲解
解析
例5、如图,花坛内有5个花池,有5种不同颜色的花卉可供栽种,每个花池内只能栽种相同颜色的花卉,相邻两池的花卉颜色不同,求最多有多少种栽种方案.
②当用四种颜色时,则花池2,4栽同种颜色的花卉,或花池3,5栽同种颜色的花卉.
若花池2,4栽同种颜色的花卉,有5种方案,花池3有4种栽种方案,花池5有3种栽种方案,花池1有2种栽种方案,
由分步乘法计数原理得5×4×3×2=120种栽种方案;若花池3,5栽同种颜色的花卉,同理得也有5×4×3×2=120种栽种方案;
再由分类加法计数原理共有120+120=240种栽种方案;
典例讲解
解析
例5、如图,花坛内有5个花池,有5种不同颜色的花卉可供栽种,每个花池内只能栽种相同颜色的花卉,相邻两池的花卉颜色不同,求最多有多少种栽种方案.
典例讲解
解析
③当用五种颜色时,花池1有5种栽种方案,花池2有4种栽种方案,花池3有3种栽种方案,花池4有2种栽种方案,花池5有1种栽种方案,由分步乘法计数原理得5×4×3×2×1=120种栽种方案.
根据分类加法计数原理得共有60+240+120=420种栽种方案.
故最多有420种栽种方案.
(2)解决涂色(种植)问题的关注点及技巧
特别关注图形的特征,有多少块,用多少种颜色,如果图形不是很规则,往往从某一块出发进行分步涂色;如果图形具有一定的对称性,那么先对涂色方案进行分类,每一类再分步,如本例花池2与4,3与5对称,可涂相同颜色.
(1)解决本题需注意以三个关键步骤:
方法归纳
作 业
P12习题6.1:9、10
复习引入
分类加法原理:完成一件事有n类不同方案,在第一类方案中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法.那么完成这件事共有N=m1 +m2+…+mn种不同方法.完成这件事情的N类方法中,只需用一种方法就能完成这件事.
分步乘法计数原理:完成一件事有n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步中有mn种不同的方法.那么完成这件事共有N=m1m2…mn种不同方法.完成这件事情的n个步骤中,每个步骤都完成才能完成这件事.
分类加法计数原理和分步乘法计数原理的
共同点:
不同点:
分类加法计数原理与分类有关,
分步乘法计数原理与分步有关.
回答的都是有关做一件事的不同方法种数的问题
复习引入
加法原理 乘法原理
联系
区别一
完成一件事情共有n类办法,关键词是“分类”
完成一件事情,共分n个
步骤,关键词是“分步”
区别二
每类办法都能独立完成这件事情.
每一步得到的只是中间结果,任何一步都不能能独立完成这件事情,缺少任何一步也不能完成这件事情,只有每个步骤完成了,才能完成这件事情.
分类计数原理和分步计数原理,回答的都是关于完成一件事情的不同方法的种数的问题.
区别三
各类办法是互斥的、并列的、独立的
各步之间是相关联的
类类独立,步步关联
人教A版同步教材名师课件
分类加法与分步乘法计数原理
---习题课
典例讲解
例1、某班共有男生28名,女生20名,从该班选出学生代表参加校学代会.若学校分配给该班1名代表,有多少种不同的选法
选出1名代表有2类方式:
第1类是从男生中选出1名代表,有28种不同方法;
第2类是从女生中选出1名代表,有20种不同方法.
根据分类加法计数原理,共有不同的选法种数是28+20=48.
解析
利用分类加法计数原理计数时的解题流程
方法归纳
变式训练
1.高二(1)班有学生50人,其中男生30人,女生20人;高二(2)班有学生60人,其中男生30人,女生30人;高二(3)班有学生55人,其中男生35人,女生20人.
(1)从高二(1)班或(2)班或(3)班中选一名学生任校学生会主席,有多少种不同的选法?
(2)从高二(1)班、(2)班男生中或从高二(3)班女生中选一名学生任校学生会体育部长,有多少种不同的选法?
(1)从高二(1)班中选一名学生任校学生会主席,有50种选法;从高二(2)班中选一名学生任校学生会主席,有60种选法;从高二(3)班中选一名学生任校学生会主席,有55种选法,由分类加法计数原理得,从高二(1)班或(2)班或(3)班中选一名学生任校学生会主席,有50+60+55=165种选法.
解析
变式训练
1.高二(1)班有学生50人,其中男生30人,女生20人;高二(2)班有学生60人,其中男生30人,女生30人;高二(3)班有学生55人,其中男生35人,女生20人.
(1)从高二(1)班或(2)班或(3)班中选一名学生任校学生会主席,有多少种不同的选法?
(2)从高二(1)班、(2)班男生中或从高二(3)班女生中选一名学生任校学生会体育部长,有多少种不同的选法?
解析
(2)从高二(1)班男生中选一名学生任校学生会体育部长有30种选法;从高二(2)班男生中选一名学生任校学生会体育部长有30种选法;从高二(3)班女生中选一名学生任校学生会体育部长有20种选法,由分类加法计数原理得,从高二(1)班、(2)班男生中或从高二(3)班女生中选一名学生任校学生会体育部长,不同的选法有30+30+20=80种.
例1、给程序模块命名,需要用3个字符,其中首字符要求用字母A~G或U~Z,后两个要求用数字1~9,最多可以给多少个程序命名
先计算首字符的选法.
由分类加法计数原理,首字符共有7+6=13种选法.
再计算后两个有9×9=81种选法;
由乘法计数原理有13×9×9=1 053(种).
∴最多可以给1 053个程序命名.
典例讲解
解析
(1)当涉及对象数目不大时,一般选用枚举法、树形图法、框图法或者图表法.
(2)当涉及对象数目很大时,一般有两种方法:
①直接使用分类加法计数原理或分步乘法计数原理.一般地,若抽取是有顺序的就按分步进行;若按对象特征抽取的,则按分类进行.
②间接法:去掉限制条件计算所有的抽取方法数,然后减去所有不符合条件的抽取方法数即可.
选(抽)取与分配问题的常见类型及其解法
方法归纳
1.设集合I={1,2,3,4,5},选择I的两个非空子集A和B,要使B中最小的数大于A中最大的数,则不同的选择方法共有( )
A.50种 B.49种 C.48种 D.47种
B
按分类加法计数原理做如下讨论:
①当A中最大的数为1时,B可以是{2,3,4,5}的非空子集,即有24-1=15种方法;
②当A中最大的数为2时,A可以是{2}或{1,2},B可以是{3,4,5}的非空子集,即有2×(23-1)=14种方法.
③当A中最大的数为3时,A可以是{3},{1,3},{2,3},{1,2,3},B可以是{4,5}的非空子集,即有4×(22-1)=12种方法.
④当A中最大的数为4时,A可以是{4},{1,4},{2,4},{3,4},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4},B可以是{5},即有8×1=8种方法.
故共有15+14+12+8=49种方法.
变式训练
解析
例2、核糖核酸(RNA)分子是在生物细胞中发现的化学成分.一个RNA分子是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称为碱基的化学成分所占据.总共有4种不同的碱基,分别用A,C,G,U表示.在一个RNA分子中,各种碱基能够以任意次序出现,所以在任意一个位置上的碱基与其他位置上的碱基无关.假设有一类RNA分子由100个碱基组成,那么能有多少种不同的RNA分子
100个碱基组成的长链共有100个位置,如图所示.
从左到右依次在每一个位置中,从A,C,G,U中任选一个填入,每个位置有4种填充方法.根据分步乘法计数原理,长度为100的所有可能的不同RNA分子种数为
典例讲解
解析
解决元素可重复选取的计数问题时,首先搞清以谁为“主”,采用分步乘法计数原理求解,分步时,看哪类元素必须用完,就以该类元素的分步的依据进行分步.
方法归纳
2.用0,1,2,3,4五个数字.
(1)可以排出多少个三位数字的电话号码
(2)可以排成多少个三位数
(3)可以排成多少个能被2整除的无重复数字的三位数
(1)三位数字的电话号码,首位可以是0,数字也可以重复,每个位置都有5种排法,共有5×5×5=53=125(种).
(2)三位数的首位不能为0,但可以有重复数字,首先考虑首位的排法,除0外共有4种方法,第二、三位可以排0,因此,共有4×5×5=100(种).
(3)被2整除的数即偶数,末位数字可取0,2,4,因此,可以分两类,一类是末位数字是0,则有4×3=12种排法;一类是末位数字不是0,则末位有2种排法,即2或4,再排首位,因0不能在首位,所以有3种排法,十位有3种排法,因此有2×3×3=18种排法.因而有12+18=30种排法.即可以排成30个能被2整除的无重复数字的三位数.
变式训练
解析
例3、随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需要扩容.交通管理部门出台了一种汽车牌照组成办法,每一个汽车牌照都必须有3个不重复的英文字母和3个不重复的阿拉伯数字,并且3个字母必须合成一组出现,3个数字也必须合成一组出现.那么这种办法共能给多少辆汽车上牌照
将汽车牌照分为两类,一类的字母组合在左,另一类的字母组合在右.
字母组合在左时,分6个步骤确定一个牌照的字母和数字:
第1步,从26个字母中选1个,放在首位,有26种选法;
第2步,从剩下的25个字母中选1个,放在第2位,有25种选法;
第3步,从剩下的24个字母中选1个,放在第3位,有24种选法;
第4步,从10个数字中选1个,放在第4位,有10种选法;
第5步,从剩下的9个数字中选1个,放在第5位,有9种选法;
第6步,从剩下的8个数字中选1个,放在第6位,有8种选法.
典例讲解
解析
例3、随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需要扩容.交通管理部门出台了一种汽车牌照组成办法,每一个汽车牌照都必须有3个不重复的英文字母和3个不重复的阿拉伯数字,并且3个字母必须合成一组出现,3个数字也必须合成一组出现.那么这种办法共能给多少辆汽车上牌照
根据分步乘法计数原理,字母组合在左的牌照个数为
26×25×24×10×9×8=11 232 000.
同理,字母组合在右的牌照个数也为11 232 000.
所以,共能给11 232 000+11 232 000=22 464 000辆汽车上牌照.
典例讲解
解析
(1)对于有些计数问题的解决,对它们既需要进行“分类”,又需要进行“分步”,那么此时就要注意综合运用两个原理来解决问题.解决这类问题,首先要明确是先“分类”后“分步”,还是先“分步”后“分类”;其次,在“分类”和“分步”的过程中,均要确定明确的分类标准和分步程序.
(2)对于有些计数问题,我们既可以用分类加法计数原理解决问题,也可以用分步乘法计数原理来解决问题,此时,则要注意权衡用哪种方法解决问题较为简单.
方法归纳
3.现有5幅不同的国画,2幅不同的油画,7幅不同的水彩画.
(1)从中任选一幅画布置房间,有几种不同的选法
(2)从这些国画、油画、水彩画中各选一幅布置房间,有几种不同的选法
(3)从这些画中选出两幅不同种类的画布置房间,有几种不同的选法
(1)分为三类:从国画中选,有5种不同的选法;从油画中选,有2种不同的选法;从水彩画中选,有7种不同的选法.根据分类加法计数原理共有5+2+7=14种不同的选法.
(2)分为三步:国画、油画、水彩画各有5种、2种、7种不同的选法,根据分步乘法计数原理,共有5×2×7=70种不同的选法.
(3)分为三类:第一类是一幅选自国画,一幅选自油画.由分步乘法计数原理知,有5×2=10种不同的选法.
第二类是一幅选自国画,一幅选自水彩画,有5×7=35种不同的选法.
第三类是一幅选自油画,一幅选自水彩画,有2×7=14种不同的选法.
所以有10+35+14=59种不同的选法.
变式训练
解析
例4、3个人要坐在一排8个空座位上,若每个人左右都有空座位,不同的坐法有多少种?
3个人在一排8个空座位上坐下后,只剩下5个空座位,我们可以构造这样的解题过程,依次将3个人连同他的座位逐个地插入5个空座位形成的空座位当中去.由于每人左右都要有空位子,因此将第一个人连同他的座位插入时,不能插在两边,所以有4种插法[如图中的(1)到(2)];
然后将第二个人连同他的座位插入时,只有3种插法了[如图中的(2)到(3)];
最后将第三个人连同他的座位插入时,只有2种插入的方法了[如图中的(3)到(4)].
这时,我们再根据分步乘法计数原理,可以得到插入的不同的方法共有4×3×2=24(种).
典例讲解
解析
本题用“○”表示没有坐人的空位,用“□”表示已经坐人的位置,画图分析为我们构建分步乘法计数原理的模型铺平了道路.横型法就是通过构建相关图形,利用形象、直观的图形来构建两个原理的模型.模型法不仅可以帮助我们准确理解题意,而且还可以帮助我们有效地分析问题,从而建立起两个原理的模型,使问题顺利地解决.
方法归纳
例5、如图,花坛内有5个花池,有5种不同颜色的花卉可供栽种,每个花池内只能栽种相同颜色的花卉,相邻两池的花卉颜色不同,求最多有多少种栽种方案.
由题意知,最少用三种颜色的花卉,按照花卉的颜色可分为
三种方案,即用三种颜色,四种颜色,五种颜色.
①当用三种颜色时,花池2,4栽同种颜色的花卉,有5种方案,
花池3,5栽同种颜色的花卉,有4种方案,花池1有3种栽种方案,由分步乘法计数原理知有5×4×3=60种方案;
典例讲解
解析
例5、如图,花坛内有5个花池,有5种不同颜色的花卉可供栽种,每个花池内只能栽种相同颜色的花卉,相邻两池的花卉颜色不同,求最多有多少种栽种方案.
②当用四种颜色时,则花池2,4栽同种颜色的花卉,或花池3,5栽同种颜色的花卉.
若花池2,4栽同种颜色的花卉,有5种方案,花池3有4种栽种方案,花池5有3种栽种方案,花池1有2种栽种方案,
由分步乘法计数原理得5×4×3×2=120种栽种方案;若花池3,5栽同种颜色的花卉,同理得也有5×4×3×2=120种栽种方案;
再由分类加法计数原理共有120+120=240种栽种方案;
典例讲解
解析
例5、如图,花坛内有5个花池,有5种不同颜色的花卉可供栽种,每个花池内只能栽种相同颜色的花卉,相邻两池的花卉颜色不同,求最多有多少种栽种方案.
典例讲解
解析
③当用五种颜色时,花池1有5种栽种方案,花池2有4种栽种方案,花池3有3种栽种方案,花池4有2种栽种方案,花池5有1种栽种方案,由分步乘法计数原理得5×4×3×2×1=120种栽种方案.
根据分类加法计数原理得共有60+240+120=420种栽种方案.
故最多有420种栽种方案.
(2)解决涂色(种植)问题的关注点及技巧
特别关注图形的特征,有多少块,用多少种颜色,如果图形不是很规则,往往从某一块出发进行分步涂色;如果图形具有一定的对称性,那么先对涂色方案进行分类,每一类再分步,如本例花池2与4,3与5对称,可涂相同颜色.
(1)解决本题需注意以三个关键步骤:
方法归纳
作 业
P12习题6.1:9、10
