1.1.2锐角三角函数 课件(共23张PPT)
文档属性
| 名称 | 1.1.2锐角三角函数 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 19:04:59 | ||
图片预览




文档简介
(共23张PPT)
1.1.2锐角三角函数
北师大版 九年级 下册
教学目标
教学目标: 1、能利用相似的直角三角形,探索并认识锐角三角函数——正弦、余弦,理解锐角的正弦与余弦和梯子倾斜程度的关系.
2、能够用sinA,cosA表示直角三角形中直角边与斜边的比,能够用正弦、余弦进行简单的计算.
教学重点: 能利用相似的直角三角形,探索并认识锐角三角函数——正弦、余弦,理解锐角的正弦与余弦和梯子倾斜程度的关系.
教学难点: 能够用sinA,cosA表示直角三角形中直角边与斜边的比,能够用正弦、余弦进行简单的计算.
新知导入
情境引入
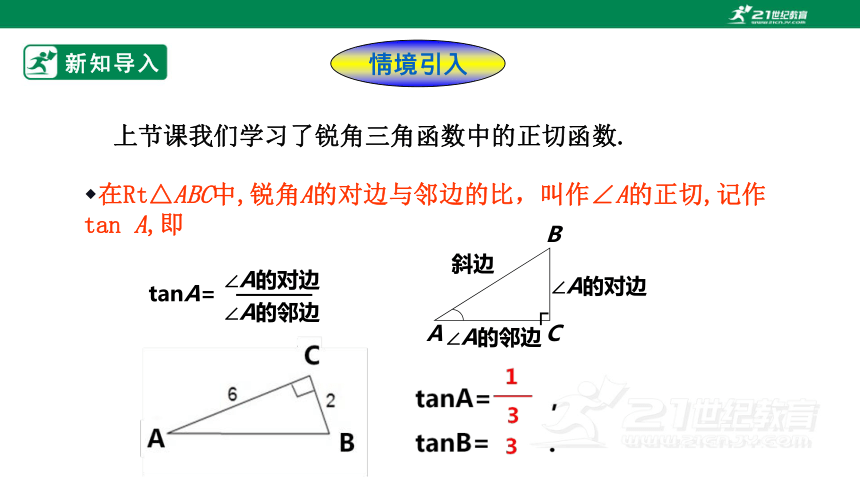
在Rt△ABC中,锐角A的对边与邻边的比,叫作∠A的正切,记作tan A,即
A
B
C
∠A的对边
∠A的邻边
┌
斜边
上节课我们学习了锐角三角函数中的正切函数.
tanA=
∠A的对边
∠A的邻边
新知讲解
合作学习
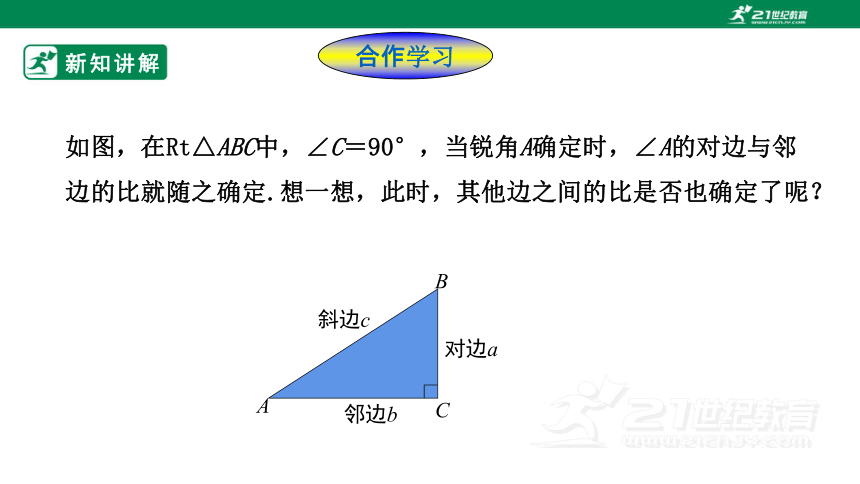
如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与邻边的比就随之确定.想一想,此时,其他边之间的比是否也确定了呢?
A
B
C
邻边b
对边a
斜边c
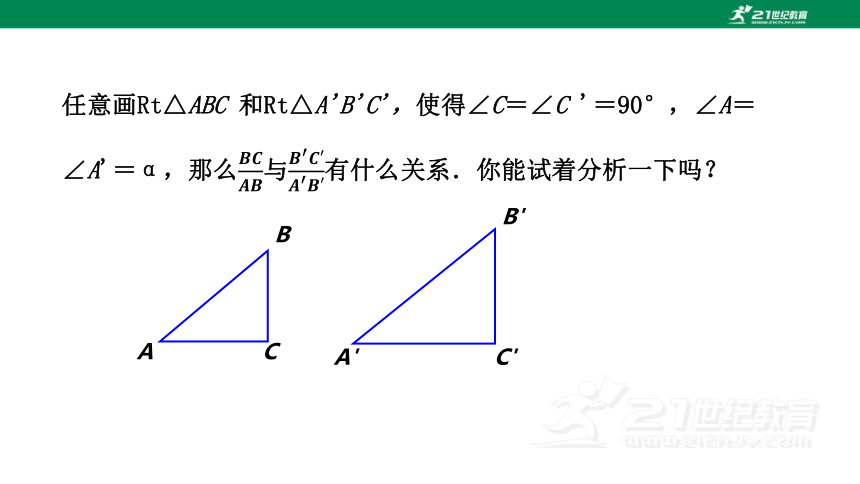
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C '=90°,∠A=∠A'=α,那么与有什么关系.你能试着分析一下吗?
A
B
C
A'
B'
C'
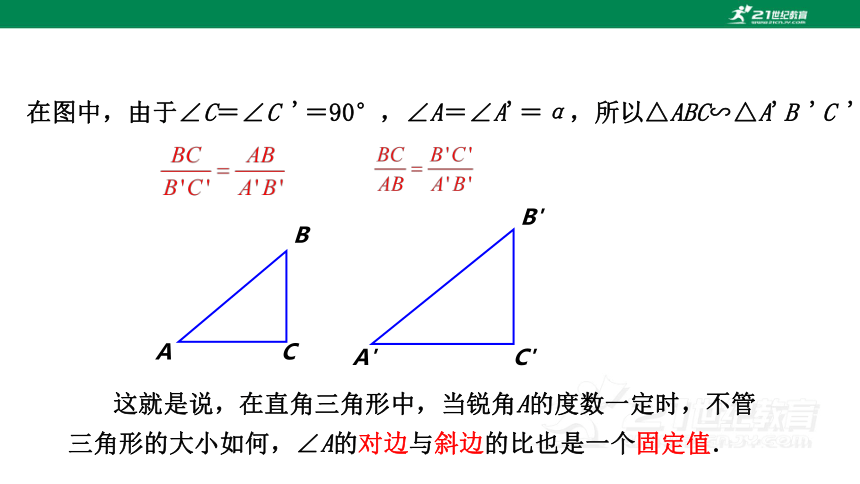
在图中,由于∠C=∠C '=90°,∠A=∠A'=α,所以△ABC∽△A'B 'C '
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
A
B
C
A'
B'
C'
提炼概念
在Rt△ABC中,锐角A的对边与斜边的比叫作∠A的正弦,记作sin A,即
在Rt△ABC中,锐角A的邻边与斜边的比叫作∠A的余弦,记作cos A,即
A
B
C
∠A的对边
∠A的邻边
┌
斜边
cos A=
sin A=
锐角A的正弦、余弦和正切都是∠A的三角函数.
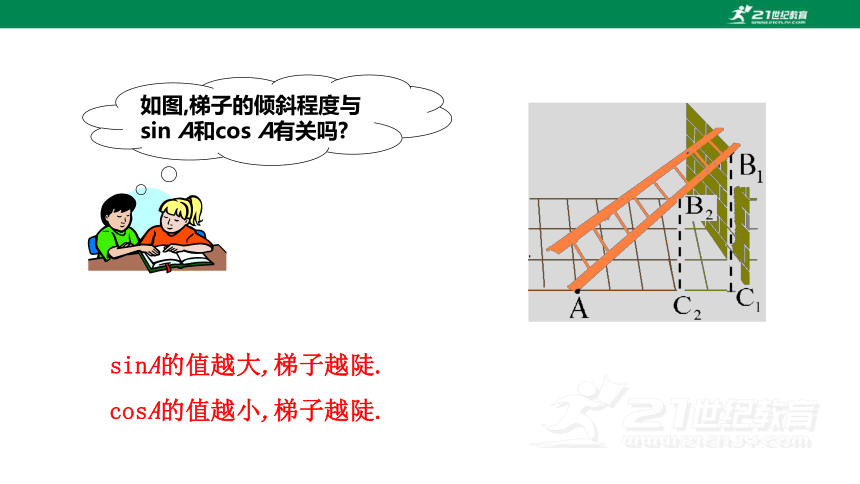
sinA的值越大,梯子越陡.
cosA的值越小,梯子越陡.
如图,梯子的倾斜程度与sin A和cos A有关吗
1.1.sin A, cos A, tan A是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sin A, cos A, tan A是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.sin A, cos A, tan A是一个比值. 注意比的顺序, 且sinA, cosA, tanA均﹥0,无单位.
4.sin A, cos A, tan A的大小只与∠A的大小有关,而与直角三角形的边长无关.
典例精讲
例2 如图,在Rt△ABC中,∠B=90 °,AC=200,sinA=0.6,求BC的长.
A
B
C
解: 在Rt △ABC中,sinA=
∴BC=AC·sinA=200×0.6=120
┐
A
B
C
如图,在Rt△ABC中,∠C=90°, AC=10,cosA=,AB等于多少? sinB 呢?
解:∵cosA=
∴AB=
∴sinB=
做一做
归纳概念
思考: 在Rt△ABC中, sin A和cos B 有什么关系
我们学习的锐角三角函数(直角三角形边角关系的函数)共有以下三个:
tanA=
sinA=
cosA=
A
B
C
∠A的对边
∠A的邻边
┌
斜边
sin A=cos B
课堂练习
1.在Rt△ABC中,∠C=90°,则下列式子一定成立的是( )
A.sinA=sinB B.cosA=cosB
C.tanA=tanB D.sinA=cosB
D
2. 如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A. sinA的值越小,梯子越陡 B. cosA的值越小,梯子越陡
C. tanA的值越小,梯子越陡 D. 陡缓程度与∠A的函数值无关
B
3.在Rt△ABC中,∠C=90°,sinA= ,则tanB的值为_________.
5
12
4.如图,在Rt△ABC中,∠C=90°,cosA= ,
求sinA、tanA的值.
A
B
C
设AC=15k,则AB=17k
5.某商场为方便消费者购物,准备将原来的阶梯式
自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动
扶梯AB长为10m,坡角∠ABD为30°;改造后的斜坡式自动扶梯
的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度,
(结果精确到0.lm).
温馨提示:sin15°≈0.26,cosl5°≈0.97,tan15°≈0.27)
解:在Rt△ABD中,∠ABD=30°,AB=10m,
∴AD=ABsin∠ABD=10×sin30°=5,
在Rt△ACD中,
∠ACD=15°, sin∠ACD=
AC
AD
∴AC= = ≈ ≈19.2m
sin∠ACD
AD
sin15°
5
0.26
5
答:改造后的斜坡式自动扶梯AC的长度约为19.2米.
6.如图,在正方形ABCD中,M是AD的中点,BE=3AE,求sin∠ECM.
解:设正方形ABCD的边长为4x,∵M是AD的中点,BE=3AE,
∴AM=DM=2x,AE=x,BE=3x.
由勾股定理可知,
A
M
E
D
B
C
∴EM2=AM2+AE2=(2x)2+x2=5x2
CM2=DM2+DC2=(2x)2+(4x)2=20x2
EC2=BC2+BE2=(4x)2+(3x)2=25x2
∴ EC2=EM2+CM2
由勾股定理逆定理可知,△EMC为直角三角形.
A
M
E
D
B
C
课堂总结
1.在Rt△ABC中
2.梯子的倾斜程度与sinA和cosA的关系:
sinA的值越大,梯子越陡;
cosA的值越小,梯子越陡.
sinA=
c
a
=
cosA=
c
b
=
sinA=cosB
A
B
C
∠A的对边
∠A的邻边
┌
斜边
a
c
b
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.1.2锐角三角函数
北师大版 九年级 下册
教学目标
教学目标: 1、能利用相似的直角三角形,探索并认识锐角三角函数——正弦、余弦,理解锐角的正弦与余弦和梯子倾斜程度的关系.
2、能够用sinA,cosA表示直角三角形中直角边与斜边的比,能够用正弦、余弦进行简单的计算.
教学重点: 能利用相似的直角三角形,探索并认识锐角三角函数——正弦、余弦,理解锐角的正弦与余弦和梯子倾斜程度的关系.
教学难点: 能够用sinA,cosA表示直角三角形中直角边与斜边的比,能够用正弦、余弦进行简单的计算.
新知导入
情境引入
在Rt△ABC中,锐角A的对边与邻边的比,叫作∠A的正切,记作tan A,即
A
B
C
∠A的对边
∠A的邻边
┌
斜边
上节课我们学习了锐角三角函数中的正切函数.
tanA=
∠A的对边
∠A的邻边
新知讲解
合作学习
如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与邻边的比就随之确定.想一想,此时,其他边之间的比是否也确定了呢?
A
B
C
邻边b
对边a
斜边c
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C '=90°,∠A=∠A'=α,那么与有什么关系.你能试着分析一下吗?
A
B
C
A'
B'
C'
在图中,由于∠C=∠C '=90°,∠A=∠A'=α,所以△ABC∽△A'B 'C '
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
A
B
C
A'
B'
C'
提炼概念
在Rt△ABC中,锐角A的对边与斜边的比叫作∠A的正弦,记作sin A,即
在Rt△ABC中,锐角A的邻边与斜边的比叫作∠A的余弦,记作cos A,即
A
B
C
∠A的对边
∠A的邻边
┌
斜边
cos A=
sin A=
锐角A的正弦、余弦和正切都是∠A的三角函数.
sinA的值越大,梯子越陡.
cosA的值越小,梯子越陡.
如图,梯子的倾斜程度与sin A和cos A有关吗
1.1.sin A, cos A, tan A是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sin A, cos A, tan A是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.sin A, cos A, tan A是一个比值. 注意比的顺序, 且sinA, cosA, tanA均﹥0,无单位.
4.sin A, cos A, tan A的大小只与∠A的大小有关,而与直角三角形的边长无关.
典例精讲
例2 如图,在Rt△ABC中,∠B=90 °,AC=200,sinA=0.6,求BC的长.
A
B
C
解: 在Rt △ABC中,sinA=
∴BC=AC·sinA=200×0.6=120
┐
A
B
C
如图,在Rt△ABC中,∠C=90°, AC=10,cosA=,AB等于多少? sinB 呢?
解:∵cosA=
∴AB=
∴sinB=
做一做
归纳概念
思考: 在Rt△ABC中, sin A和cos B 有什么关系
我们学习的锐角三角函数(直角三角形边角关系的函数)共有以下三个:
tanA=
sinA=
cosA=
A
B
C
∠A的对边
∠A的邻边
┌
斜边
sin A=cos B
课堂练习
1.在Rt△ABC中,∠C=90°,则下列式子一定成立的是( )
A.sinA=sinB B.cosA=cosB
C.tanA=tanB D.sinA=cosB
D
2. 如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A. sinA的值越小,梯子越陡 B. cosA的值越小,梯子越陡
C. tanA的值越小,梯子越陡 D. 陡缓程度与∠A的函数值无关
B
3.在Rt△ABC中,∠C=90°,sinA= ,则tanB的值为_________.
5
12
4.如图,在Rt△ABC中,∠C=90°,cosA= ,
求sinA、tanA的值.
A
B
C
设AC=15k,则AB=17k
5.某商场为方便消费者购物,准备将原来的阶梯式
自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动
扶梯AB长为10m,坡角∠ABD为30°;改造后的斜坡式自动扶梯
的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度,
(结果精确到0.lm).
温馨提示:sin15°≈0.26,cosl5°≈0.97,tan15°≈0.27)
解:在Rt△ABD中,∠ABD=30°,AB=10m,
∴AD=ABsin∠ABD=10×sin30°=5,
在Rt△ACD中,
∠ACD=15°, sin∠ACD=
AC
AD
∴AC= = ≈ ≈19.2m
sin∠ACD
AD
sin15°
5
0.26
5
答:改造后的斜坡式自动扶梯AC的长度约为19.2米.
6.如图,在正方形ABCD中,M是AD的中点,BE=3AE,求sin∠ECM.
解:设正方形ABCD的边长为4x,∵M是AD的中点,BE=3AE,
∴AM=DM=2x,AE=x,BE=3x.
由勾股定理可知,
A
M
E
D
B
C
∴EM2=AM2+AE2=(2x)2+x2=5x2
CM2=DM2+DC2=(2x)2+(4x)2=20x2
EC2=BC2+BE2=(4x)2+(3x)2=25x2
∴ EC2=EM2+CM2
由勾股定理逆定理可知,△EMC为直角三角形.
A
M
E
D
B
C
课堂总结
1.在Rt△ABC中
2.梯子的倾斜程度与sinA和cosA的关系:
sinA的值越大,梯子越陡;
cosA的值越小,梯子越陡.
sinA=
c
a
=
cosA=
c
b
=
sinA=cosB
A
B
C
∠A的对边
∠A的邻边
┌
斜边
a
c
b
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
