整式乘法(一)[上学期]
文档属性
| 名称 | 整式乘法(一)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 191.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-12-07 19:12:00 | ||
图片预览








文档简介
课件23张PPT。整式的乘法小测试题 计算:
(1) (103)5 (2) (-x2)7
(3) (-3xy2)3 (4) (ab)10
(5) m3(-m)6 (-m)5
(6) (x+y)2· (x+y)3
(7)
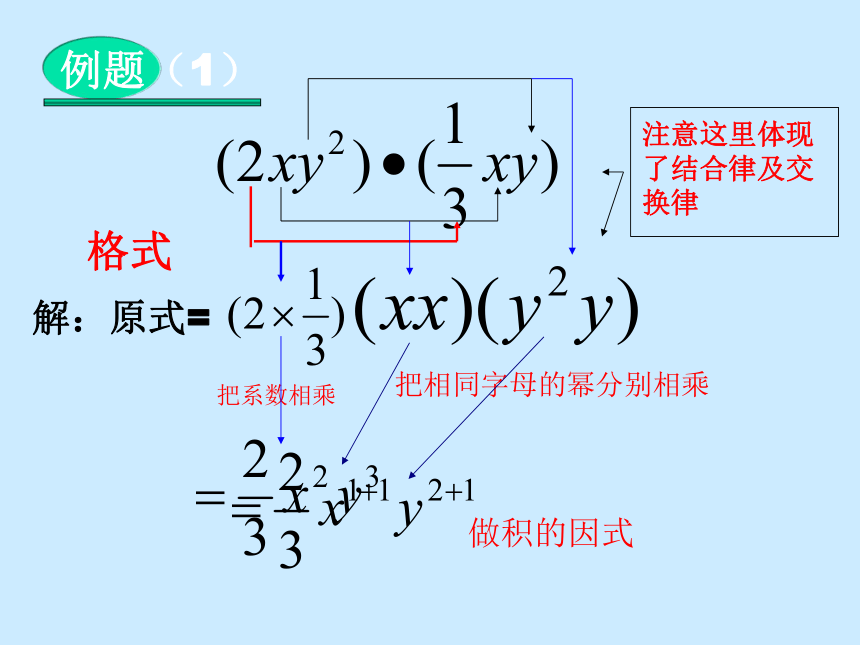
(8) (-2a3)2-(-4a2)3-[-(3a)2]3 (1)什么是单项式? (2)什么叫单项式的系数? (3)什么叫单项式的次数? 回忆1回忆2你知道这是什么吗?ab=ba你能说出结果吗?X2 x1=x3 这是前面才学过的同底数幂的乘法及积的乘方.问题:光的速度约为3×105千米/秒,太阳光照射到地球上需要的时间大约是5×102秒,你知道地球与太阳的距离约为多少千米吗?单项式乘以单项式法则:例题(1)格式解:原式=把系数相乘把相同字母的幂分别相乘做积的因式把系数相乘作为积的因式解:原式=例题(2)例题 (3)解:原式科学记数法表示的数也是单项式可以了吗?科学记数法是有规定的。结论一定要化简下面的计算对不 对?如果不对,怎样改正?⑴⑷⑶⑵⑸正确赛一赛:计算以下各题:(1)6x2·3xy (2)(2ab2)·( -3ab ) (3)(mn)2 ·(-m2n) (4) (-5amb) · (-2b2) (5)(4×106)(8×102) (6)(-3ab)·(-a2c)·6ab2(1)=18x3y
(2)=-6a2b3
(3)=-m4n3
(4)= 10am b3
(5)3.2×109
(6) 18a4b3c现在公布答案 如下图,学校有一块长为a米,宽为b米的矩
形操场,现在要割出一块边长分别为2c、b米的矩形
场地作篮球场,试用不同的方法表示余下的场地的
面积。从不同的表示方法中,你能得到什么结论?ba2c(1)s=b(a–2c)(2)s=ba–b?2c由(1)、 (2)可知b (a–2c) =ba–b?2c
b合作探究: 设长方形长为(a+b+c),宽为m,则面积为 这个长方形可分割为宽为m,长分别为a,b,c的三个小长方形,则它们的面积之和为ma+mb+mc. ∴ m(a+b+c)=ma+mb+mcm(a+b+c) =ma+mb+mc
m(a+b+c);
单项式与多项式相乘法则 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。即:m(a+b+c)=ma+mb+mc这里的m、a、b、c都是单项式计算:
(1)(- 2a) ? (2a 2 - 3a + 1)= (- 2a) ? 2a 2 +(- 2a) ?( - 3a)+(- 2a) ? 1= - 4a3+6a2 - 2a(乘法分配律)(单项式乘法)例4
(2) (- 4x) (2x2+3x-1)解:原式=(- 4x) ?2x2+(- 4x)?3x+(- 4x)?(-1) = - 8x3- 12x2+4x单项式与多项式相乘时,分两个阶段:①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算。 (3) ab ( ab2 - 2ab)解:原式= a2b3– a2b2几点注意:1.单项式乘多项式的结果仍是多项式,积的
项数与原多项式的项数相同。2.在单项式乘法运算中要注意系数的符号。 3.不要出现漏乘现象,运算要有顺序。试一试:(2)(-4x) ·(2x2+3x-1)
(3)(x-3y)(-6x)
(4)5x·(2x2-3x+4)
(5)(3m2y-xy2)·3xy
(6)5ab·(2a-b+0.2)解:原式= - a3b - 2a2b 2 - 5a3b+5a2b2= - 6a3b+3a2b2例5 化简:
-2a2?( ab+b2)- 5a(a2b - ab2)挑战自我:化简:x(x2–1)+2x2(x+1)–3x(2x-5)=x3–x+2x3+2x2–6x2+15x=3x3–4x2+14x求值:
yn(yn + 9y - 12) – 3(3yn+1 - 4yn),
其中y= - 3,n=2.解: yn(yn + 9y - 12) – 3(3yn+1 - 4yn)= y 2n+ 9yn+1- 12 yn– 9yn+1 +12 yn= y 2n当y= - 3,n=2时,原式=(- 3)4=81 求值问题,方法不是惟一
的,可以直接把字母的值代入
原式,但计算繁琐易出错,应
先化简,再代入求值,就显得
非常简捷。
(1) (103)5 (2) (-x2)7
(3) (-3xy2)3 (4) (ab)10
(5) m3(-m)6 (-m)5
(6) (x+y)2· (x+y)3
(7)
(8) (-2a3)2-(-4a2)3-[-(3a)2]3 (1)什么是单项式? (2)什么叫单项式的系数? (3)什么叫单项式的次数? 回忆1回忆2你知道这是什么吗?ab=ba你能说出结果吗?X2 x1=x3 这是前面才学过的同底数幂的乘法及积的乘方.问题:光的速度约为3×105千米/秒,太阳光照射到地球上需要的时间大约是5×102秒,你知道地球与太阳的距离约为多少千米吗?单项式乘以单项式法则:例题(1)格式解:原式=把系数相乘把相同字母的幂分别相乘做积的因式把系数相乘作为积的因式解:原式=例题(2)例题 (3)解:原式科学记数法表示的数也是单项式可以了吗?科学记数法是有规定的。结论一定要化简下面的计算对不 对?如果不对,怎样改正?⑴⑷⑶⑵⑸正确赛一赛:计算以下各题:(1)6x2·3xy (2)(2ab2)·( -3ab ) (3)(mn)2 ·(-m2n) (4) (-5amb) · (-2b2) (5)(4×106)(8×102) (6)(-3ab)·(-a2c)·6ab2(1)=18x3y
(2)=-6a2b3
(3)=-m4n3
(4)= 10am b3
(5)3.2×109
(6) 18a4b3c现在公布答案 如下图,学校有一块长为a米,宽为b米的矩
形操场,现在要割出一块边长分别为2c、b米的矩形
场地作篮球场,试用不同的方法表示余下的场地的
面积。从不同的表示方法中,你能得到什么结论?ba2c(1)s=b(a–2c)(2)s=ba–b?2c由(1)、 (2)可知b (a–2c) =ba–b?2c
b合作探究: 设长方形长为(a+b+c),宽为m,则面积为 这个长方形可分割为宽为m,长分别为a,b,c的三个小长方形,则它们的面积之和为ma+mb+mc. ∴ m(a+b+c)=ma+mb+mcm(a+b+c) =ma+mb+mc
m(a+b+c);
单项式与多项式相乘法则 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。即:m(a+b+c)=ma+mb+mc这里的m、a、b、c都是单项式计算:
(1)(- 2a) ? (2a 2 - 3a + 1)= (- 2a) ? 2a 2 +(- 2a) ?( - 3a)+(- 2a) ? 1= - 4a3+6a2 - 2a(乘法分配律)(单项式乘法)例4
(2) (- 4x) (2x2+3x-1)解:原式=(- 4x) ?2x2+(- 4x)?3x+(- 4x)?(-1) = - 8x3- 12x2+4x单项式与多项式相乘时,分两个阶段:①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算。 (3) ab ( ab2 - 2ab)解:原式= a2b3– a2b2几点注意:1.单项式乘多项式的结果仍是多项式,积的
项数与原多项式的项数相同。2.在单项式乘法运算中要注意系数的符号。 3.不要出现漏乘现象,运算要有顺序。试一试:(2)(-4x) ·(2x2+3x-1)
(3)(x-3y)(-6x)
(4)5x·(2x2-3x+4)
(5)(3m2y-xy2)·3xy
(6)5ab·(2a-b+0.2)解:原式= - a3b - 2a2b 2 - 5a3b+5a2b2= - 6a3b+3a2b2例5 化简:
-2a2?( ab+b2)- 5a(a2b - ab2)挑战自我:化简:x(x2–1)+2x2(x+1)–3x(2x-5)=x3–x+2x3+2x2–6x2+15x=3x3–4x2+14x求值:
yn(yn + 9y - 12) – 3(3yn+1 - 4yn),
其中y= - 3,n=2.解: yn(yn + 9y - 12) – 3(3yn+1 - 4yn)= y 2n+ 9yn+1- 12 yn– 9yn+1 +12 yn= y 2n当y= - 3,n=2时,原式=(- 3)4=81 求值问题,方法不是惟一
的,可以直接把字母的值代入
原式,但计算繁琐易出错,应
先化简,再代入求值,就显得
非常简捷。
