11.2.2三角形的外角 课件(31张PPT)
文档属性
| 名称 | 11.2.2三角形的外角 课件(31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 19:57:53 | ||
图片预览





文档简介
(共31张PPT)
11.2.2三角形的外角
人教版八年级上册
教学目标
1.理解并掌握三角形的外角的概念.
2.能够在能够复杂图形中找出外角.(难点)
3.掌握三角形的一个外角等于与它不相邻的两个内角的和及三角形的内角和.(重点)
4.会利用三角形的外角性质解决问题.
新知导入
1.在△ABC中,∠A=80°, ∠B=52°,则∠C= .
3.什么是三角形的内角?其内角和等于多少?
48 °
三角形相邻两边组成的角叫作三角形的内角,
它们的和是180 °.
2.如图,在△ABC中, ∠A=70°, ∠B=60°,则∠ACB= ,∠ACD= .
A
B
C
D
50 °
130°
新知讲解
B
D
C
A
O
●
40 °
70 °
?
●
●
●
问题:发现懒羊羊独自在O处游玩后,灰太狼打算用迂回的方式,先从A前进到C处,然后再折回到B处截住懒羊羊返回羊村的去路,红太狼则直接在A处拦截懒羊羊,已知∠BAC=40° , ∠ABC=70°.灰太狼从C处要转多少度角才能直达B处?
新知讲解
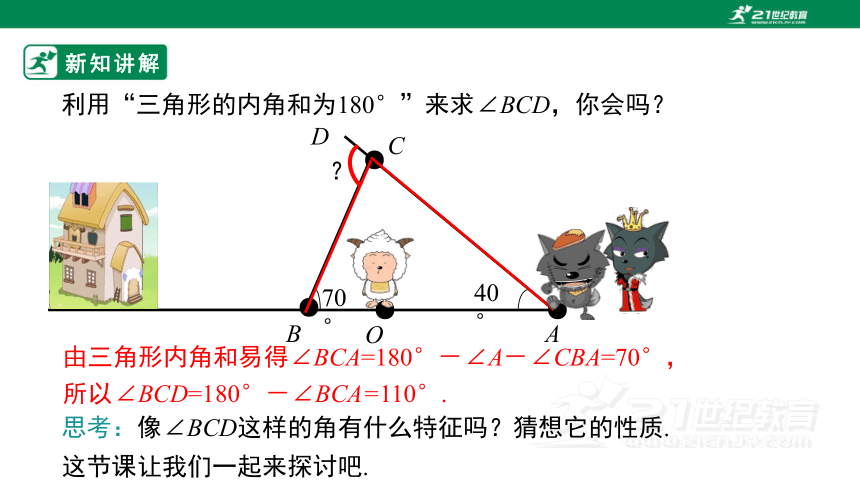
利用“三角形的内角和为180°”来求∠BCD,你会吗?
思考:像∠BCD这样的角有什么特征吗?猜想它的性质.
这节课让我们一起来探讨吧.
B
D
C
A
O
●
40 °
70 °
?
●
●
●
由三角形内角和易得∠BCA=180°-∠A-∠CBA=70°,
所以∠BCD=180°-∠BCA=110°.
新知讲解
三角形的外角的概念
一
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACD是△ABC的一个外角
C
B
A
D
新知讲解
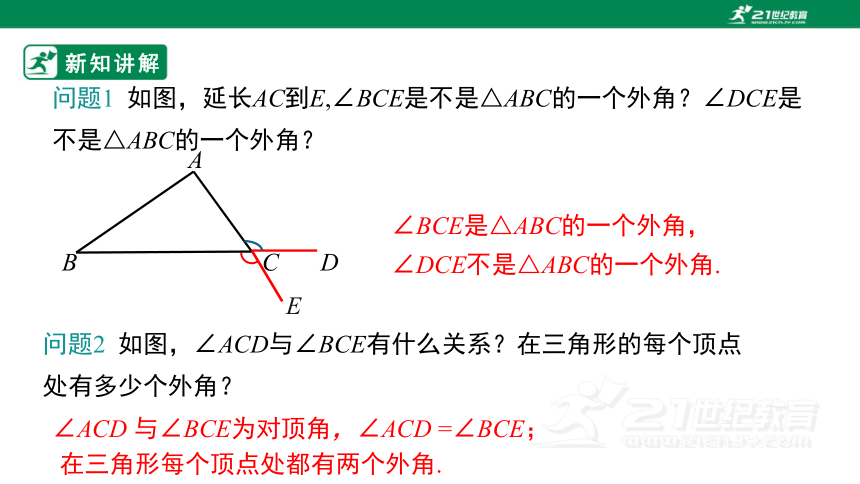
问题1 如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
C
B
A
D
∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
问题2 如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
新知讲解
A
B
C
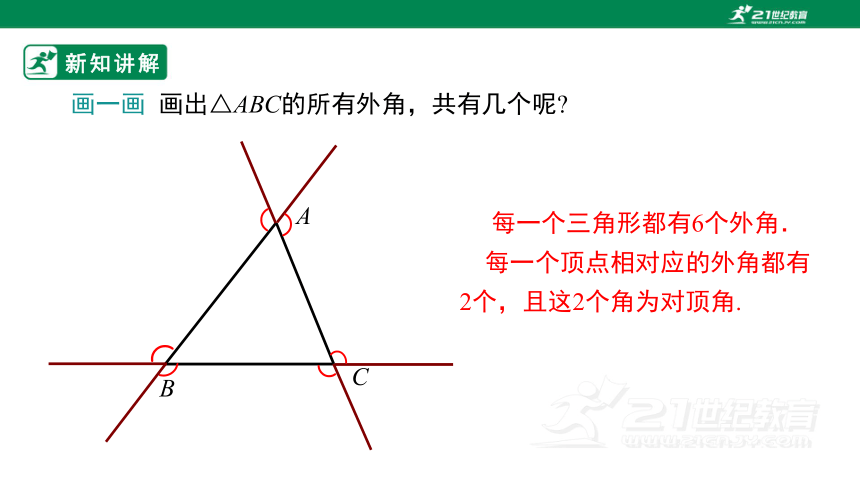
画一画 画出△ABC的所有外角,共有几个呢
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,且这2个角为对顶角.
新知讲解
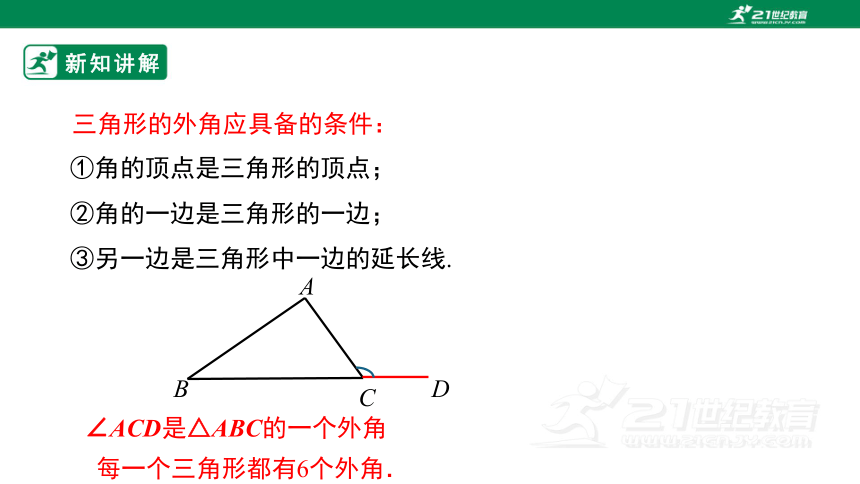
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
C
B
A
D
每一个三角形都有6个外角.
强化练习
F
A
B
C
D
E
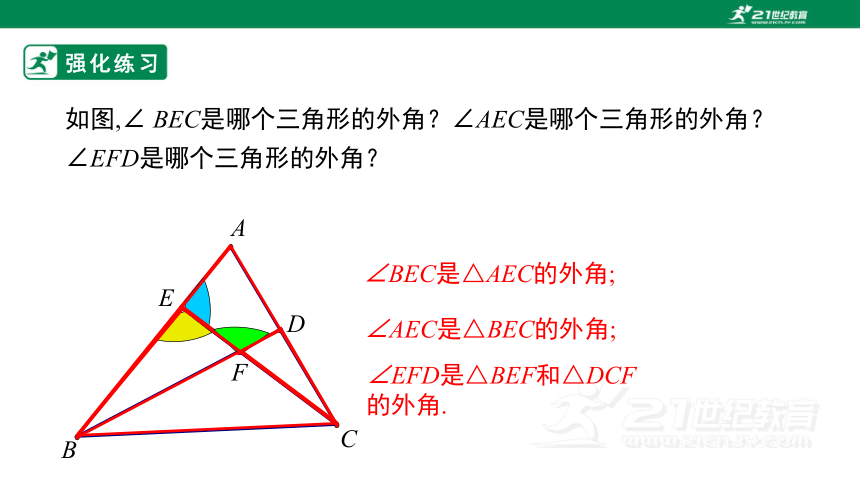
如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
新知讲解
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
三角形的外角的性质
二
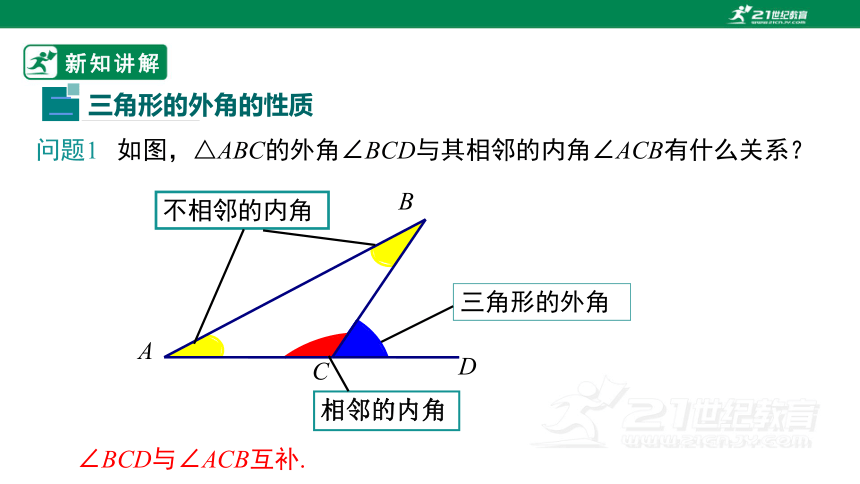
问题1 如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?
∠BCD与∠ACB互补.
新知讲解
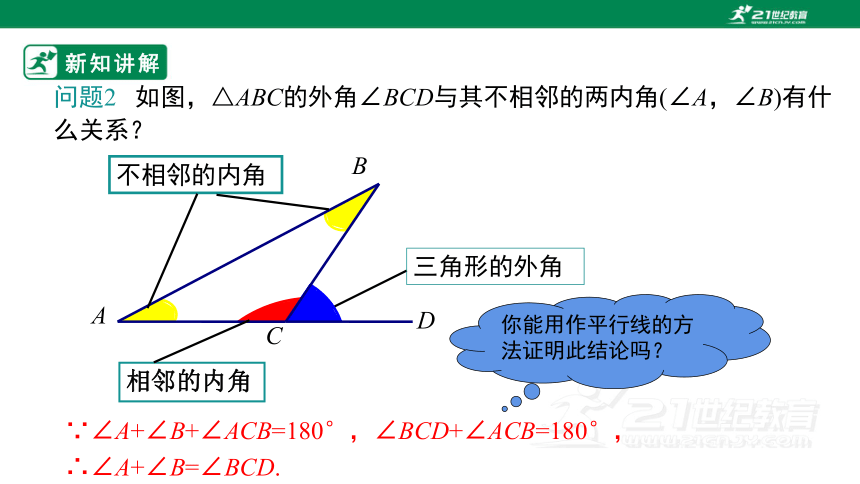
问题2 如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
你能用作平行线的方法证明此结论吗?
新知讲解
D
A
B
C
1
2
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
验证结论
问题3
新知讲解
三角形内角和定理的推论
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
应用格式:
∵ ∠ACD是△ABC的一个外角
∴ ∠ACD= ∠A+ ∠B.
知识要点
强化练习
练一练:说出下列图形中∠1和∠2的度数:
A
B
C
D
(
(
(
80 °
60 °
(
2
1
(1)
A
B
C
(
(
(
(
2
1
50 °
32 °
(2)
∠1=40 °, ∠2=140 °
∠1=18 °, ∠2=130 °
典例讲解
例1 如图,∠A=42°,∠ABD=28°,∠ACE=18°,
求∠BFC的度数.
F
A
C
D
E
B
典例讲解
例2 如图,P为△ABC内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°,求∠A的度数.
解析:延长BP交AC于E或连接AP并延长,构造三角形的外角,再利用外角的性质即可求出∠A的度数.
E
典例讲解
【变式题】 (一题多解)如图,∠A=51°,∠B=20°,
∠C=30°,求∠BDC的度数.
A
B
C
D
(
(
(
51 °
20 °
30 °
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
典例讲解
A
B
C
D
(
(
20 °
30 °
解法一:连接AD并延长于点E.
E
)
)
1
2
)
3
)
4
典例讲解
A
B
C
D
(
(
(
51 °
20 °
30 °
E
)
1
解法二:延长BD交AC于点E.
解法三:连接延长CD交AB于点F(解题过程同解法二).
)
2
F
解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
总结
强化练习
如图 ,试比较∠2 、∠1的大小;
如图 ,试比较∠3 、∠2、 ∠1的大小.
图
图
三角形的外角大于与它不相邻的内角.
典例讲解
三角形的外角和
三
例3 如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
你还有其他解法吗?
典例讲解
解法三:过A作AM平行于BC,
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠BAM,
所以 ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAM=360°
M
∠2+ ∠ 3= ∠ 4+∠BAM,
结论:三角形的外角和等于360°.
思考 你能总结出三角形的外角和的数量关系吗?
D
E
F
课堂小结
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360 °
强化练习
1.判断下列命题的对错.
(1)三角形的外角和是指三角形的所有外角的和. ( )
(2)三角形的外角和等于它的内角和的2倍. ( )
(3)三角形的一个外角等于两个内角的和. ( )
(4)三角形的一个外角等于与它不相邻的两个内角的和.( )
(5)三角形的一个外角大于任何一个内角. ( )
(6)三角形的一个内角小于任何一个与它不相邻的外角.( )
强化练习
2.如图,AB//CD,∠A=37°, ∠C=63°,那么∠F
等于 ( )
F
A
B
E
C
D
A.26°
B.63°
C.37°
D.60°
A
强化练习
3.(1)如图,∠BDC是________
的外角,也是 的外角;
(2)若∠B=45 °, ∠BAE=36 °,
∠BCE=20 °,试求∠AEC的度数.
A
B
C
D
E
△ADE
△ADC
答案:∠AEC=1100
强化练习
4 .如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求:
(1)∠B 的度数;(2)∠C的度数.
A
B
C
D
解:(1)∵∠ADC是△ABD的一个外角,
∴∠ADC=∠B+∠BAD,
又∵∠ADC=80°,∠B=∠BAD,
∴∠B=∠ADC=×80°=40°;
(2)在△ABC 中,
∵∠BAC+∠B+∠C=180°,
∴∠C=180°-∠B-∠BAC=180°-40°-70°=70°.
强化练习
A
B
C
D
E
1
2
F
G
5.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
答案:∠A+ ∠B+ ∠C+ ∠D+ ∠E=1800
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.2.2三角形的外角
人教版八年级上册
教学目标
1.理解并掌握三角形的外角的概念.
2.能够在能够复杂图形中找出外角.(难点)
3.掌握三角形的一个外角等于与它不相邻的两个内角的和及三角形的内角和.(重点)
4.会利用三角形的外角性质解决问题.
新知导入
1.在△ABC中,∠A=80°, ∠B=52°,则∠C= .
3.什么是三角形的内角?其内角和等于多少?
48 °
三角形相邻两边组成的角叫作三角形的内角,
它们的和是180 °.
2.如图,在△ABC中, ∠A=70°, ∠B=60°,则∠ACB= ,∠ACD= .
A
B
C
D
50 °
130°
新知讲解
B
D
C
A
O
●
40 °
70 °
?
●
●
●
问题:发现懒羊羊独自在O处游玩后,灰太狼打算用迂回的方式,先从A前进到C处,然后再折回到B处截住懒羊羊返回羊村的去路,红太狼则直接在A处拦截懒羊羊,已知∠BAC=40° , ∠ABC=70°.灰太狼从C处要转多少度角才能直达B处?
新知讲解
利用“三角形的内角和为180°”来求∠BCD,你会吗?
思考:像∠BCD这样的角有什么特征吗?猜想它的性质.
这节课让我们一起来探讨吧.
B
D
C
A
O
●
40 °
70 °
?
●
●
●
由三角形内角和易得∠BCA=180°-∠A-∠CBA=70°,
所以∠BCD=180°-∠BCA=110°.
新知讲解
三角形的外角的概念
一
定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
∠ACD是△ABC的一个外角
C
B
A
D
新知讲解
问题1 如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
C
B
A
D
∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
问题2 如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
新知讲解
A
B
C
画一画 画出△ABC的所有外角,共有几个呢
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,且这2个角为对顶角.
新知讲解
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
C
B
A
D
每一个三角形都有6个外角.
强化练习
F
A
B
C
D
E
如图,∠ BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
新知讲解
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
三角形的外角的性质
二
问题1 如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?
∠BCD与∠ACB互补.
新知讲解
问题2 如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
你能用作平行线的方法证明此结论吗?
新知讲解
D
A
B
C
1
2
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
验证结论
问题3
新知讲解
三角形内角和定理的推论
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
应用格式:
∵ ∠ACD是△ABC的一个外角
∴ ∠ACD= ∠A+ ∠B.
知识要点
强化练习
练一练:说出下列图形中∠1和∠2的度数:
A
B
C
D
(
(
(
80 °
60 °
(
2
1
(1)
A
B
C
(
(
(
(
2
1
50 °
32 °
(2)
∠1=40 °, ∠2=140 °
∠1=18 °, ∠2=130 °
典例讲解
例1 如图,∠A=42°,∠ABD=28°,∠ACE=18°,
求∠BFC的度数.
F
A
C
D
E
B
典例讲解
例2 如图,P为△ABC内一点,∠BPC=150°,∠ABP=20°,∠ACP=30°,求∠A的度数.
解析:延长BP交AC于E或连接AP并延长,构造三角形的外角,再利用外角的性质即可求出∠A的度数.
E
典例讲解
【变式题】 (一题多解)如图,∠A=51°,∠B=20°,
∠C=30°,求∠BDC的度数.
A
B
C
D
(
(
(
51 °
20 °
30 °
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
典例讲解
A
B
C
D
(
(
20 °
30 °
解法一:连接AD并延长于点E.
E
)
)
1
2
)
3
)
4
典例讲解
A
B
C
D
(
(
(
51 °
20 °
30 °
E
)
1
解法二:延长BD交AC于点E.
解法三:连接延长CD交AB于点F(解题过程同解法二).
)
2
F
解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
总结
强化练习
如图 ,试比较∠2 、∠1的大小;
如图 ,试比较∠3 、∠2、 ∠1的大小.
图
图
三角形的外角大于与它不相邻的内角.
典例讲解
三角形的外角和
三
例3 如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
你还有其他解法吗?
典例讲解
解法三:过A作AM平行于BC,
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠BAM,
所以 ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAM=360°
M
∠2+ ∠ 3= ∠ 4+∠BAM,
结论:三角形的外角和等于360°.
思考 你能总结出三角形的外角和的数量关系吗?
D
E
F
课堂小结
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360 °
强化练习
1.判断下列命题的对错.
(1)三角形的外角和是指三角形的所有外角的和. ( )
(2)三角形的外角和等于它的内角和的2倍. ( )
(3)三角形的一个外角等于两个内角的和. ( )
(4)三角形的一个外角等于与它不相邻的两个内角的和.( )
(5)三角形的一个外角大于任何一个内角. ( )
(6)三角形的一个内角小于任何一个与它不相邻的外角.( )
强化练习
2.如图,AB//CD,∠A=37°, ∠C=63°,那么∠F
等于 ( )
F
A
B
E
C
D
A.26°
B.63°
C.37°
D.60°
A
强化练习
3.(1)如图,∠BDC是________
的外角,也是 的外角;
(2)若∠B=45 °, ∠BAE=36 °,
∠BCE=20 °,试求∠AEC的度数.
A
B
C
D
E
△ADE
△ADC
答案:∠AEC=1100
强化练习
4 .如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求:
(1)∠B 的度数;(2)∠C的度数.
A
B
C
D
解:(1)∵∠ADC是△ABD的一个外角,
∴∠ADC=∠B+∠BAD,
又∵∠ADC=80°,∠B=∠BAD,
∴∠B=∠ADC=×80°=40°;
(2)在△ABC 中,
∵∠BAC+∠B+∠C=180°,
∴∠C=180°-∠B-∠BAC=180°-40°-70°=70°.
强化练习
A
B
C
D
E
1
2
F
G
5.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
答案:∠A+ ∠B+ ∠C+ ∠D+ ∠E=1800
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
