人教A版(2019)高中数学选择性必修第三册 两个计数原理与排列、组合课件(共25张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 两个计数原理与排列、组合课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 804.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
习题课 两个计数原理与排列、组合
1.进一步理解和掌握分类加法计数原理和分步乘法计数原理.
2.进一步深化排列与组合的概念.
3.能综合运用排列、组合解决计数问题.
题型探究
达标检测
学习目标
类型一 两个计数原理的应用
角度1 “类中有步”的计数问题
例1 电视台在某节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙信箱中有20封,现由主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有_____种不同的选择.
解析答案
反思与感悟
题型探究 重点难点 个个击破
解析 在甲箱或乙箱中抽取幸运之星,决定了后边选幸运伙伴是不同的,故要分两类分别计算:(1)幸运之星在甲箱中抽,先确定幸运之星,再在两箱中各确定一名幸运伙伴有30×29×20=17 400(种)结果;
(2)幸运之星在乙箱中抽,同理有20×19×30=11 400(种)结果.
因此共有不同结果17 400+11 400=28 800(种).
答案 28 800
反思与感悟
反思与感悟
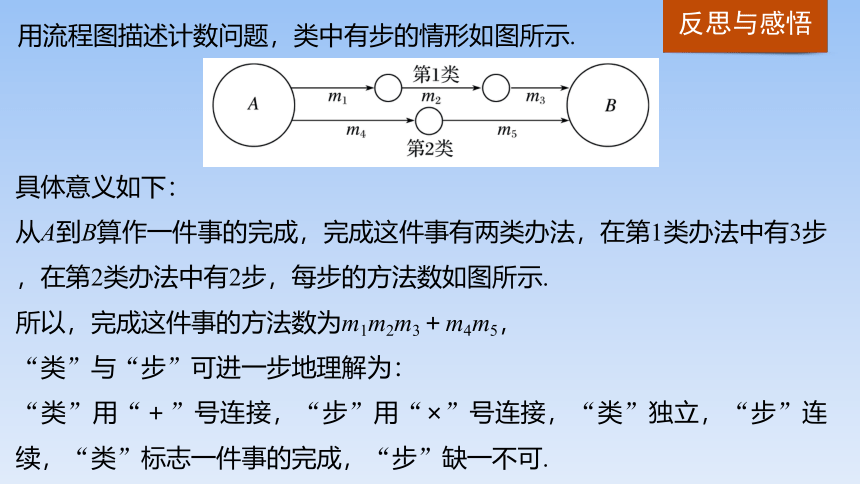
用流程图描述计数问题,类中有步的情形如图所示.
具体意义如下:
从A到B算作一件事的完成,完成这件事有两类办法,在第1类办法中有3步,在第2类办法中有2步,每步的方法数如图所示.
所以,完成这件事的方法数为m1m2m3+m4m5,
“类”与“步”可进一步地理解为:
“类”用“+”号连接,“步”用“×”号连接,“类”独立,“步”连续,“类”标志一件事的完成,“步”缺一不可.
解析答案
跟踪训练1 现有4种不同颜色,要对如图所示的四个部分进行着色,要求有公共边界的两部分不能用同一种颜色,则不同的着色方法共有( )
A.24种 B.30种 C.36种 D.48种
解析 将原图从上而下的4个区域标为1,2,3,4.
因为1,2,3之间不能同色,1与4可以同色,
因此,要分类讨论1,4同色与不同色这两种情况.
故不同的着色方法种数为4×3×2+4×3×2×1=48.
故选D.
D
解析答案
角度2 “步中有类”的计数问题
例2 有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测一人,则不同的安排方式共有________种(用数字作答).
反思与感悟
解析 上午总测试方法有4×3×2×1=24(种);
我们以A、B、C、D、E依次代表五个测试项目.
若上午测试E的同学下午测试D,则上午测试A的同学下午只能测试B、C,确定上午测试A的同学后其余两位同学上、下午的测试方法共有2种;
若上午测试E的同学下午测试A、B、C之一,则上午测试A、B、C中任何一个的同学下午都可以测试D,安排完这位同学后其余两位同学的测试方式就确定了,故共有3×3=9(种)测试方法,
即下午的测试方法共有11种,
根据分步乘法计数原理,总的测试方法共有24×11=264(种).
答案 264
反思与感悟
用流程图描述计数问题,步中有类的情形如图所示:
反思与感悟
从计数的角度看,由A到D算作完成一件事,可简单地记为A→D.
完成A→D这件事,需要经历三步,即A→B,B→C,C→D.其中B→C这步又分为三类,这就是步中有类.
其中mi(i=1,2,3,4,5)表示相应步的方法数.
完成A→D这件事的方法数为m1(m2+m3+m4)m5.
以上给出了处理步中有类问题的一般方法.
解析答案
跟踪训练2 如图所示,使电路接通,开关不同的开闭方式共有( )
A.11 B.12
C.20 D.21
解析 根据题意,设5个开关依次为1、2、3、4、5,
若电路接通,则开关1、2与3、4、5中至少有1个接通,
对于开关1、2,共有2×2=4(种)情况,
其中全部断开的有1种情况,
则其至少有1个接通的有4-1=3(种)情况,
对于开关3、4、5,共有2×2×2=8(种)情况,
其中全部断开的有1种情况,
则其至少有1个接通的8-1=7(种)情况,
则电路接通的情况有3×7=21(种).故选D.
答案 D
解析答案
类型二 排列与组合的综合应用
角度1 不同元素的排列、组合问题
例3 有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行.如果取出的4张卡片所标的数字之和等于10,则不同的排法共有多少种?
反思与感悟
解 分三类:
第1类,当取出的4张卡片分别标有数字1,2,3,4时,
第2类,当取出的4张卡片分别标有数字1,1,4,4时,
第3类,当取出的4张卡片分别标有数字2,2,3,3时,
反思与感悟
1.解排列、组合综合问题的一般思路是“先选后排”,也就是先把符合题意的元素都选出来,再对元素或位置进行排列.
2.解排列、组合综合问题时要注意以下几点:
(1)元素是否有序是区分排列与组合的基本方法,无序的问题是组合问题,有序的问题是排列问题.
(2)对于有多个限制条件的复杂问题,应认真分析每个限制条件,然后再考虑是分类还是分步,这是处理排列、组合综合问题的一般方法.
反思与感悟
解析答案
跟踪训练3 从1,3,5,7,9中任取3个数字,从0,2,4,6,8中任取2个数字,一共可以组成多少个没有重复数字的五位偶数?
解析答案
解 (1)五位数中不含数字0.
(2)五位数中含有数字0.
第2步,排顺序又可分为两小类:
∴符合条件的偶数个数为
解析答案
角度2 含有相同元素的排列、组合问题
例4 将10个优秀名额分配到一班、二班、三班3个班级中,若各班名额数不小于班级序号数,共有____种不同的分配方案.
解析 先拿3个优秀名额分配给二班1个,三班2个,这样原问题就转化为将7个优秀名额分配到3个班级中,每个班级中至少分配到1个.
15
反思与感悟
凡“相同小球放入不同盒中”的问题,即为“n个相同元素有序分成m组(每组的任务不同)”的问题,一般可用“隔板法”求解:
(1)当每组至少含一个元素时,其不同分组方式有 种,即将n个元素中间的n-1个空格中加入m-1个“隔板”.
(2)任意分组,可出现某些组含元素为0个的情况,其不同分组方式有
种,即将n个相同元素与m-1个相同“隔板”进行排序,在n+m-1个位置中选m-1个安排“隔板”.
反思与感悟
跟踪训练4 用2,3,4,5,6,7六个数字,可以组成有重复数字的三位数的个数为_____.
解析 用间接法:六个数字能构成的三位数共6×6×6=216(个),
故所求的三位数的个数为216-120=96.
96
解析答案
返回
达标检测
1.某电话局的电话号码为168 ,若后面的五位数字是由6或8组成的,则这样的电话号码一共有( )
A.20个 B.25个
C.32个 D.48个
1
2
3
4
C
答案
* * * * *
解析答案
2.现安排甲、乙、丙、丁、戊5名同学参加某项服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加.甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是( )
A.152 B.126 C.90 D.54
解析 按从事司机工作的人数进行分类:
∴不同安排方案的种数是108+18=126.
B
1
2
3
4
解析答案
3.某电视台连续播放5个广告,其中有3个不同的商业广告和2个不同的公益宣传广告,要求最后播放的必须是公益宣传广告,且2个公益宣传广告不能连续播放,则不同的播放方式有___种.
解析 先安排后2个,再安排前3个,
36
1
2
3
4
解析答案
4.将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里球的个数不小于该盒子的编号,则不同的放球方法有___种.
∴共有10种不同的放球方法.
10
1
2
3
4
返回
规律与方法
1.分类加法计数原理与分步乘法计数原理是两个最基本、也是最重要的原理,是解答排列、组合问题,尤其是较复杂的排列、组合问题的基础.
2.解排列、组合综合题一般是先选元素、后排元素,或充分利用元素的性质进行分类、分步,再利用两个基本计数原理作最后处理.
3.对于较难直接解决的问题则可用间接法,但应做到不重不漏.
4.对于分配问题,解题的关键是要搞清楚事件是否与顺序有关,对于平均分组问题更要注意顺序,避免计数的重复或遗漏.
习题课 两个计数原理与排列、组合
1.进一步理解和掌握分类加法计数原理和分步乘法计数原理.
2.进一步深化排列与组合的概念.
3.能综合运用排列、组合解决计数问题.
题型探究
达标检测
学习目标
类型一 两个计数原理的应用
角度1 “类中有步”的计数问题
例1 电视台在某节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙信箱中有20封,现由主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有_____种不同的选择.
解析答案
反思与感悟
题型探究 重点难点 个个击破
解析 在甲箱或乙箱中抽取幸运之星,决定了后边选幸运伙伴是不同的,故要分两类分别计算:(1)幸运之星在甲箱中抽,先确定幸运之星,再在两箱中各确定一名幸运伙伴有30×29×20=17 400(种)结果;
(2)幸运之星在乙箱中抽,同理有20×19×30=11 400(种)结果.
因此共有不同结果17 400+11 400=28 800(种).
答案 28 800
反思与感悟
反思与感悟
用流程图描述计数问题,类中有步的情形如图所示.
具体意义如下:
从A到B算作一件事的完成,完成这件事有两类办法,在第1类办法中有3步,在第2类办法中有2步,每步的方法数如图所示.
所以,完成这件事的方法数为m1m2m3+m4m5,
“类”与“步”可进一步地理解为:
“类”用“+”号连接,“步”用“×”号连接,“类”独立,“步”连续,“类”标志一件事的完成,“步”缺一不可.
解析答案
跟踪训练1 现有4种不同颜色,要对如图所示的四个部分进行着色,要求有公共边界的两部分不能用同一种颜色,则不同的着色方法共有( )
A.24种 B.30种 C.36种 D.48种
解析 将原图从上而下的4个区域标为1,2,3,4.
因为1,2,3之间不能同色,1与4可以同色,
因此,要分类讨论1,4同色与不同色这两种情况.
故不同的着色方法种数为4×3×2+4×3×2×1=48.
故选D.
D
解析答案
角度2 “步中有类”的计数问题
例2 有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测一人,则不同的安排方式共有________种(用数字作答).
反思与感悟
解析 上午总测试方法有4×3×2×1=24(种);
我们以A、B、C、D、E依次代表五个测试项目.
若上午测试E的同学下午测试D,则上午测试A的同学下午只能测试B、C,确定上午测试A的同学后其余两位同学上、下午的测试方法共有2种;
若上午测试E的同学下午测试A、B、C之一,则上午测试A、B、C中任何一个的同学下午都可以测试D,安排完这位同学后其余两位同学的测试方式就确定了,故共有3×3=9(种)测试方法,
即下午的测试方法共有11种,
根据分步乘法计数原理,总的测试方法共有24×11=264(种).
答案 264
反思与感悟
用流程图描述计数问题,步中有类的情形如图所示:
反思与感悟
从计数的角度看,由A到D算作完成一件事,可简单地记为A→D.
完成A→D这件事,需要经历三步,即A→B,B→C,C→D.其中B→C这步又分为三类,这就是步中有类.
其中mi(i=1,2,3,4,5)表示相应步的方法数.
完成A→D这件事的方法数为m1(m2+m3+m4)m5.
以上给出了处理步中有类问题的一般方法.
解析答案
跟踪训练2 如图所示,使电路接通,开关不同的开闭方式共有( )
A.11 B.12
C.20 D.21
解析 根据题意,设5个开关依次为1、2、3、4、5,
若电路接通,则开关1、2与3、4、5中至少有1个接通,
对于开关1、2,共有2×2=4(种)情况,
其中全部断开的有1种情况,
则其至少有1个接通的有4-1=3(种)情况,
对于开关3、4、5,共有2×2×2=8(种)情况,
其中全部断开的有1种情况,
则其至少有1个接通的8-1=7(种)情况,
则电路接通的情况有3×7=21(种).故选D.
答案 D
解析答案
类型二 排列与组合的综合应用
角度1 不同元素的排列、组合问题
例3 有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行.如果取出的4张卡片所标的数字之和等于10,则不同的排法共有多少种?
反思与感悟
解 分三类:
第1类,当取出的4张卡片分别标有数字1,2,3,4时,
第2类,当取出的4张卡片分别标有数字1,1,4,4时,
第3类,当取出的4张卡片分别标有数字2,2,3,3时,
反思与感悟
1.解排列、组合综合问题的一般思路是“先选后排”,也就是先把符合题意的元素都选出来,再对元素或位置进行排列.
2.解排列、组合综合问题时要注意以下几点:
(1)元素是否有序是区分排列与组合的基本方法,无序的问题是组合问题,有序的问题是排列问题.
(2)对于有多个限制条件的复杂问题,应认真分析每个限制条件,然后再考虑是分类还是分步,这是处理排列、组合综合问题的一般方法.
反思与感悟
解析答案
跟踪训练3 从1,3,5,7,9中任取3个数字,从0,2,4,6,8中任取2个数字,一共可以组成多少个没有重复数字的五位偶数?
解析答案
解 (1)五位数中不含数字0.
(2)五位数中含有数字0.
第2步,排顺序又可分为两小类:
∴符合条件的偶数个数为
解析答案
角度2 含有相同元素的排列、组合问题
例4 将10个优秀名额分配到一班、二班、三班3个班级中,若各班名额数不小于班级序号数,共有____种不同的分配方案.
解析 先拿3个优秀名额分配给二班1个,三班2个,这样原问题就转化为将7个优秀名额分配到3个班级中,每个班级中至少分配到1个.
15
反思与感悟
凡“相同小球放入不同盒中”的问题,即为“n个相同元素有序分成m组(每组的任务不同)”的问题,一般可用“隔板法”求解:
(1)当每组至少含一个元素时,其不同分组方式有 种,即将n个元素中间的n-1个空格中加入m-1个“隔板”.
(2)任意分组,可出现某些组含元素为0个的情况,其不同分组方式有
种,即将n个相同元素与m-1个相同“隔板”进行排序,在n+m-1个位置中选m-1个安排“隔板”.
反思与感悟
跟踪训练4 用2,3,4,5,6,7六个数字,可以组成有重复数字的三位数的个数为_____.
解析 用间接法:六个数字能构成的三位数共6×6×6=216(个),
故所求的三位数的个数为216-120=96.
96
解析答案
返回
达标检测
1.某电话局的电话号码为168 ,若后面的五位数字是由6或8组成的,则这样的电话号码一共有( )
A.20个 B.25个
C.32个 D.48个
1
2
3
4
C
答案
* * * * *
解析答案
2.现安排甲、乙、丙、丁、戊5名同学参加某项服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加.甲、乙不会开车但能从事其他三项工作,丙、丁、戊都能胜任四项工作,则不同安排方案的种数是( )
A.152 B.126 C.90 D.54
解析 按从事司机工作的人数进行分类:
∴不同安排方案的种数是108+18=126.
B
1
2
3
4
解析答案
3.某电视台连续播放5个广告,其中有3个不同的商业广告和2个不同的公益宣传广告,要求最后播放的必须是公益宣传广告,且2个公益宣传广告不能连续播放,则不同的播放方式有___种.
解析 先安排后2个,再安排前3个,
36
1
2
3
4
解析答案
4.将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里球的个数不小于该盒子的编号,则不同的放球方法有___种.
∴共有10种不同的放球方法.
10
1
2
3
4
返回
规律与方法
1.分类加法计数原理与分步乘法计数原理是两个最基本、也是最重要的原理,是解答排列、组合问题,尤其是较复杂的排列、组合问题的基础.
2.解排列、组合综合题一般是先选元素、后排元素,或充分利用元素的性质进行分类、分步,再利用两个基本计数原理作最后处理.
3.对于较难直接解决的问题则可用间接法,但应做到不重不漏.
4.对于分配问题,解题的关键是要搞清楚事件是否与顺序有关,对于平均分组问题更要注意顺序,避免计数的重复或遗漏.
