人教A版(2019)高中数学选择性必修第三册 《排列与排列数---习题课》名师课件(共25张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 《排列与排列数---习题课》名师课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 10:13:33 | ||
图片预览

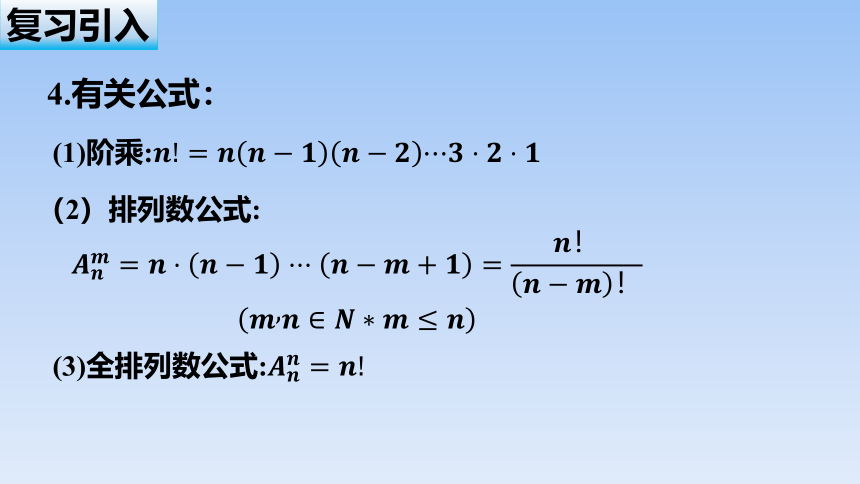







文档简介
(共25张PPT)
复习引入
1、排列:
一般地,从个不同中取出()个元素,按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
2、排列数:
从个不同的元素中取出()个元素的所有排列的个数,叫做从个不同的元素中取出个元素的排列数.用符号表示.
3、排列数:
个不同元素全部取出的一个排列,叫做个不同元素的一个全排列.
(3)全排列数公式:
4.有关公式:
(2)排列数公式:
复习引入
(1)阶乘:
人教A版同步教材名师课件
排列与排列数
---习题课
学习目标
学 习 目 标 核心素养
通过分析、比较,掌握解排列问题的基本方法 数学运算
启发学生提升提出问题、分析问题和创造性地解决问题的能力 逻辑推理
学习目标
学习目标:
1.排列数的简单应用.
2.解排列问题的基本方法(捆绑法、插空法等)的灵活应用.
学科核心素养:
1.通过渗透分类讨论的数学思想,发展学生的逻辑推理核心素养
2通过探究与活动,明白考虑问题要细致,说理要明确,发展学生的数学抽象与数学运算核心素养
3通过对生活中的排列问题研究的过程,体会数学的实际应用价值教学重点难点
例1、用0到9这10个数字,可以组成多少个没有重复数字的三位数?
法一:由于在没有重复数字的三位数中,百位上的数字不能是0,因此可以分两步完成排列.
第1步,排百位上的数字,可以从1到9这九个数字中任选1个,有种选法.
第2步:排十位和个位上的数字,可以从余下的9个数字中任选2个,有种选法;
由分步乘法计数原理,所求的三位数的个数为×=9×9×8=648.
典例讲解
解析
法二:符合条件的三位数可分成3类.
①每一位数字都不是0的三位数有个;
②个位数字是0的三位数有个;
③十位数字是0的三位数有个;
根据分类加法计数原理:符合条件的三位数的个数为648.
典例讲解
例1、用0到9这10个数字,可以组成多少个没有重复数字的三位数?
解析
法三:从0到9这10个数字中任取3个数字的排列数为,其中0在百位上的排列数是,它们的差就是用这10个数字组成的没有重复数字的三位数的个数,即所求的三位数的个数为=
典例讲解
例1、用0到9这10个数字,可以组成多少个没有重复数字的三位数?
解析
方法归纳
不同数字的无重复排列是排列问题中的一类典型问题.其常见的附加条件有:奇偶数、倍数关系、大小关系等,也可以有相邻问题、插空问题,也可以与数列等知识相联系等.解决这类问题的关键是搞清事件是什么,元素是什么,位置是什么,给出了什么样的附加条件,然后按特殊元素(位置)的性质分类(每一类的各种方法都能保证事件的完成),按事件发生的连续过程合理分步来解决.这类问题的隐含条件“ 0不能在首位”尤其不能忽略.
变式训练
1.用0,1,2,3,4,5这六个数字,可以组成多少个分别符合下列条件的无重复数字的四位数:
(1)奇数;
(2)偶数;
(3)大于3 125的数
(1)先排个位,再排首位,共有=144(个).
(2)以0结尾的四位偶数有个,以2或4结尾的四位偶数有个,则共有+ =156(个).
(3)要比3 125大,4,5作千位时有个,3作千位,2,4,5作百位时有个,3作千位,1作百位,4,5作十位时有个,所以共有(个).
解析
例2、3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(1)全体站成一排,男、女各站在一起;
(2)全体站成一排,男生必须站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,男、女各不相邻.
典例讲解
(1)男生必须站在一起是男生的全排列,有种排法;女生必须站在一起是女生的全排列,有种排法;全体男生、女生各视为一个元素,有种排法.由分步计数原理知,共有· · =288种排队方法.
(2)三个男生全排列有种方法,把所有男生视为一个元素,与4名女生组成5个元素全排列,有种排法.故有· =720种排队方法.
解析
例2、3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(1)全体站成一排,男、女各站在一起;
(2)全体站成一排,男生必须站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,男、女各不相邻.
典例讲解
(3)先安排女生,共有种排法;男生在4个女生隔成的五个空中安排,共有种排法,故共有· =1 440种排法.
(4)排好男生后让女生插空,共有· =144种排法.
解析
方法归纳
本题是“邻”与“不邻”类型的排列问题.
(1)某些元素要求不相邻时,可以先安排其他元素,再将这些不相邻元素插入空位,这种方法称为“插空法”,即“不相邻元素插空法”.
(2)对于某些元素“相邻”的排列问题,一般采用“捆绑法”,即先把相邻的若干个元素“捆绑”为一个大元素与其余元素全排列,然后再松绑,将这若干个元素内部全排列
变式训练
2.某次文艺晚会上共演出8个节目,其中2个唱歌、3个舞蹈、3个曲艺节目,求分别满足下列条件的节目编排方法有多少种?
(1)一个唱歌节目开头,另一个放在最后压台;
(2)2个唱歌节目互不相邻;
(3)2个唱歌节目相邻且3个舞蹈节目不相邻.
(1)先排唱歌节目有种排法,再排其他节目有种排法,所以共有· =1 440种排法.
(2)先排3个舞蹈节目和3个曲艺节目有种排法,再从其中7个空(包括两端)中选2个排唱歌节目,有种插入方法,所以共有· =30 240种排法.
(3)把2个相邻的唱歌节目看作一个元素,与3个曲艺节目排列共种排法,再将3个舞蹈节目插入,共有种插入方法,最后将2个唱歌节目互换位置,有种排法,故所求排法共有· · =2 880种排法.
解析
例3、某一天的课程表要排入政治、语文、数学、物理、体育、美术共六节课,如果第一节不排体育,最后一节不排数学,那么共有多少种不同课程表的排法?
典例讲解
法一:6门课总的排法是种,其中不符合要求的可分为:
体育排在第一节有种排法,如图中Ⅰ;
数学排在最后一节有种排法,如图中Ⅱ;
但这两种方法,都包括体育在第一节,数学排在最后一节,如图中Ⅲ,这种情况有种排法;
因此符合条件的排法应是:504(种).
解析
典例讲解
法二:根据要求,课程表安排可分为4种情况:
(1)体育、数学既不排在第一节也不排在最后一节,这种情况有· 种排法;
(2)数学排在第一节但体育不排在最后一节,有· 种排法;
(3)体育排在最后一节但数学不排在第一节,有· 种排法;
(4)数学排在第一节,体育排在最后一节,有种排法.
这四类排法并列,不重复也不遗漏,故总的排法有:
· + · + · + =504(种).
例3、某一天的课程表要排入政治、语文、数学、物理、体育、美术共六节课,如果第一节不排体育,最后一节不排数学,那么共有多少种不同课程表的排法?
解析
方法归纳
本题是属于“在”与“不在”问题,是排列问题中的常见类型,常用“元素分析法”“位置分析法”.当题目中有两个约束条件时,往往考虑一个约束条件的同时,还需要考虑另一个约束条件,这就要进行正确的分类,有时分的类较多,用直接法较麻烦,往往采用“间接法”.
变式训练
设,且成等差数列,则,即应是偶数.因此从1到20这20个数字中任选出三个数成等差数列,则第一个数与第三个数必同为偶数或同为奇数,而1到20这20个数字中有10个偶数和10个奇数.当第一个和第三个数选定后,中间数被唯一确定.因此,选法只有两类:
(1)第一、三个数都是偶数,有种选法;
(2)第一、三个数都是奇数,有种选法;
于是,选出3个数成等差数列的个数为+ =180(个).
3.从集合{1,2,3,…,20}中任选出3个不同的数,使这3个数成等差数列,这样的等差数列可以有多少个?
解析
1.对有约束条件的排列问题,应注意如下类型:
⑴某些元素不能在或必须排列在某一位置;
⑵某些元素要求连排(即必须相邻);
⑶某些元素要求分离(即不能相邻);
2.基本的解题方法:
(1)有特殊元素或特殊位置的排列问题,通常是先排特殊元素或特殊位置,称为优先处理特殊元素(位置)法(优先法);
特殊元素,特殊位置优先安排策略
素养提炼
素养提炼
(3)某些元素不相邻排列时,可以先排其他元素,再将这些不相邻元素插入空挡,这种方法称为“插空法”;
不相邻问题插空处理的策略
(2)某些元素要求必须相邻时,可以先将这些元素看作一个元素,与其他元素排列后,再考虑相邻元素的内部排列,这种方法称为“捆绑法”;
相邻问题捆绑处理的策略
当堂练习
1.六个停车位置,有3辆汽车需要停放,若要使三个空位连在一起,则停放的方法数为________.
把3个空位看作一个元素,与3辆汽车共有4个元素全排列,故停放的方法有=4×3×2×1=24种.
24
解析
2.分别求出符合下列要求的不同排法的种数.
(1)6名学生排3排,前排1人,中排2人,后排3人;
(2)6名学生排成一排,甲不在排头也不在排尾;
(3)6人排成一排,甲、乙不相邻.
当堂练习
(1)分排与直排一一对应,故排法种数为=720.
(2)甲不能排头尾,让受特殊限制的甲先选位置,有种选法,然后其他5人排,有种排法,故排法种数为 =480.
(3)甲、乙不相邻,第一步除甲、乙外的其余4人先排好;第二步,甲、乙在已排好的4人的左、右及之间的空位中排,共有=480种排法.
解析
3.用1,2,3,4,5,6,7排出无重复数字的七位数,按下述要求各有多少个?
(1)偶数不相邻;
(2)偶数一定在奇数位上;
(3)1和2之间恰夹有一个奇数,没有偶数.
当堂练习
(1)用插空法,共有=1 440个.
(2)先把偶数排在奇数位上有种排法,再排奇数有种排法,所以共有 =576个.
(3)在1和2之间放一个奇数有种方法,把1,2和相应的奇数看成整体和其他4个数进行排列有种排法,所以共有 =720个.
解析
归纳小结
直接法 把符合条件的排列数直接列式计算
优先法 优先安排特殊元素或特殊位置
捆绑法 把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
插空法 对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空当中
定序问题 除法处理 对于定序问题,可先不考虑顺序限制,排列后,再除以定序元素的全排列
间接法 正难则反,等价转化的方法
作 业
课本P27:12
复习引入
1、排列:
一般地,从个不同中取出()个元素,按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
2、排列数:
从个不同的元素中取出()个元素的所有排列的个数,叫做从个不同的元素中取出个元素的排列数.用符号表示.
3、排列数:
个不同元素全部取出的一个排列,叫做个不同元素的一个全排列.
(3)全排列数公式:
4.有关公式:
(2)排列数公式:
复习引入
(1)阶乘:
人教A版同步教材名师课件
排列与排列数
---习题课
学习目标
学 习 目 标 核心素养
通过分析、比较,掌握解排列问题的基本方法 数学运算
启发学生提升提出问题、分析问题和创造性地解决问题的能力 逻辑推理
学习目标
学习目标:
1.排列数的简单应用.
2.解排列问题的基本方法(捆绑法、插空法等)的灵活应用.
学科核心素养:
1.通过渗透分类讨论的数学思想,发展学生的逻辑推理核心素养
2通过探究与活动,明白考虑问题要细致,说理要明确,发展学生的数学抽象与数学运算核心素养
3通过对生活中的排列问题研究的过程,体会数学的实际应用价值教学重点难点
例1、用0到9这10个数字,可以组成多少个没有重复数字的三位数?
法一:由于在没有重复数字的三位数中,百位上的数字不能是0,因此可以分两步完成排列.
第1步,排百位上的数字,可以从1到9这九个数字中任选1个,有种选法.
第2步:排十位和个位上的数字,可以从余下的9个数字中任选2个,有种选法;
由分步乘法计数原理,所求的三位数的个数为×=9×9×8=648.
典例讲解
解析
法二:符合条件的三位数可分成3类.
①每一位数字都不是0的三位数有个;
②个位数字是0的三位数有个;
③十位数字是0的三位数有个;
根据分类加法计数原理:符合条件的三位数的个数为648.
典例讲解
例1、用0到9这10个数字,可以组成多少个没有重复数字的三位数?
解析
法三:从0到9这10个数字中任取3个数字的排列数为,其中0在百位上的排列数是,它们的差就是用这10个数字组成的没有重复数字的三位数的个数,即所求的三位数的个数为=
典例讲解
例1、用0到9这10个数字,可以组成多少个没有重复数字的三位数?
解析
方法归纳
不同数字的无重复排列是排列问题中的一类典型问题.其常见的附加条件有:奇偶数、倍数关系、大小关系等,也可以有相邻问题、插空问题,也可以与数列等知识相联系等.解决这类问题的关键是搞清事件是什么,元素是什么,位置是什么,给出了什么样的附加条件,然后按特殊元素(位置)的性质分类(每一类的各种方法都能保证事件的完成),按事件发生的连续过程合理分步来解决.这类问题的隐含条件“ 0不能在首位”尤其不能忽略.
变式训练
1.用0,1,2,3,4,5这六个数字,可以组成多少个分别符合下列条件的无重复数字的四位数:
(1)奇数;
(2)偶数;
(3)大于3 125的数
(1)先排个位,再排首位,共有=144(个).
(2)以0结尾的四位偶数有个,以2或4结尾的四位偶数有个,则共有+ =156(个).
(3)要比3 125大,4,5作千位时有个,3作千位,2,4,5作百位时有个,3作千位,1作百位,4,5作十位时有个,所以共有(个).
解析
例2、3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(1)全体站成一排,男、女各站在一起;
(2)全体站成一排,男生必须站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,男、女各不相邻.
典例讲解
(1)男生必须站在一起是男生的全排列,有种排法;女生必须站在一起是女生的全排列,有种排法;全体男生、女生各视为一个元素,有种排法.由分步计数原理知,共有· · =288种排队方法.
(2)三个男生全排列有种方法,把所有男生视为一个元素,与4名女生组成5个元素全排列,有种排法.故有· =720种排队方法.
解析
例2、3名男生、4名女生按照不同的要求排队,求不同的排队方法的种数.
(1)全体站成一排,男、女各站在一起;
(2)全体站成一排,男生必须站在一起;
(3)全体站成一排,男生不能站在一起;
(4)全体站成一排,男、女各不相邻.
典例讲解
(3)先安排女生,共有种排法;男生在4个女生隔成的五个空中安排,共有种排法,故共有· =1 440种排法.
(4)排好男生后让女生插空,共有· =144种排法.
解析
方法归纳
本题是“邻”与“不邻”类型的排列问题.
(1)某些元素要求不相邻时,可以先安排其他元素,再将这些不相邻元素插入空位,这种方法称为“插空法”,即“不相邻元素插空法”.
(2)对于某些元素“相邻”的排列问题,一般采用“捆绑法”,即先把相邻的若干个元素“捆绑”为一个大元素与其余元素全排列,然后再松绑,将这若干个元素内部全排列
变式训练
2.某次文艺晚会上共演出8个节目,其中2个唱歌、3个舞蹈、3个曲艺节目,求分别满足下列条件的节目编排方法有多少种?
(1)一个唱歌节目开头,另一个放在最后压台;
(2)2个唱歌节目互不相邻;
(3)2个唱歌节目相邻且3个舞蹈节目不相邻.
(1)先排唱歌节目有种排法,再排其他节目有种排法,所以共有· =1 440种排法.
(2)先排3个舞蹈节目和3个曲艺节目有种排法,再从其中7个空(包括两端)中选2个排唱歌节目,有种插入方法,所以共有· =30 240种排法.
(3)把2个相邻的唱歌节目看作一个元素,与3个曲艺节目排列共种排法,再将3个舞蹈节目插入,共有种插入方法,最后将2个唱歌节目互换位置,有种排法,故所求排法共有· · =2 880种排法.
解析
例3、某一天的课程表要排入政治、语文、数学、物理、体育、美术共六节课,如果第一节不排体育,最后一节不排数学,那么共有多少种不同课程表的排法?
典例讲解
法一:6门课总的排法是种,其中不符合要求的可分为:
体育排在第一节有种排法,如图中Ⅰ;
数学排在最后一节有种排法,如图中Ⅱ;
但这两种方法,都包括体育在第一节,数学排在最后一节,如图中Ⅲ,这种情况有种排法;
因此符合条件的排法应是:504(种).
解析
典例讲解
法二:根据要求,课程表安排可分为4种情况:
(1)体育、数学既不排在第一节也不排在最后一节,这种情况有· 种排法;
(2)数学排在第一节但体育不排在最后一节,有· 种排法;
(3)体育排在最后一节但数学不排在第一节,有· 种排法;
(4)数学排在第一节,体育排在最后一节,有种排法.
这四类排法并列,不重复也不遗漏,故总的排法有:
· + · + · + =504(种).
例3、某一天的课程表要排入政治、语文、数学、物理、体育、美术共六节课,如果第一节不排体育,最后一节不排数学,那么共有多少种不同课程表的排法?
解析
方法归纳
本题是属于“在”与“不在”问题,是排列问题中的常见类型,常用“元素分析法”“位置分析法”.当题目中有两个约束条件时,往往考虑一个约束条件的同时,还需要考虑另一个约束条件,这就要进行正确的分类,有时分的类较多,用直接法较麻烦,往往采用“间接法”.
变式训练
设,且成等差数列,则,即应是偶数.因此从1到20这20个数字中任选出三个数成等差数列,则第一个数与第三个数必同为偶数或同为奇数,而1到20这20个数字中有10个偶数和10个奇数.当第一个和第三个数选定后,中间数被唯一确定.因此,选法只有两类:
(1)第一、三个数都是偶数,有种选法;
(2)第一、三个数都是奇数,有种选法;
于是,选出3个数成等差数列的个数为+ =180(个).
3.从集合{1,2,3,…,20}中任选出3个不同的数,使这3个数成等差数列,这样的等差数列可以有多少个?
解析
1.对有约束条件的排列问题,应注意如下类型:
⑴某些元素不能在或必须排列在某一位置;
⑵某些元素要求连排(即必须相邻);
⑶某些元素要求分离(即不能相邻);
2.基本的解题方法:
(1)有特殊元素或特殊位置的排列问题,通常是先排特殊元素或特殊位置,称为优先处理特殊元素(位置)法(优先法);
特殊元素,特殊位置优先安排策略
素养提炼
素养提炼
(3)某些元素不相邻排列时,可以先排其他元素,再将这些不相邻元素插入空挡,这种方法称为“插空法”;
不相邻问题插空处理的策略
(2)某些元素要求必须相邻时,可以先将这些元素看作一个元素,与其他元素排列后,再考虑相邻元素的内部排列,这种方法称为“捆绑法”;
相邻问题捆绑处理的策略
当堂练习
1.六个停车位置,有3辆汽车需要停放,若要使三个空位连在一起,则停放的方法数为________.
把3个空位看作一个元素,与3辆汽车共有4个元素全排列,故停放的方法有=4×3×2×1=24种.
24
解析
2.分别求出符合下列要求的不同排法的种数.
(1)6名学生排3排,前排1人,中排2人,后排3人;
(2)6名学生排成一排,甲不在排头也不在排尾;
(3)6人排成一排,甲、乙不相邻.
当堂练习
(1)分排与直排一一对应,故排法种数为=720.
(2)甲不能排头尾,让受特殊限制的甲先选位置,有种选法,然后其他5人排,有种排法,故排法种数为 =480.
(3)甲、乙不相邻,第一步除甲、乙外的其余4人先排好;第二步,甲、乙在已排好的4人的左、右及之间的空位中排,共有=480种排法.
解析
3.用1,2,3,4,5,6,7排出无重复数字的七位数,按下述要求各有多少个?
(1)偶数不相邻;
(2)偶数一定在奇数位上;
(3)1和2之间恰夹有一个奇数,没有偶数.
当堂练习
(1)用插空法,共有=1 440个.
(2)先把偶数排在奇数位上有种排法,再排奇数有种排法,所以共有 =576个.
(3)在1和2之间放一个奇数有种方法,把1,2和相应的奇数看成整体和其他4个数进行排列有种排法,所以共有 =720个.
解析
归纳小结
直接法 把符合条件的排列数直接列式计算
优先法 优先安排特殊元素或特殊位置
捆绑法 把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
插空法 对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空当中
定序问题 除法处理 对于定序问题,可先不考虑顺序限制,排列后,再除以定序元素的全排列
间接法 正难则反,等价转化的方法
作 业
课本P27:12
