人教A版(2019)高中数学选择性必修第三册 《组合与组合数---第一课时》名师课件(共34张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 《组合与组合数---第一课时》名师课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 10:24:51 | ||
图片预览










文档简介
(共34张PPT)
复习引入
问题一:从甲、乙、丙3名同学中选出2名去参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的选法
问题二:从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法
甲、乙;甲、丙;乙、丙
3
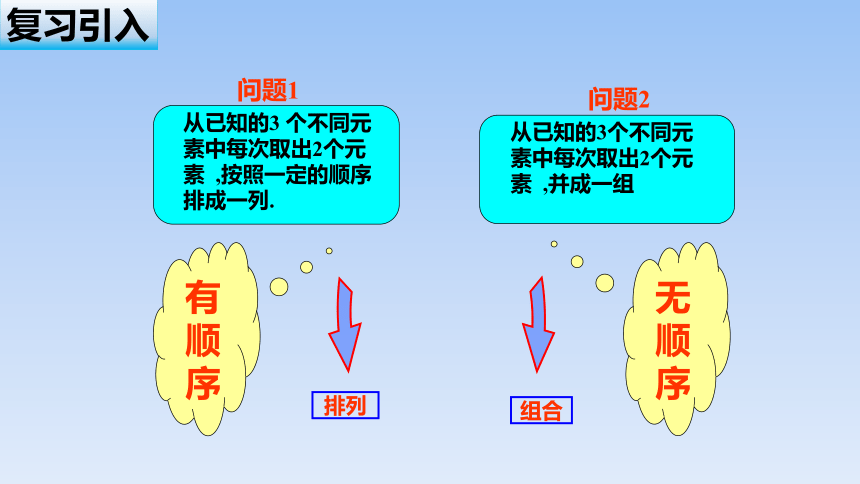
复习引入
从已知的3个不同元素中每次取出2个元素 ,并成一组
问题2
从已知的3 个不同元素中每次取出2个元素 ,按照一定的顺序排成一列.
问题1
排列
组合
有
顺
序
无
顺
序
人教A版同步教材名师课件
组合与组合数
学习目标
学 习 目 标 核心素养
结合实例,理解组合与组合数的概念,明确排列与组合的联系与区别,能判断一个问题是排列问题还是组合问题 数学抽象
会利用排列的知识推导组合数公式,理解排列数与组合数之间的联系,掌握组合数的性质并能进行简单应用 数学运算
学习目标
学习目标:
1.了解组合与排列的区别与联系.
2.理解组合的概念、组合数公式及性质.
3.能利用组合的概念及组合数公式解决实际问题.
学科核心素养:
1.经历组合与组合数的概念和性质的探究过程,比较排列与组合的区别,发展学生的数学抽象核心素养.
2.在应用组合数公式解决计算问题的过程中,发展学生的数学运算核心素养.
探究新知
从甲、乙、丙3名同学中选2名去参加一项活动,有多少种不同的选法 这一问题与6.2.1节的问题1有什么联系与区别
在6.2.1节问题1的6种选法中,存在“甲上午、乙下午” 和“乙上午、甲下午” 2种不同顺序的选法,我们可以将它看成是先选出甲、乙2名同学,然后再分配上午和下午而得到的,同样,先选出甲、丙或乙、丙,再分配上午和下午也都各有2种方法.而从甲、乙、丙3名同学中选2名去参加一项活动,就只需考虑将选出的2名同学作为一组,不需要考虑他们的顺序,于是,在6.2.1节问题1的6种选法中,将选出的2名同学作为一组的选法就只有如下3种情况:甲乙,甲丙,乙丙.
将具体背景舍去,上述问题可以概括为:从3个不同元素中取出2个元素作为一组,一共有多少个不同的组
思考
这就是今天我们要研究的问题.
一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
排列与组合的概念有什么共同点与不同点
组合定义:
探究新知
组合定义: 一般地,从个不同元素中取出个元素并成一组,叫做从个不同元素中取出个元素的一个组合.
排列定义: 一般地,从个不同元素中取出个元素,按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
共同点: 都要“从个不同元素中取出个元素”
不同点: 排列与元素的顺序有关,
而组合则与元素的顺序无关.
探究新知
思考一:与是相同的排列还是相同的组合 为什么
思考二:两个相同的排列有什么特点 两个相同的组合呢
构造排列分成两步完成,先取后排;而构造组合就是其中一个步骤.
思考三:组合与排列有联系吗
探究新知
元素相同
1)元素相同;
2)元素排列顺序相同.
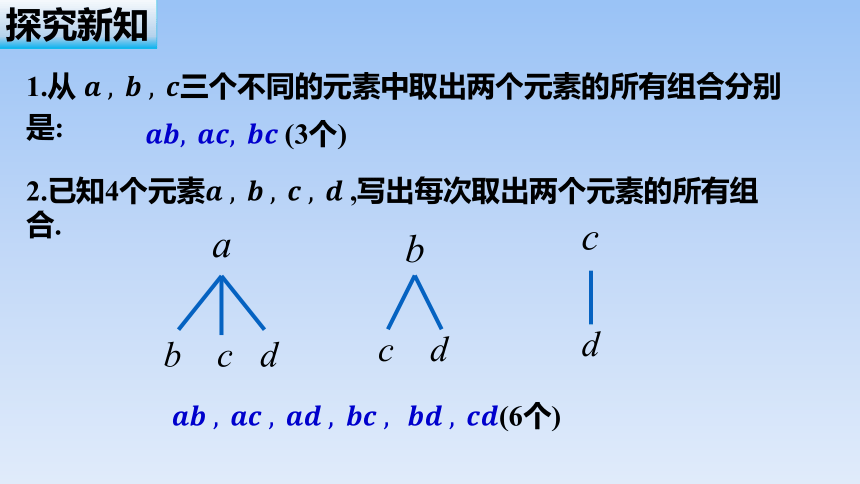
1.从 三个不同的元素中取出两个元素的所有组合分别是:
(3个)
2.已知4个元素,写出每次取出两个元素的所有组合.
a
b c d
b
c d
c
d
(6个)
探究新知
例1.判断下列问题是组合问题还是排列问题
(1)设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个
(2)某铁路线上有5个车站,则这条铁路线上共需准备多少种车票
有多少种不同的火车票价
组合问题
排列问题
(3)10名同学分成人数相同的数学和英语两个学习小组,共有多少种分法
组合问题
(4)10人聚会,见面后每两人之间要握手相互问候,共需握手多少次
组合问题
(5)从4个风景点中选出2个游览,有多少种不同的方法
组合问题
(6)从4个风景点中选出2个,并确定这2个风景点的游览顺序,有多少种不同的方法
排列问题
组合问题
组合是选择的结果,排列是
选择后再排序的结果.
典例讲解
方法归纳
判断一个问题是否是组合问题的方法技巧
区分排列与组合的关键是看结果是否与元素的顺序有关,若交换某两个元素的位置对结果产生影响,则是排列问题,而交换任意两个元素的位置对结果没有影响,则是组合问题,也就是说排列问题与选取元素的顺序有关,组合问题与选取元素的顺序无关.由此可知,定序问题属于组合,即排列时,如果限定某些元素保持规定的顺序,则定序的这n个元素属于组合问题.
变式训练
1.判断下列问题是排列问题,还是组合问题.
(1)从1,2,3,…,9九个数字中任取3个,组成一个三位数,这样的三位数共有多少个
(2)从1,2,3,…,9九个数字中任取3个,然后把这三个数字相加得到一个和,这样的和共有多少个
(3)从四名学生中选2名去完成同一件工作,有多少种不同的选法
(4)5个人规定相互通话一次,共通了多少次电话
(5)5个人相互各写一封信,共写了多少封信
(1)当取出3个数字后,如果改变三个数字的顺序,会得到不同的三位数,此问题不但与取出元素有关,而且与元素的安排顺序有关,是排列问题.
(2)取出3个数字之后,无论怎样改变这三个数字之间的顺序,其和均不变,此问题只与取出元素有关,而与元素的安排顺序无关,是组合问题.
解析
变式训练
(3)2名学生完成的是同一件工作,没有顺序,是组合问题.
(4)甲与乙通一次电话,也就是乙与甲通一次电话,无顺序区别,为组合问题.
(5)发信人与收信人是有区别的,是排列问题.
1.判断下列问题是排列问题,还是组合问题.
(1)从1,2,3,…,9九个数字中任取3个,组成一个三位数,这样的三位数共有多少个
(2)从1,2,3,…,9九个数字中任取3个,然后把这三个数字相加得到一个和,这样的和共有多少个
(3)从四名学生中选2名去完成同一件工作,有多少种不同的选法
(4)5个人规定相互通话一次,共通了多少次电话
(5)5个人相互各写一封信,共写了多少封信
解析
探究新知
如:从 a , b , c三个不同的元素中取出两个元素的所有组合个数是:
如:已知4个元素a , b , c , d ,写出每次取出两个
元素的所有组合个数是:
组合数:
注意:
是一个数,应该把它与"组合"区别开来.
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号表示.
组合数公式:
排列与组合是有区别的,但它们又有联系.
根据分步计数原理,得到:
因此:
探究新知
这里n,m∈N*,且,这个公式叫做组合数公式.
一般地,求从个不同元素中取出个元素的排列数,可以分为以下2步:
第1步,先求出从这个不同元素中取出个元素的组合数.
第2步,求每一个组合中个元素的全排列数.
我们规定:
性质1
证明:
性质2
证明:
探究新知
注:1 公式特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与原组合数上标较大的相同的一个组合数.
2 此性质的作用:恒等变形,简化运算.在今后学习"二项式定理"时,我们会看到它的主要应用.
探究新知
典例讲解
例2.计算下列各式的值.
(1) ;
(2) ;
(3) .
(1).
(2)利用组合数的性质,
则
=
=
…==329.
解析
典例讲解
解析
例2.计算下列各式的值.
(1) ;
(2) ;
(3) .
方法归纳
(1)涉及具体数字的可以直接用进行计算.
(2)涉及字母的可以用阶乘式= 计算.
(3)计算时应注意利用组合数的性质简化运算
关于组合数公式的选取技巧
2.计算.
(1) ;
(2) ;
(3) .
(1) .
(2)原式=
=
= =462.
变式训练
解析
(3)由组合数中的限制条件可知
解得,因为,所以.
当时,原式=1=46;
当时,原式=;
当时,原式= 1=46.
2.计算.
(1) ;
(2) ;
(3) .
变式训练
解析
典例讲解
例3、在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法
(1)任意选5人;
(2)甲、乙、丙三人必须参加;
(3)甲、乙、丙三人不能参加;
(4)甲、乙、丙三人只能有1人参加.
(1)从中任取5人是组合问题,共有=792种不同的选法.
(2)甲、乙、丙三人必须参加,则只需要从另外9人中选2人,是组合问题,共有=36种不同的选法.
(3)甲、乙、丙三人不能参加,则只需从另外的9人中选5人,共有=126种不同的选法.
解析
典例讲解
例3、在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法
(1)任意选5人;
(2)甲、乙、丙三人必须参加;
(3)甲、乙、丙三人不能参加;
(4)甲、乙、丙三人只能有1人参加.
(4)甲、乙、丙三人只能有1人参加,可分两步:先从甲、乙、丙中选1人,有=3种选法;再从另外9人中选4人,有种选法.共有=378种不同的选法.
解析
方法归纳
解答简单的组合问题的思考方法:
(1)弄清要做的这件事是什么事;
(2)选出的元素是否与顺序有关,也就是看看是不是组合问题;
(3)结合两计数原理利用组合数公式求出结果.
变式训练
3.一个口袋内装有大小相同的7个白球和1个黑球.
(1)从口袋内取出3个球,共有多少种取法
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法
(1)从口袋内的8个球中取出3个球,取法种数是.
(2)从口袋内取出3个球有1个是黑球,于是还要从7个白球中再取出2个,取法种数是.
(3)由于所取出的3个球中不含黑球,也就是要从7个白球中取出3个球,取法种数是35.
解析
素养提炼
形式 适用范围
乘积式 含具体数字的组合数的求值
阶乘式 含字母的组合数的有关变形及证明
1.组合数公式的两种形式的适用范围
2.组合数的两个性质及其关注点
性质1: .
它反映了组合数的对称性.若m>,通常不直接计算,而改为计算,这样可以减少计算量.
素养提炼
性质2: .
特点是左端下标为n+1,右端下标都为n,相差1;左端的上标与右端上标的一个一样,右端的另一个上标比它们少1.
要注意性质的顺用、逆用、变形用.
顺用是将一个组合数拆成两个;逆用则是"合二为一";变形式的使用,为某些项相互抵消提供了方便,在解题中要注意灵活运用.
当堂练习
1.在下列问题中,哪些是组合问题 哪些是排列问题
(1)从四名学生中选出2名学生完成两件不同的工作,有多少种不同的选法
(2)四支足球队之间进行单循环比赛,共需赛多少场
(3)四支足球队争夺冠亚军,有多少种不同的结果
(1)2名学生完成两件不同的工作,有顺序,是排列问题.
(2)单循环比赛要求每两支球队之间只打一场比赛,没有顺序,是组合问题.
(3)争夺冠亚军是有顺序的,是排列问题.
解析
当堂练习
2.解方程:.
解得或(舍去),经检验是原方程的解.
原方程可化为,即,
∴,
∴,
∴,
解析
当堂练习
3.从6位同学中选出4位参加一个座谈会,要求张、王两同学中至多有一个人参加,则不同选法的种数为( )
A.9 B.14 C.12 D.15
法一:(直接法)分两类:
第1类,张、王两同学都不参加,有=1种选法;
第2类,张、王两同学中只有1人参加,有=8种选法.
故共有1+8=9种选法.
法二:(间接法)共有- =9种不同选法.
解析
A
归纳小结
组合与组合数的概念
组合的概念
组合数
与排列的区别
公式
性质
作 业
课本P22练习:2,3
复习引入
问题一:从甲、乙、丙3名同学中选出2名去参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的选法
问题二:从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法
甲、乙;甲、丙;乙、丙
3
复习引入
从已知的3个不同元素中每次取出2个元素 ,并成一组
问题2
从已知的3 个不同元素中每次取出2个元素 ,按照一定的顺序排成一列.
问题1
排列
组合
有
顺
序
无
顺
序
人教A版同步教材名师课件
组合与组合数
学习目标
学 习 目 标 核心素养
结合实例,理解组合与组合数的概念,明确排列与组合的联系与区别,能判断一个问题是排列问题还是组合问题 数学抽象
会利用排列的知识推导组合数公式,理解排列数与组合数之间的联系,掌握组合数的性质并能进行简单应用 数学运算
学习目标
学习目标:
1.了解组合与排列的区别与联系.
2.理解组合的概念、组合数公式及性质.
3.能利用组合的概念及组合数公式解决实际问题.
学科核心素养:
1.经历组合与组合数的概念和性质的探究过程,比较排列与组合的区别,发展学生的数学抽象核心素养.
2.在应用组合数公式解决计算问题的过程中,发展学生的数学运算核心素养.
探究新知
从甲、乙、丙3名同学中选2名去参加一项活动,有多少种不同的选法 这一问题与6.2.1节的问题1有什么联系与区别
在6.2.1节问题1的6种选法中,存在“甲上午、乙下午” 和“乙上午、甲下午” 2种不同顺序的选法,我们可以将它看成是先选出甲、乙2名同学,然后再分配上午和下午而得到的,同样,先选出甲、丙或乙、丙,再分配上午和下午也都各有2种方法.而从甲、乙、丙3名同学中选2名去参加一项活动,就只需考虑将选出的2名同学作为一组,不需要考虑他们的顺序,于是,在6.2.1节问题1的6种选法中,将选出的2名同学作为一组的选法就只有如下3种情况:甲乙,甲丙,乙丙.
将具体背景舍去,上述问题可以概括为:从3个不同元素中取出2个元素作为一组,一共有多少个不同的组
思考
这就是今天我们要研究的问题.
一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
排列与组合的概念有什么共同点与不同点
组合定义:
探究新知
组合定义: 一般地,从个不同元素中取出个元素并成一组,叫做从个不同元素中取出个元素的一个组合.
排列定义: 一般地,从个不同元素中取出个元素,按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
共同点: 都要“从个不同元素中取出个元素”
不同点: 排列与元素的顺序有关,
而组合则与元素的顺序无关.
探究新知
思考一:与是相同的排列还是相同的组合 为什么
思考二:两个相同的排列有什么特点 两个相同的组合呢
构造排列分成两步完成,先取后排;而构造组合就是其中一个步骤.
思考三:组合与排列有联系吗
探究新知
元素相同
1)元素相同;
2)元素排列顺序相同.
1.从 三个不同的元素中取出两个元素的所有组合分别是:
(3个)
2.已知4个元素,写出每次取出两个元素的所有组合.
a
b c d
b
c d
c
d
(6个)
探究新知
例1.判断下列问题是组合问题还是排列问题
(1)设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个
(2)某铁路线上有5个车站,则这条铁路线上共需准备多少种车票
有多少种不同的火车票价
组合问题
排列问题
(3)10名同学分成人数相同的数学和英语两个学习小组,共有多少种分法
组合问题
(4)10人聚会,见面后每两人之间要握手相互问候,共需握手多少次
组合问题
(5)从4个风景点中选出2个游览,有多少种不同的方法
组合问题
(6)从4个风景点中选出2个,并确定这2个风景点的游览顺序,有多少种不同的方法
排列问题
组合问题
组合是选择的结果,排列是
选择后再排序的结果.
典例讲解
方法归纳
判断一个问题是否是组合问题的方法技巧
区分排列与组合的关键是看结果是否与元素的顺序有关,若交换某两个元素的位置对结果产生影响,则是排列问题,而交换任意两个元素的位置对结果没有影响,则是组合问题,也就是说排列问题与选取元素的顺序有关,组合问题与选取元素的顺序无关.由此可知,定序问题属于组合,即排列时,如果限定某些元素保持规定的顺序,则定序的这n个元素属于组合问题.
变式训练
1.判断下列问题是排列问题,还是组合问题.
(1)从1,2,3,…,9九个数字中任取3个,组成一个三位数,这样的三位数共有多少个
(2)从1,2,3,…,9九个数字中任取3个,然后把这三个数字相加得到一个和,这样的和共有多少个
(3)从四名学生中选2名去完成同一件工作,有多少种不同的选法
(4)5个人规定相互通话一次,共通了多少次电话
(5)5个人相互各写一封信,共写了多少封信
(1)当取出3个数字后,如果改变三个数字的顺序,会得到不同的三位数,此问题不但与取出元素有关,而且与元素的安排顺序有关,是排列问题.
(2)取出3个数字之后,无论怎样改变这三个数字之间的顺序,其和均不变,此问题只与取出元素有关,而与元素的安排顺序无关,是组合问题.
解析
变式训练
(3)2名学生完成的是同一件工作,没有顺序,是组合问题.
(4)甲与乙通一次电话,也就是乙与甲通一次电话,无顺序区别,为组合问题.
(5)发信人与收信人是有区别的,是排列问题.
1.判断下列问题是排列问题,还是组合问题.
(1)从1,2,3,…,9九个数字中任取3个,组成一个三位数,这样的三位数共有多少个
(2)从1,2,3,…,9九个数字中任取3个,然后把这三个数字相加得到一个和,这样的和共有多少个
(3)从四名学生中选2名去完成同一件工作,有多少种不同的选法
(4)5个人规定相互通话一次,共通了多少次电话
(5)5个人相互各写一封信,共写了多少封信
解析
探究新知
如:从 a , b , c三个不同的元素中取出两个元素的所有组合个数是:
如:已知4个元素a , b , c , d ,写出每次取出两个
元素的所有组合个数是:
组合数:
注意:
是一个数,应该把它与"组合"区别开来.
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号表示.
组合数公式:
排列与组合是有区别的,但它们又有联系.
根据分步计数原理,得到:
因此:
探究新知
这里n,m∈N*,且,这个公式叫做组合数公式.
一般地,求从个不同元素中取出个元素的排列数,可以分为以下2步:
第1步,先求出从这个不同元素中取出个元素的组合数.
第2步,求每一个组合中个元素的全排列数.
我们规定:
性质1
证明:
性质2
证明:
探究新知
注:1 公式特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与原组合数上标较大的相同的一个组合数.
2 此性质的作用:恒等变形,简化运算.在今后学习"二项式定理"时,我们会看到它的主要应用.
探究新知
典例讲解
例2.计算下列各式的值.
(1) ;
(2) ;
(3) .
(1).
(2)利用组合数的性质,
则
=
=
…==329.
解析
典例讲解
解析
例2.计算下列各式的值.
(1) ;
(2) ;
(3) .
方法归纳
(1)涉及具体数字的可以直接用进行计算.
(2)涉及字母的可以用阶乘式= 计算.
(3)计算时应注意利用组合数的性质简化运算
关于组合数公式的选取技巧
2.计算.
(1) ;
(2) ;
(3) .
(1) .
(2)原式=
=
= =462.
变式训练
解析
(3)由组合数中的限制条件可知
解得,因为,所以.
当时,原式=1=46;
当时,原式=;
当时,原式= 1=46.
2.计算.
(1) ;
(2) ;
(3) .
变式训练
解析
典例讲解
例3、在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法
(1)任意选5人;
(2)甲、乙、丙三人必须参加;
(3)甲、乙、丙三人不能参加;
(4)甲、乙、丙三人只能有1人参加.
(1)从中任取5人是组合问题,共有=792种不同的选法.
(2)甲、乙、丙三人必须参加,则只需要从另外9人中选2人,是组合问题,共有=36种不同的选法.
(3)甲、乙、丙三人不能参加,则只需从另外的9人中选5人,共有=126种不同的选法.
解析
典例讲解
例3、在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法
(1)任意选5人;
(2)甲、乙、丙三人必须参加;
(3)甲、乙、丙三人不能参加;
(4)甲、乙、丙三人只能有1人参加.
(4)甲、乙、丙三人只能有1人参加,可分两步:先从甲、乙、丙中选1人,有=3种选法;再从另外9人中选4人,有种选法.共有=378种不同的选法.
解析
方法归纳
解答简单的组合问题的思考方法:
(1)弄清要做的这件事是什么事;
(2)选出的元素是否与顺序有关,也就是看看是不是组合问题;
(3)结合两计数原理利用组合数公式求出结果.
变式训练
3.一个口袋内装有大小相同的7个白球和1个黑球.
(1)从口袋内取出3个球,共有多少种取法
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法
(1)从口袋内的8个球中取出3个球,取法种数是.
(2)从口袋内取出3个球有1个是黑球,于是还要从7个白球中再取出2个,取法种数是.
(3)由于所取出的3个球中不含黑球,也就是要从7个白球中取出3个球,取法种数是35.
解析
素养提炼
形式 适用范围
乘积式 含具体数字的组合数的求值
阶乘式 含字母的组合数的有关变形及证明
1.组合数公式的两种形式的适用范围
2.组合数的两个性质及其关注点
性质1: .
它反映了组合数的对称性.若m>,通常不直接计算,而改为计算,这样可以减少计算量.
素养提炼
性质2: .
特点是左端下标为n+1,右端下标都为n,相差1;左端的上标与右端上标的一个一样,右端的另一个上标比它们少1.
要注意性质的顺用、逆用、变形用.
顺用是将一个组合数拆成两个;逆用则是"合二为一";变形式的使用,为某些项相互抵消提供了方便,在解题中要注意灵活运用.
当堂练习
1.在下列问题中,哪些是组合问题 哪些是排列问题
(1)从四名学生中选出2名学生完成两件不同的工作,有多少种不同的选法
(2)四支足球队之间进行单循环比赛,共需赛多少场
(3)四支足球队争夺冠亚军,有多少种不同的结果
(1)2名学生完成两件不同的工作,有顺序,是排列问题.
(2)单循环比赛要求每两支球队之间只打一场比赛,没有顺序,是组合问题.
(3)争夺冠亚军是有顺序的,是排列问题.
解析
当堂练习
2.解方程:.
解得或(舍去),经检验是原方程的解.
原方程可化为,即,
∴,
∴,
∴,
解析
当堂练习
3.从6位同学中选出4位参加一个座谈会,要求张、王两同学中至多有一个人参加,则不同选法的种数为( )
A.9 B.14 C.12 D.15
法一:(直接法)分两类:
第1类,张、王两同学都不参加,有=1种选法;
第2类,张、王两同学中只有1人参加,有=8种选法.
故共有1+8=9种选法.
法二:(间接法)共有- =9种不同选法.
解析
A
归纳小结
组合与组合数的概念
组合的概念
组合数
与排列的区别
公式
性质
作 业
课本P22练习:2,3
