人教A版(2019)高中数学选择性必修第三册 6.2.3_组合课件(共24张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 6.2.3_组合课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 10:31:13 | ||
图片预览








文档简介
(共24张PPT)
6.2.3 组 合
1.理解组合及组合数的概念.
2.能利用计数原理推导组合数公式,并会应用公式解决简单的组合问题.
问题导学
题型探究
达标检测
学习目标
答案
问题导学 新知探究 点点落实
知识点一 组合的定义
思考 ①从3,5,7,11中任取两个数相除;
②从3,5,7,11中任取两个数相乘.
以上两个问题中哪个是排列?①与②有何不同特点?
答案 ①是排列,①中选取的两个数是有序的,②中选取的两个数是无需排列.
从n个不同元素中取出m(m≤n)个元素 ,叫做从n个不同元素中取出m个元素的一个组合.
合成一组
答案
知识点二 组合数与组合数公式
从3,5,7,11中任取两个数相除
思考1 可以得到多少个不同的商?
思考2 如何用分步乘法计数原理求商的个数?
组合数定义 及表示 从n个不同元素中取出m(m≤n)个元素的 ,
叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
组合数 公式 乘积 形式
=_______________________
阶乘 形式
=____________
性质 =_____
=___+_____
备注 规定 =__
所有不同组合的个数
1
答案
返回
类型一 组合概念的理解
例1 判断下列问题是组合问题还是排列问题?
(1)设集合A={a,b,c,d},则集合A的含有3个元素的子集有多少个?
(2)某铁路线上有4个车站,则这条铁路线上需准备多少种车票?
(3)从7本不同的书中取出5本给某同学.
(4)3人去做5种不同的工作,每人做一种,有多少种分工方法?
(5)把3本相同的书分给5个学生,每人最多得一本,有多少种分配方法?
解析答案
题型探究 重点难点 个个击破
反思与感悟
解 (1)因为集合A的任一个含3个元素的子集与元素顺序无关,故它是组合问题.
(2)一种火车票与起点、终点顺序有关,例“甲→乙”与“乙→甲”的车票不同,故它是排列问题.
(3)从7本不同的书中取出5本给某同学,在每种取法中取出的5本书并不考虑书的顺序,故它是组合问题.
(4)因为一种分工方法就是从5种不同工作中取出3种,按一定顺序分给3人去干,故它是排列问题.
(5)因为3本书是相同的,把3本书无论分给哪三个人都不需考虑顺序,
故它是组合问题.故(1)(3)(5)是组合问题,(2)(4)是排列问题.
反思与感悟
反思与感悟
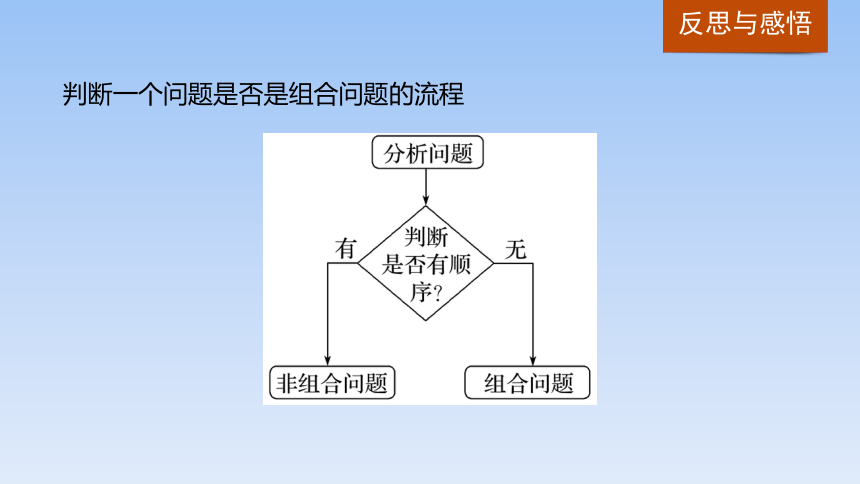
判断一个问题是否是组合问题的流程
解析答案
跟踪训练1 给出下列问题:
(1)从a,b,c,d四名学生中选2名学生完成一件工作,有多少种不同的选法?
(2)从a,b,c,d四名学生中选2名学生完成两件不同的工作,有多少种不同的选法?
(3)a,b,c,d四支足球队之间进行单循环比赛,共需赛多少场?
(4)a,b,c,d四支足球队争夺冠亚军,有多少种不同的结果?
(5)某人射击8枪,命中4枪,且命中的4枪均为2枪连中,不同的结果有多少种?
(6)某人射击8枪,命中4枪,且命中的4枪中恰有3枪连中,不同的结果有多少种?
在上述问题中,________是组合问题,________是排列问题.
解析 (1)2名学生完成的是同一件工作,没有顺序,是组合问题.
(2)2名学生完成两件不同的工作,有顺序,是排列问题.
(3)单循环比赛要求每两支球队之间只打一场比赛,没有顺序,是组合问题.
(4)冠亚军是有顺序的,是排列问题.
(5)命中的4枪均为2枪连中,没有顺序,是组合问题.
(6)命中的4枪中恰有3枪连中,即连中3枪和单中1枪,有顺序,是排列问题.
答案 (1)(3)(5) (2)(4)(6)
解析答案
类型二 组合的列举问题
例2 从5个不同元素a,b,c,d,e中取出2个,列出所有组合为________
______________________________.
解析 要想列出所有组合,做到不重不漏,先将元素按照一定顺序排好,然后按顺序用图示的方法将各个组合逐个地标示出来.如图所示.
ab,ac,
ad,ae,bc,bd,be,cd,ce,de
反思与感悟
反思与感悟 用树形图来写所有组合时,当前面的元素写完后,后面再不能出现该元素,要避免重复和遗漏.
解析答案
跟踪训练2 写出从A,B,C,D,E 5个元素中,依次取3个元素的所有组合.
解 所有组合为ABC、ABD、ABE、ACD、ACE、ADE、BCD、BCE、BDE、CDE.
解析答案
类型三 组合数公式及应用
角度1 有关组合数的计算与证明
反思与感悟
反思与感悟
解析答案
C
210
解析答案
角度2 含组合数的方程或不等式
即m2-23m+42=0
解得:m=2或21.
∵0≤m≤5,∴m=2,
解析答案
∴该不等式的解集为{6,7,8,9}.
反思与感悟
1.解答(1)易忽略根的检验而产生增根的错误,(2)易忽略n∈N*而导致错误.
2.与排列组合有关的方程或不等式问题要用到排列数、组合数公式,以及组合数的性质,求解时,要注意由 中的m∈N*,n∈N*,且n≥m确定m、n的范围,因此求解后要验证所得结果是否适合题意.
反思与感悟
所以(x-3)(x-6)=5×4×2=8×5.
所以x=11或x=-2(舍去负根).
经检验符合题意,所以方程的解为x=11.
解析答案
返回
解析答案
达标检测
1.下列问题中,组合问题的个数是( )
①从全班50人中选出5人组成班委会;②从全班50人中选出5人分别担任班长、副班长、团支部书记、学习委员、生活委员;③从1,2,3,…,9中任取出两个数求积;④从1,2,3,…,9中任取出两个数求差或商.
A.1 B.2 C.3 D.4
解析 对于①,从50人中选出5人组成班委会,不考虑顺序是组合问题.
②为排列问题.
对于③,从1,2,3,…,9中任取两个数求积是组合问题.
因为乘法满足交换律,而减法和除法不满足,故④为排列问题.
1
2
3
4
B
解析答案
解析 依题意,有x2-x=5x-5或x2-x+5x-5=16,解得x=1或5;
x=-7或x=3.
经检验知,只有x=1或x=3符合题意.
B
1
2
3
4
解析答案
解析 由题意知3≤n≤12,且n∈N*,
∴n=3,4,5,6,7.
D
1
2
3
4
4.下列等式不正确的是( )
D
答案
1
2
3
4
返回
规律与方法
1.排列与组合的联系与区别
(1)联系:二者都是从n个不同的元素中取m(m≤n)个元素.
(2)区别:排列问题中元素有序,组合问题中元素无序.
2.关于组合数的计算
6.2.3 组 合
1.理解组合及组合数的概念.
2.能利用计数原理推导组合数公式,并会应用公式解决简单的组合问题.
问题导学
题型探究
达标检测
学习目标
答案
问题导学 新知探究 点点落实
知识点一 组合的定义
思考 ①从3,5,7,11中任取两个数相除;
②从3,5,7,11中任取两个数相乘.
以上两个问题中哪个是排列?①与②有何不同特点?
答案 ①是排列,①中选取的两个数是有序的,②中选取的两个数是无需排列.
从n个不同元素中取出m(m≤n)个元素 ,叫做从n个不同元素中取出m个元素的一个组合.
合成一组
答案
知识点二 组合数与组合数公式
从3,5,7,11中任取两个数相除
思考1 可以得到多少个不同的商?
思考2 如何用分步乘法计数原理求商的个数?
组合数定义 及表示 从n个不同元素中取出m(m≤n)个元素的 ,
叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
组合数 公式 乘积 形式
=_______________________
阶乘 形式
=____________
性质 =_____
=___+_____
备注 规定 =__
所有不同组合的个数
1
答案
返回
类型一 组合概念的理解
例1 判断下列问题是组合问题还是排列问题?
(1)设集合A={a,b,c,d},则集合A的含有3个元素的子集有多少个?
(2)某铁路线上有4个车站,则这条铁路线上需准备多少种车票?
(3)从7本不同的书中取出5本给某同学.
(4)3人去做5种不同的工作,每人做一种,有多少种分工方法?
(5)把3本相同的书分给5个学生,每人最多得一本,有多少种分配方法?
解析答案
题型探究 重点难点 个个击破
反思与感悟
解 (1)因为集合A的任一个含3个元素的子集与元素顺序无关,故它是组合问题.
(2)一种火车票与起点、终点顺序有关,例“甲→乙”与“乙→甲”的车票不同,故它是排列问题.
(3)从7本不同的书中取出5本给某同学,在每种取法中取出的5本书并不考虑书的顺序,故它是组合问题.
(4)因为一种分工方法就是从5种不同工作中取出3种,按一定顺序分给3人去干,故它是排列问题.
(5)因为3本书是相同的,把3本书无论分给哪三个人都不需考虑顺序,
故它是组合问题.故(1)(3)(5)是组合问题,(2)(4)是排列问题.
反思与感悟
反思与感悟
判断一个问题是否是组合问题的流程
解析答案
跟踪训练1 给出下列问题:
(1)从a,b,c,d四名学生中选2名学生完成一件工作,有多少种不同的选法?
(2)从a,b,c,d四名学生中选2名学生完成两件不同的工作,有多少种不同的选法?
(3)a,b,c,d四支足球队之间进行单循环比赛,共需赛多少场?
(4)a,b,c,d四支足球队争夺冠亚军,有多少种不同的结果?
(5)某人射击8枪,命中4枪,且命中的4枪均为2枪连中,不同的结果有多少种?
(6)某人射击8枪,命中4枪,且命中的4枪中恰有3枪连中,不同的结果有多少种?
在上述问题中,________是组合问题,________是排列问题.
解析 (1)2名学生完成的是同一件工作,没有顺序,是组合问题.
(2)2名学生完成两件不同的工作,有顺序,是排列问题.
(3)单循环比赛要求每两支球队之间只打一场比赛,没有顺序,是组合问题.
(4)冠亚军是有顺序的,是排列问题.
(5)命中的4枪均为2枪连中,没有顺序,是组合问题.
(6)命中的4枪中恰有3枪连中,即连中3枪和单中1枪,有顺序,是排列问题.
答案 (1)(3)(5) (2)(4)(6)
解析答案
类型二 组合的列举问题
例2 从5个不同元素a,b,c,d,e中取出2个,列出所有组合为________
______________________________.
解析 要想列出所有组合,做到不重不漏,先将元素按照一定顺序排好,然后按顺序用图示的方法将各个组合逐个地标示出来.如图所示.
ab,ac,
ad,ae,bc,bd,be,cd,ce,de
反思与感悟
反思与感悟 用树形图来写所有组合时,当前面的元素写完后,后面再不能出现该元素,要避免重复和遗漏.
解析答案
跟踪训练2 写出从A,B,C,D,E 5个元素中,依次取3个元素的所有组合.
解 所有组合为ABC、ABD、ABE、ACD、ACE、ADE、BCD、BCE、BDE、CDE.
解析答案
类型三 组合数公式及应用
角度1 有关组合数的计算与证明
反思与感悟
反思与感悟
解析答案
C
210
解析答案
角度2 含组合数的方程或不等式
即m2-23m+42=0
解得:m=2或21.
∵0≤m≤5,∴m=2,
解析答案
∴该不等式的解集为{6,7,8,9}.
反思与感悟
1.解答(1)易忽略根的检验而产生增根的错误,(2)易忽略n∈N*而导致错误.
2.与排列组合有关的方程或不等式问题要用到排列数、组合数公式,以及组合数的性质,求解时,要注意由 中的m∈N*,n∈N*,且n≥m确定m、n的范围,因此求解后要验证所得结果是否适合题意.
反思与感悟
所以(x-3)(x-6)=5×4×2=8×5.
所以x=11或x=-2(舍去负根).
经检验符合题意,所以方程的解为x=11.
解析答案
返回
解析答案
达标检测
1.下列问题中,组合问题的个数是( )
①从全班50人中选出5人组成班委会;②从全班50人中选出5人分别担任班长、副班长、团支部书记、学习委员、生活委员;③从1,2,3,…,9中任取出两个数求积;④从1,2,3,…,9中任取出两个数求差或商.
A.1 B.2 C.3 D.4
解析 对于①,从50人中选出5人组成班委会,不考虑顺序是组合问题.
②为排列问题.
对于③,从1,2,3,…,9中任取两个数求积是组合问题.
因为乘法满足交换律,而减法和除法不满足,故④为排列问题.
1
2
3
4
B
解析答案
解析 依题意,有x2-x=5x-5或x2-x+5x-5=16,解得x=1或5;
x=-7或x=3.
经检验知,只有x=1或x=3符合题意.
B
1
2
3
4
解析答案
解析 由题意知3≤n≤12,且n∈N*,
∴n=3,4,5,6,7.
D
1
2
3
4
4.下列等式不正确的是( )
D
答案
1
2
3
4
返回
规律与方法
1.排列与组合的联系与区别
(1)联系:二者都是从n个不同的元素中取m(m≤n)个元素.
(2)区别:排列问题中元素有序,组合问题中元素无序.
2.关于组合数的计算
