人教A版(2019)高中数学选择性必修第三册 6.2.2_排列数(共37张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 6.2.2_排列数(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 10:31:26 | ||
图片预览











文档简介
(共37张PPT)
6.2.2 排 列 数
1.进一步加深对排列概念的理解.
2.掌握几种有限制条件的排列,能应用排列数公式解决简单的实际问题.
问题导学
题型探究
达标检测
学习目标
问题导学 新知探究 点点落实
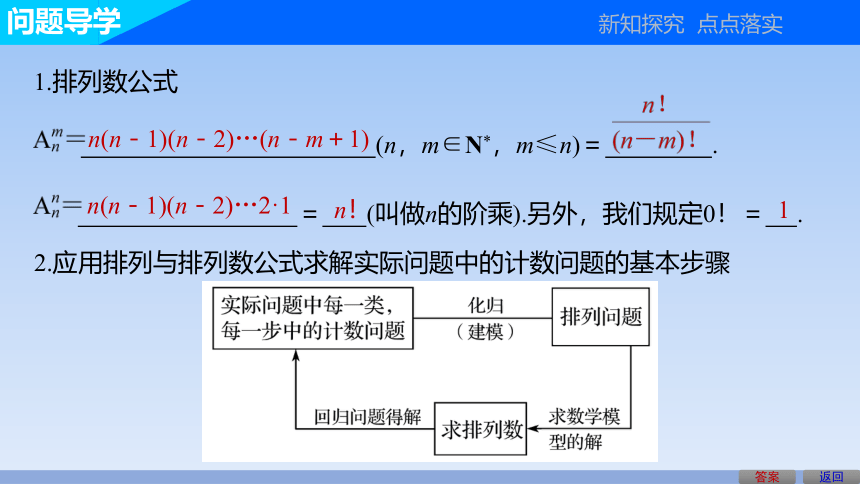
1.排列数公式
(n,m∈N*,m≤n)= .
n(n-1)(n-2)…(n-m+1)
= (叫做n的阶乘).另外,我们规定0!= .
2.应用排列与排列数公式求解实际问题中的计数问题的基本步骤
n!
1
n(n-1)(n-2)…2·1
答案
返回
类型一 无限制条件的排列问题
例1 (1)有7本不同的书,从中选3本送给3名同学,每人各1本,共有多少种不同的送法?
解 从7本不同的书中选3本送给3名同学,
相当于从7个元素中任取3个元素的一个排列,
解析答案
反思与感悟
题型探究 重点难点 个个击破
(2)有7种不同的书,要买3本送给3名同学,每人各1本,共有多少种不同的送法?
解 从7种不同的书中买3本书,这3本书并不要求都不相同,
根据分步乘法计数原理,共有不同的送法7×7×7=343(种).
反思与感悟
例1中两题的区别在于:(1)是典型的排列问题,用排列数计算其排列方法数;(2)不是排列问题,需用分步乘法计数原理求其方法种数.排列的概念很清楚,要从“n个不同的元素中取出m个元素”.即在排列问题中元素不能重复选取,而在用分步乘法计数原理解决的问题中.元素可以重复选取.
解析答案
跟踪训练1 (1)某信号兵用红、黄、蓝3面旗从上到下挂在竖直的旗杆上表示信号,每次可以任意挂1面、2面或3面,并且不同的顺序表示不同的信号,一共可以表示多少种不同的信号?
第二类用2面旗表示的信号有 种;
第三类用3面旗表示的信号有 种,
由分类加法计数原理,得所求的信号种数是:
即一共可以表示15种不同的信号.
解析答案
(2)将4名体育生,4名美术生分配到4个不同的班,每个班要分配一名体育生和一名美术生,共有多少种分配方案?
解 解决这类问题可以分为两步:
解析答案
类型二 排队问题
角度1 “相邻”与“不相邻”问题
例2 3名男生,4名女生,这7个人站成一排在下列情况下,各有多少种不同的站法.
(1)男、女各站在一起;
解 (相邻问题捆绑法)男生必须站在一起,
解析答案
(2)男生必须排在一起;
解 (捆绑法)把所有男生看作一个元素,与4名女生组成5个元素全排列,
(3)男生不能排在一起;
(4)男生互不相邻,且女生也互不相邻.
反思与感悟
反思与感悟
处理元素“相邻”“不相邻”问题应遵循“先整体,后局部”的原则.元素相邻问题,一般用“捆绑法”,先把相邻的若干个元素“捆绑”为一个大元素与其余元素全排列,然后再松绑,将这若干个元素内部全排列.元素不相邻问题,一般用“插空法”,先将不相邻元素以外的“普通”元素全排列,然后在“普通”元素之间及两端插入不相邻元素.
解析答案
跟踪训练2 排一张有5个歌唱节目和4个舞蹈节目的演出节目单.
(1)任何两个舞蹈节目不相邻的排法有多少种?
(2)歌唱节目与舞蹈节目间隔排列的方法有多少种?
解析答案
角度2 定序问题
例3 7人站成一排.
(1)甲必须在乙的前面(不一定相邻),则有多少种不同的排列方法;
解 甲在乙前面的排法种数占全体全排列种数的一半,
(2)甲、乙、丙三人自左向右的顺序不变(不一定相邻),则有多少不同的排列方法.
解 甲、乙、丙自左向右的顺序保持不变,
反思与感悟
反思与感悟
解析答案
跟踪训练3 7名师生排成一排照相,其中老师1人,女生2人,男生4人,若4名男生的身高都不等,按从高到低的顺序站,有多少种不同的站法?
而由高到低有从左到右和从右到左的不同站法,
解析答案
角度3 元素的“在”与“不在”问题
例4 从包括甲、乙两名同学在内的7名同学中选出5名同学排成一列,求解下列问题:
(1)甲不在首位的排法有多少种?
解 方法一 把同学作为研究对象.
第一类:不含甲,此时只需从甲以外的其他6名同学中取出5名放在5个位置上,有 种.
第二类:含有甲,甲不在首位:先从4个位置中选出1个放甲,
再从甲以外的6名同学中选出4名排在没有甲的位置上,
解析答案
方法二 把位置作为研究对象.
第二步,从占据首位以外的6名同学中选4名排在除首位以外的其他4个位置上,有 种方法.
方法三 (间接法):即先不考虑限制条件,从7名同学中选出5名进行排列,然后把不满足条件的排列去掉.
解析答案
(2)甲既不在首位,又不在末位的排法有多少种?
解 把位置作为研究对象,先满足特殊位置.
解析答案
(3)甲与乙既不在首位又不在末位的排法有多少种?
解 把位置作为研究对象.
解析答案
(4)甲不在首位,同时乙不在末位的排法有多少种?
解 用间接法.
注意到甲在首位同时乙在末位的情况被减去了两次,
反思与感悟
“在”与“不在”排列问题解题原则及方法
(1)原则:解“在”与“不在”的有限制条件的排列问题时,可以从元素入手也可以从位置入手,原则是谁特殊谁优先.
(2)方法:从元素入手时,先给特殊元素安排位置,再把其他元素安排在其他位置上,从位置入手时,先安排特殊位置,再安排其他位置.
提醒:解题时,或从元素考虑,或从位置考虑,都要贯彻到底.不能一会考虑元素,一会考虑位置,造成分类、分步混乱,导致解题错误.
反思与感悟
解析答案
跟踪训练4 7人站成一排,甲必须站在中间或两端,则有多少种不同站法?
解析答案
类型三 数字排列问题
例5 用0,1,2,3,4,5这六个数字可以组成多少个符合下列条件的无重复的数字?
(1)六位奇数;
解析答案
(2)个位数字不是5的六位数;
解 方法一 (直接法):
十万位数字的排法因个位上排0与不排0而有所不同,因此需分两类.
方法二 (排除法):
0在十万位和5在个位的排列都不对应符合题意的六位数,这两类排列中都含有0在十万位和5在个位的情况.
解析答案
(3)不大于4 310的四位偶数.
解 分三种情况,具体如下:
形如4 3××的只有4 310和4 302这两个数.
反思与感悟
数字排列问题是排列问题的重要题型,解题时要着重注意从附加受限制条件入手分析,找出解题的思路.常见附加条件有:(1)首位不能为0;(2)有无重复数字;(3)奇偶数;(4)某数的倍数;(5)大于(或小于)某数.
反思与感悟
解析答案
跟踪训练5 用0,1,2,3,4,5这六个数字可以组成多少个无重复数字的
(1)能被5整除的五位数;
解析答案
(2)能被3整除的五位数;
解 能被3整除的条件是各位数字之和能被3整徐,
则5个数可能有{1,2,3,4,5}和{0,1,2,4,5}两种情况,
(3)若所有的六位数按从小到大的顺序组成一个数列{an},则240 135是第几项.
解 由于是六位数,首位数字不能为0,
即240 135是数列的第193项.
解析答案
返回
解析答案
达标检测
1.用1,2,3,…,9这九个数字,可以组成没有重复数字的三位偶数的个数为( )
A.324 B.224 C.360 D.648
1
2
3
4
5
B
解析答案
2.6名学生排成两排,每排3人,则不同的排法种数为( )
A.36 B.120
C.720 D.240
解析 6个人站成两排,每排3人,
1
2
3
4
5
C
解析答案
3.从6名短跑运动员中选出4人参加4×100 m接力赛,甲不能跑第一棒和第四棒,问共有________种参赛方案.
1
2
3
4
5
解析 方法一 从人(元素)的角度考虑,优先考虑甲,分以下两类:
1
2
3
4
5
第2类,甲参赛,可优先将甲安排在第二棒或第三棒,有2种方法,
解析答案
方法二 从位置(元素)的角度考虑,优先考虑第一棒和第四棒,
1
2
3
4
5
由分步乘法计数原理可知,
方法三 (排除法):不考虑甲的约束,6个人占4个位置,
答案 240
解析答案
4.高二(一)班学生安排毕业晚会的4个音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求两个舞蹈节目不连排,则不同的排法的种数是______(填数字).
1
2
3
4
5
3 600
解析答案
5.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是____.
解析 将5张参观券分成4堆,有2个联号的有4种分法,
1
2
3
4
5
96
返回
规律与方法
求解排列问题的主要方法:
直接法 把符合条件的排列数直接列式计算
优先法 优先安排特殊元素或特殊位置
捆绑法 把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
插空法 对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空档中
定序问题 除法处理 对于定序问题,可先不考虑顺序限制,排列后,再除以定序元素的全排列
间接法 正难则反,等价转化的方法
6.2.2 排 列 数
1.进一步加深对排列概念的理解.
2.掌握几种有限制条件的排列,能应用排列数公式解决简单的实际问题.
问题导学
题型探究
达标检测
学习目标
问题导学 新知探究 点点落实
1.排列数公式
(n,m∈N*,m≤n)= .
n(n-1)(n-2)…(n-m+1)
= (叫做n的阶乘).另外,我们规定0!= .
2.应用排列与排列数公式求解实际问题中的计数问题的基本步骤
n!
1
n(n-1)(n-2)…2·1
答案
返回
类型一 无限制条件的排列问题
例1 (1)有7本不同的书,从中选3本送给3名同学,每人各1本,共有多少种不同的送法?
解 从7本不同的书中选3本送给3名同学,
相当于从7个元素中任取3个元素的一个排列,
解析答案
反思与感悟
题型探究 重点难点 个个击破
(2)有7种不同的书,要买3本送给3名同学,每人各1本,共有多少种不同的送法?
解 从7种不同的书中买3本书,这3本书并不要求都不相同,
根据分步乘法计数原理,共有不同的送法7×7×7=343(种).
反思与感悟
例1中两题的区别在于:(1)是典型的排列问题,用排列数计算其排列方法数;(2)不是排列问题,需用分步乘法计数原理求其方法种数.排列的概念很清楚,要从“n个不同的元素中取出m个元素”.即在排列问题中元素不能重复选取,而在用分步乘法计数原理解决的问题中.元素可以重复选取.
解析答案
跟踪训练1 (1)某信号兵用红、黄、蓝3面旗从上到下挂在竖直的旗杆上表示信号,每次可以任意挂1面、2面或3面,并且不同的顺序表示不同的信号,一共可以表示多少种不同的信号?
第二类用2面旗表示的信号有 种;
第三类用3面旗表示的信号有 种,
由分类加法计数原理,得所求的信号种数是:
即一共可以表示15种不同的信号.
解析答案
(2)将4名体育生,4名美术生分配到4个不同的班,每个班要分配一名体育生和一名美术生,共有多少种分配方案?
解 解决这类问题可以分为两步:
解析答案
类型二 排队问题
角度1 “相邻”与“不相邻”问题
例2 3名男生,4名女生,这7个人站成一排在下列情况下,各有多少种不同的站法.
(1)男、女各站在一起;
解 (相邻问题捆绑法)男生必须站在一起,
解析答案
(2)男生必须排在一起;
解 (捆绑法)把所有男生看作一个元素,与4名女生组成5个元素全排列,
(3)男生不能排在一起;
(4)男生互不相邻,且女生也互不相邻.
反思与感悟
反思与感悟
处理元素“相邻”“不相邻”问题应遵循“先整体,后局部”的原则.元素相邻问题,一般用“捆绑法”,先把相邻的若干个元素“捆绑”为一个大元素与其余元素全排列,然后再松绑,将这若干个元素内部全排列.元素不相邻问题,一般用“插空法”,先将不相邻元素以外的“普通”元素全排列,然后在“普通”元素之间及两端插入不相邻元素.
解析答案
跟踪训练2 排一张有5个歌唱节目和4个舞蹈节目的演出节目单.
(1)任何两个舞蹈节目不相邻的排法有多少种?
(2)歌唱节目与舞蹈节目间隔排列的方法有多少种?
解析答案
角度2 定序问题
例3 7人站成一排.
(1)甲必须在乙的前面(不一定相邻),则有多少种不同的排列方法;
解 甲在乙前面的排法种数占全体全排列种数的一半,
(2)甲、乙、丙三人自左向右的顺序不变(不一定相邻),则有多少不同的排列方法.
解 甲、乙、丙自左向右的顺序保持不变,
反思与感悟
反思与感悟
解析答案
跟踪训练3 7名师生排成一排照相,其中老师1人,女生2人,男生4人,若4名男生的身高都不等,按从高到低的顺序站,有多少种不同的站法?
而由高到低有从左到右和从右到左的不同站法,
解析答案
角度3 元素的“在”与“不在”问题
例4 从包括甲、乙两名同学在内的7名同学中选出5名同学排成一列,求解下列问题:
(1)甲不在首位的排法有多少种?
解 方法一 把同学作为研究对象.
第一类:不含甲,此时只需从甲以外的其他6名同学中取出5名放在5个位置上,有 种.
第二类:含有甲,甲不在首位:先从4个位置中选出1个放甲,
再从甲以外的6名同学中选出4名排在没有甲的位置上,
解析答案
方法二 把位置作为研究对象.
第二步,从占据首位以外的6名同学中选4名排在除首位以外的其他4个位置上,有 种方法.
方法三 (间接法):即先不考虑限制条件,从7名同学中选出5名进行排列,然后把不满足条件的排列去掉.
解析答案
(2)甲既不在首位,又不在末位的排法有多少种?
解 把位置作为研究对象,先满足特殊位置.
解析答案
(3)甲与乙既不在首位又不在末位的排法有多少种?
解 把位置作为研究对象.
解析答案
(4)甲不在首位,同时乙不在末位的排法有多少种?
解 用间接法.
注意到甲在首位同时乙在末位的情况被减去了两次,
反思与感悟
“在”与“不在”排列问题解题原则及方法
(1)原则:解“在”与“不在”的有限制条件的排列问题时,可以从元素入手也可以从位置入手,原则是谁特殊谁优先.
(2)方法:从元素入手时,先给特殊元素安排位置,再把其他元素安排在其他位置上,从位置入手时,先安排特殊位置,再安排其他位置.
提醒:解题时,或从元素考虑,或从位置考虑,都要贯彻到底.不能一会考虑元素,一会考虑位置,造成分类、分步混乱,导致解题错误.
反思与感悟
解析答案
跟踪训练4 7人站成一排,甲必须站在中间或两端,则有多少种不同站法?
解析答案
类型三 数字排列问题
例5 用0,1,2,3,4,5这六个数字可以组成多少个符合下列条件的无重复的数字?
(1)六位奇数;
解析答案
(2)个位数字不是5的六位数;
解 方法一 (直接法):
十万位数字的排法因个位上排0与不排0而有所不同,因此需分两类.
方法二 (排除法):
0在十万位和5在个位的排列都不对应符合题意的六位数,这两类排列中都含有0在十万位和5在个位的情况.
解析答案
(3)不大于4 310的四位偶数.
解 分三种情况,具体如下:
形如4 3××的只有4 310和4 302这两个数.
反思与感悟
数字排列问题是排列问题的重要题型,解题时要着重注意从附加受限制条件入手分析,找出解题的思路.常见附加条件有:(1)首位不能为0;(2)有无重复数字;(3)奇偶数;(4)某数的倍数;(5)大于(或小于)某数.
反思与感悟
解析答案
跟踪训练5 用0,1,2,3,4,5这六个数字可以组成多少个无重复数字的
(1)能被5整除的五位数;
解析答案
(2)能被3整除的五位数;
解 能被3整除的条件是各位数字之和能被3整徐,
则5个数可能有{1,2,3,4,5}和{0,1,2,4,5}两种情况,
(3)若所有的六位数按从小到大的顺序组成一个数列{an},则240 135是第几项.
解 由于是六位数,首位数字不能为0,
即240 135是数列的第193项.
解析答案
返回
解析答案
达标检测
1.用1,2,3,…,9这九个数字,可以组成没有重复数字的三位偶数的个数为( )
A.324 B.224 C.360 D.648
1
2
3
4
5
B
解析答案
2.6名学生排成两排,每排3人,则不同的排法种数为( )
A.36 B.120
C.720 D.240
解析 6个人站成两排,每排3人,
1
2
3
4
5
C
解析答案
3.从6名短跑运动员中选出4人参加4×100 m接力赛,甲不能跑第一棒和第四棒,问共有________种参赛方案.
1
2
3
4
5
解析 方法一 从人(元素)的角度考虑,优先考虑甲,分以下两类:
1
2
3
4
5
第2类,甲参赛,可优先将甲安排在第二棒或第三棒,有2种方法,
解析答案
方法二 从位置(元素)的角度考虑,优先考虑第一棒和第四棒,
1
2
3
4
5
由分步乘法计数原理可知,
方法三 (排除法):不考虑甲的约束,6个人占4个位置,
答案 240
解析答案
4.高二(一)班学生安排毕业晚会的4个音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求两个舞蹈节目不连排,则不同的排法的种数是______(填数字).
1
2
3
4
5
3 600
解析答案
5.将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是____.
解析 将5张参观券分成4堆,有2个联号的有4种分法,
1
2
3
4
5
96
返回
规律与方法
求解排列问题的主要方法:
直接法 把符合条件的排列数直接列式计算
优先法 优先安排特殊元素或特殊位置
捆绑法 把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
插空法 对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空档中
定序问题 除法处理 对于定序问题,可先不考虑顺序限制,排列后,再除以定序元素的全排列
间接法 正难则反,等价转化的方法
