人教A版(2019)高中数学选择性必修第三册 《排列》教学设计2
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 《排列》教学设计2 |
|
|
| 格式 | docx | ||
| 文件大小 | 279.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览


文档简介
《排列》教学设计
一、创设情境
(1)高二(1)班准备从甲、乙、丙3名学生中选出两人分别担任班长和副班长,共有多少种不同的选法
(2)从1,2,3这3个数字中,选出两个数字组成两位数,不同的两位数共有多少个
(3)北京、上海、广州3个民航站之间的直达航线,有多少种不同的飞机票
上面的三个问题有什么共同特征 可以用怎样的数学模型来分析
设计意图:这三个问题的实际背景不同,但去除实际背景之后,可抽象出共同的数学问题.教师引导学生用数学的眼光去看问题,用数学的思维去思考问题、分析问题、解决问题.
我们把上面问题中被取出的对象叫做元素.于是,所提出的问题就变为从3个不同的元素a,b,c中任意取出2个,然后按一定的顺序排成一列,求一共有多少种不同的排列方法.
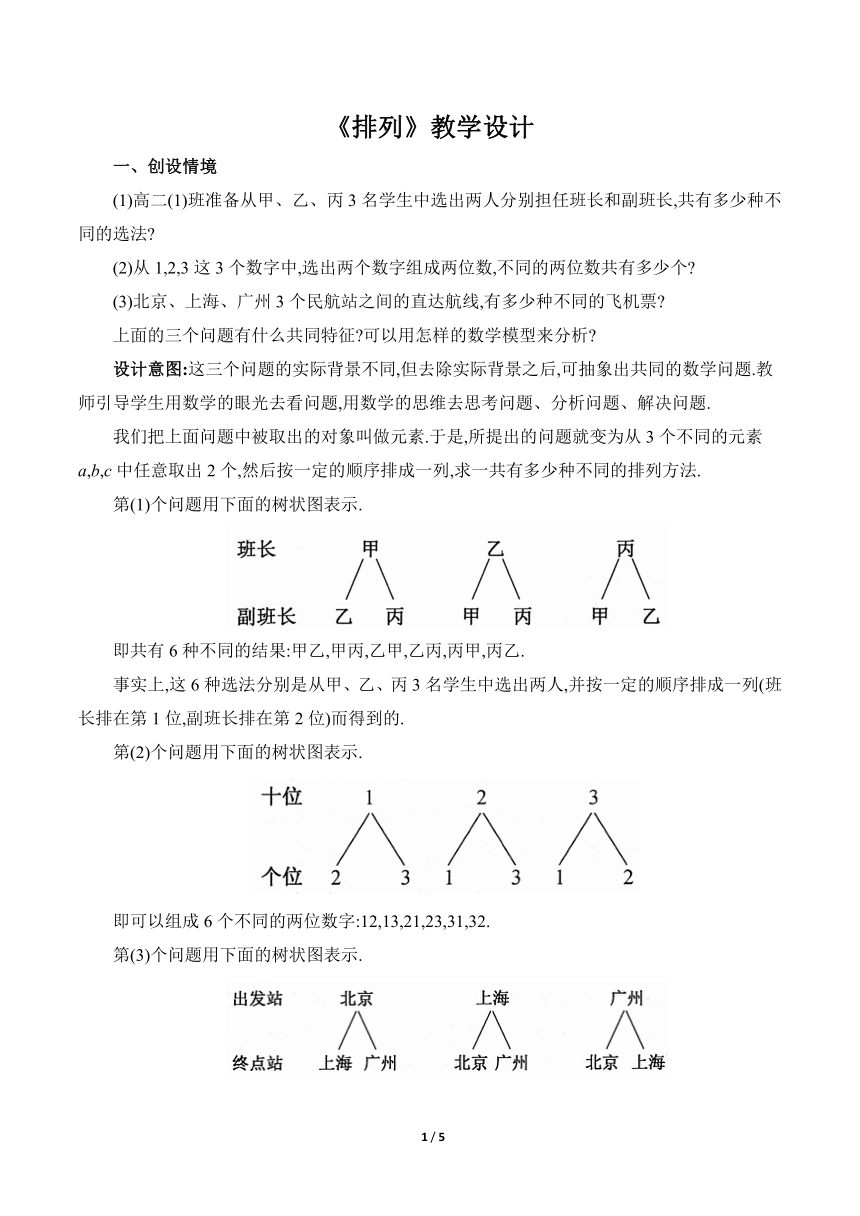
第(1)个问题用下面的树状图表示.
即共有6种不同的结果:甲乙,甲丙,乙甲,乙丙,丙甲,丙乙.
事实上,这6种选法分别是从甲、乙、丙3名学生中选出两人,并按一定的顺序排成一列(班长排在第1位,副班长排在第2位)而得到的.
第(2)个问题用下面的树状图表示.
即可以组成6个不同的两位数字:12,13,21,23,31,32.
第(3)个问题用下面的树状图表示.
即需要准备6种不同的飞机票:北京—上海,北京—广州,上海—北京,上海—广州,广州—北京,广州—上海.
设计意图:通过分析与解决以上三个问题,让学生感受这三个问题的数学本质是一样的,为引出排列的概念作准备.
二、形成概念,辨析概念
如果我们把上面问题中被取出的对象叫做元素,那么问题可叙述为:从3个不同的元素中任意取出2个,并按一定的顺序排成一列,共有多少种不同的排列方法
所有不同的排列是.
不同的排列方法种数是.
师生活动:
师生共同归纳出排列的定义:
一般地,从个不同元素中取出个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
判断下列问题是否是排列问题.
(1)从这4个数字中,任选2个做加法,其结果有多少种不同的可能
(2)从这4个数字中,任选2个做除法,其结果有多少种不同的可能
(3)从1到10这10个自然数中,任取2个组成点的坐标,可得到多少个不同的点的坐标
(4)平面上有5个点,任意三点不共线,这五点最多可确定多少条不同的直线 可确定多少条不同的射线
(5)10个学生排队照相,则不同的站法有多少种
师生活动:
教师展示问题,让学生思考分析,然后让学生展示思考分析的结果,检查学生对排列概念的理解.
学生回答:第(1)个问题不是排列问题;第(2)个问题是排列问题;第(3)个问题是排列问题;第(4)个问题不是排列问题;第(5)个问题是排列问题.
师生共同归纳总结:
排列的定义中包含两个基本内容:一是“取出元素”;二是“按照一定的顺序排成一列”.“一定的顺序”就是与位置有关,这也是判断一个问题是不是排列问题的重要标志.根据排列的定义,当且仅当两个排列的元素完全相同,而且元素的排列顺序也相同时,两个排列才相同.
设计意图:通过这5个问题,让学生进一步理解排列的概念.
三、应用举例,巩固概念
例1 某年全国足球甲级联赛共有14支队参加,每支队要与其余各队在主、客场分别比赛1场,共进行多少场比赛
师生活动:
师:你能用我们上一节学习的计数原理解决这一问题吗
生:要完成的“一件事情”是“从14支队中选出2支球队,按‘主队、客队’的顺序排成一个排列”.这里完成的“一件事情”与“顺序”有关,所以利用分步乘法计数原理可得,所以比赛的总场数是182.
师:根据我们这节课学的排列的概念,这是一个排列问题吗
生:是排列问题,相当于“从14个不同的元素中取出2个元素,并按照一定的顺序排成一列”.
例2 (1)从5本不同的书中选出3本送给3名同学,每人各1本,共有多少种不同的送法
(2)从5种不同的书中买3本送给3名同学,每人各1本,共有多少种不同的送法
师生活动:
师:这两个问题是否都是排列问题
学生思考、讨论、交流.
教师指名学生回答,根据学生的回答给出评价和指导.
师生共同得出结论:
这两个问题的区别在于:(1)是从5本不同的书中选出3本分别送给3名同学,每人得到的书不同,属于排列问题;而(2)中,由于不同的人得到的书的种类可能相同,因此不符合排列的概念,不是排列问题,只能用分步乘法计数原理求解.
教师指名学生回答问题
生1:(1)不同的送法种数为.
生2:(2)不同的送法种数为.
设计意图:通过对这两个问题的对比分析,让学生对排列的概念有更深刻的理解和认识,能在具体情境中识别是否是排列问题.
巩固练习:
(1)从参加乒乓球团体比赛的5名运动员中选出3名,并按一定的顺序出场比赛,有多少种不同的选法
(2)从4种蔬菜品种中选出3种,分别种植在不同土质的3块土地上,有多少种不同的种植方法
答案:
(1)从参加乒乓球团体比赛的5名运动员中选出3名,并按一定的顺序出场比赛,相当于从5个不同元素中取出3个元素,并按照一定的顺序排成一列,是一个排列问题,不同的选法种数为.
(2)从4种蔬菜品种中选出3种,分别种植在不同土质的3块土地上,相当于从4个不同元素中取出3个元素,并按照一定的顺序排成一列,是排列问题,所以不同的种植方法种数为.
四、课堂小结
1.排列问题实际上是一种特殊的计数问题,排列问题中要完成的“一件事情”包含两个基本步骤:一是“取出元素”;二是“按一定顺序排列”.
2.排列的定义是什么 如何利用排列的定义在具体的问题情境中识别是否是排列问题
3.两个排列相同的充要条件是什么
五、布置作业
教材第16~17页练习第1,2,3题.
板书设计:
6.2.1排列 一、创设情境 二、形成概念,辨析概念 1.排列的定义 一般地,从个不同元素中取出个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列. 2.两个排列相同的充要条件 两个排列相同的充要条件是两个排列的元素完全相同,且元素的排列顺序也相同 三、应用举例,巩固概念 例1 例2 四、课堂小结 五、布置作业
教学研讨:
本案例先创设三个具体的问题情境,这三个问题实际背景不同,有职务担任问题,有数字排列问题,还有飞机票的准备问题,但如果把这些问题去除实际背景,把“学生、数字、地点”都抽象成元素,就可得出共同的数学问题,把这类问题用数学的方法进行归纳,就得到了排列问题.引导学生用数学的眼光去看问题,用数学的思维去思考问题、分析问题、解决问题.然后通过两个具有实际情境的例题,让学生在具体情境中识别排列问题,加深对排列概念的理解与认识.教师可根据学生的情况,提供更加丰富的情境,也可让学生自己提供问题情境,师生共同分析,这样效果可能会更好.创造性地利用教材资源,合理运用教学方法,充分发挥多媒体教学的优势,为学生创设独立思考、自主探索、合作交流的学习环境,营造生动活泼的学习氛围,使学生充满信心、充满激情地学习.
1 / 5
一、创设情境
(1)高二(1)班准备从甲、乙、丙3名学生中选出两人分别担任班长和副班长,共有多少种不同的选法
(2)从1,2,3这3个数字中,选出两个数字组成两位数,不同的两位数共有多少个
(3)北京、上海、广州3个民航站之间的直达航线,有多少种不同的飞机票
上面的三个问题有什么共同特征 可以用怎样的数学模型来分析
设计意图:这三个问题的实际背景不同,但去除实际背景之后,可抽象出共同的数学问题.教师引导学生用数学的眼光去看问题,用数学的思维去思考问题、分析问题、解决问题.
我们把上面问题中被取出的对象叫做元素.于是,所提出的问题就变为从3个不同的元素a,b,c中任意取出2个,然后按一定的顺序排成一列,求一共有多少种不同的排列方法.
第(1)个问题用下面的树状图表示.
即共有6种不同的结果:甲乙,甲丙,乙甲,乙丙,丙甲,丙乙.
事实上,这6种选法分别是从甲、乙、丙3名学生中选出两人,并按一定的顺序排成一列(班长排在第1位,副班长排在第2位)而得到的.
第(2)个问题用下面的树状图表示.
即可以组成6个不同的两位数字:12,13,21,23,31,32.
第(3)个问题用下面的树状图表示.
即需要准备6种不同的飞机票:北京—上海,北京—广州,上海—北京,上海—广州,广州—北京,广州—上海.
设计意图:通过分析与解决以上三个问题,让学生感受这三个问题的数学本质是一样的,为引出排列的概念作准备.
二、形成概念,辨析概念
如果我们把上面问题中被取出的对象叫做元素,那么问题可叙述为:从3个不同的元素中任意取出2个,并按一定的顺序排成一列,共有多少种不同的排列方法
所有不同的排列是.
不同的排列方法种数是.
师生活动:
师生共同归纳出排列的定义:
一般地,从个不同元素中取出个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.
判断下列问题是否是排列问题.
(1)从这4个数字中,任选2个做加法,其结果有多少种不同的可能
(2)从这4个数字中,任选2个做除法,其结果有多少种不同的可能
(3)从1到10这10个自然数中,任取2个组成点的坐标,可得到多少个不同的点的坐标
(4)平面上有5个点,任意三点不共线,这五点最多可确定多少条不同的直线 可确定多少条不同的射线
(5)10个学生排队照相,则不同的站法有多少种
师生活动:
教师展示问题,让学生思考分析,然后让学生展示思考分析的结果,检查学生对排列概念的理解.
学生回答:第(1)个问题不是排列问题;第(2)个问题是排列问题;第(3)个问题是排列问题;第(4)个问题不是排列问题;第(5)个问题是排列问题.
师生共同归纳总结:
排列的定义中包含两个基本内容:一是“取出元素”;二是“按照一定的顺序排成一列”.“一定的顺序”就是与位置有关,这也是判断一个问题是不是排列问题的重要标志.根据排列的定义,当且仅当两个排列的元素完全相同,而且元素的排列顺序也相同时,两个排列才相同.
设计意图:通过这5个问题,让学生进一步理解排列的概念.
三、应用举例,巩固概念
例1 某年全国足球甲级联赛共有14支队参加,每支队要与其余各队在主、客场分别比赛1场,共进行多少场比赛
师生活动:
师:你能用我们上一节学习的计数原理解决这一问题吗
生:要完成的“一件事情”是“从14支队中选出2支球队,按‘主队、客队’的顺序排成一个排列”.这里完成的“一件事情”与“顺序”有关,所以利用分步乘法计数原理可得,所以比赛的总场数是182.
师:根据我们这节课学的排列的概念,这是一个排列问题吗
生:是排列问题,相当于“从14个不同的元素中取出2个元素,并按照一定的顺序排成一列”.
例2 (1)从5本不同的书中选出3本送给3名同学,每人各1本,共有多少种不同的送法
(2)从5种不同的书中买3本送给3名同学,每人各1本,共有多少种不同的送法
师生活动:
师:这两个问题是否都是排列问题
学生思考、讨论、交流.
教师指名学生回答,根据学生的回答给出评价和指导.
师生共同得出结论:
这两个问题的区别在于:(1)是从5本不同的书中选出3本分别送给3名同学,每人得到的书不同,属于排列问题;而(2)中,由于不同的人得到的书的种类可能相同,因此不符合排列的概念,不是排列问题,只能用分步乘法计数原理求解.
教师指名学生回答问题
生1:(1)不同的送法种数为.
生2:(2)不同的送法种数为.
设计意图:通过对这两个问题的对比分析,让学生对排列的概念有更深刻的理解和认识,能在具体情境中识别是否是排列问题.
巩固练习:
(1)从参加乒乓球团体比赛的5名运动员中选出3名,并按一定的顺序出场比赛,有多少种不同的选法
(2)从4种蔬菜品种中选出3种,分别种植在不同土质的3块土地上,有多少种不同的种植方法
答案:
(1)从参加乒乓球团体比赛的5名运动员中选出3名,并按一定的顺序出场比赛,相当于从5个不同元素中取出3个元素,并按照一定的顺序排成一列,是一个排列问题,不同的选法种数为.
(2)从4种蔬菜品种中选出3种,分别种植在不同土质的3块土地上,相当于从4个不同元素中取出3个元素,并按照一定的顺序排成一列,是排列问题,所以不同的种植方法种数为.
四、课堂小结
1.排列问题实际上是一种特殊的计数问题,排列问题中要完成的“一件事情”包含两个基本步骤:一是“取出元素”;二是“按一定顺序排列”.
2.排列的定义是什么 如何利用排列的定义在具体的问题情境中识别是否是排列问题
3.两个排列相同的充要条件是什么
五、布置作业
教材第16~17页练习第1,2,3题.
板书设计:
6.2.1排列 一、创设情境 二、形成概念,辨析概念 1.排列的定义 一般地,从个不同元素中取出个元素,并按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列. 2.两个排列相同的充要条件 两个排列相同的充要条件是两个排列的元素完全相同,且元素的排列顺序也相同 三、应用举例,巩固概念 例1 例2 四、课堂小结 五、布置作业
教学研讨:
本案例先创设三个具体的问题情境,这三个问题实际背景不同,有职务担任问题,有数字排列问题,还有飞机票的准备问题,但如果把这些问题去除实际背景,把“学生、数字、地点”都抽象成元素,就可得出共同的数学问题,把这类问题用数学的方法进行归纳,就得到了排列问题.引导学生用数学的眼光去看问题,用数学的思维去思考问题、分析问题、解决问题.然后通过两个具有实际情境的例题,让学生在具体情境中识别排列问题,加深对排列概念的理解与认识.教师可根据学生的情况,提供更加丰富的情境,也可让学生自己提供问题情境,师生共同分析,这样效果可能会更好.创造性地利用教材资源,合理运用教学方法,充分发挥多媒体教学的优势,为学生创设独立思考、自主探索、合作交流的学习环境,营造生动活泼的学习氛围,使学生充满信心、充满激情地学习.
1 / 5
