人教B版(2019)高中数学必修第一册 【整合精品课件】1.1.1《集合及其表示方法---第二课时集合的表示》(共37张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学必修第一册 【整合精品课件】1.1.1《集合及其表示方法---第二课时集合的表示》(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 701.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
1.1 集合
第一章 集合与常用逻辑用语
1.1.1 集合及其表示方法
第二课时 集合的表示
学习目标
1.通过实例,了解集合的含义,理解元素与集合的属于关系,
2.针对具体问题,能在自然语言、图形语言的基础上,用符号语言(列举法、描述法)刻画集合,
3.能正确使用区间符号表示某些集合.
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
集合的含义 数学抽象 水平1 水平1 1.理解并记住一些符号的含义,如,掌握常用数集的表示。 2.明确集合中元素的确定性、互异性,要特别注意“互异性”在解题中的应用。 3.学习的重点是集合的描述法,难点是由集合的描述法理解集合的含义。 【考查内容】集合的含义与表示是高考考查的热点,常考题型为新定义一个集合,求集合中元素的个数。
【考查题型】选择题
【分值情况】5分
元素与集合的关系 逻辑推理 水平1 水平2
常用数集的记法 数学抽象 水平1 水平1
集合的表示法 数学抽象 水平2 水平2
(1)把集合中的元素_________出来(相邻元素之间用 ____分隔),并写在______内,以此来表示集合的方法称为列举法.
知识点一 列举法
(一)教材梳理填空
一、自学教材·注重基础
(二)基本知能小试
1.判断正误
(1)由1,1,2,3组成的集合可用列举法表示为{1,1,2,3}. ( )
(2)0与{0}表示的是同一个集合. ( )
(3)方程(x-1)2·(x-2)=0的所有解的集合可表示为{1,2} . ( )
√
×
×
一、自学教材·注重基础
知识点一 列举法
3.设集合M={(1,2)},则下列关系式成立的是 ( )
A.1∈M B.2∈M C.(1,2)∈M D.(2,1)∈M
(二)基本知能小试
2.方程x2=4的解集用列举法表示为 ( )
A.{(-2,2)} B.{-2,2} C.{-2} D.{2}
解析:由x2=4得x=±2,故用列举法可表示为{-2,2}.
B
解析:共有1和-1两个元素.
C
一、自学教材·注重基础
知识点一 列举法
(一)教材梳理填空
知识点二 描述法
一、自学教材·注重基础
一般地,如果属于集合A的任意一个元素x都具有性质p(x),而不属于集合A的元素都不具有这个性质,则性质p(x)称为集合A的一个元素特征性质.此时,集合A可以用它的特征性质p(x)表示为_______.这种表示集合的方法,称为_________描述法,简称为描述法.
{x|p(x)}
特征性质
1.判断正误
(1)集合{x∈N|x>5}是用描述法表示的一个集合. ( )
(2)集合{x|4<x<5}是有限集. ( )
(3)集合A={x|x-1=0}与集合B={1}表示同一个集合. ( )
(二)基本知能小试
√
×
√
D
一、自学教材·注重基础
知识点二 描述法
2.集合A={x∈Z|-2<x<3}的元素个数为 ( )
A.1 B.2 C.3 D.4
解析:因为A={x∈Z|-2<x<3},所以x的取值为-1,0,1,2,共4个.
(二)基本知能小试
A
一、自学教材·注重基础
知识点二 描述法
3.已知集合A={x|x(x-2)=0},那么正确的是 ( )
A.0∈A B.2 A C.-1∈A D.0 A
解析:由x(x-2)=0得x=0或x=2,
∴A={0,2},∴0∈A.
(二)基本知能小试
①②④
一、自学教材·注重基础
知识点二 描述法
4.方程组的解集可表示为________(填序号).
①;②;
③{1,2};④{(x,y)|x=1,y=2}.
解析:原方程组的解为其解集中只含有一个元素,可表示为①②④.
(一)教材梳理填空
一、自学教材·注重基础
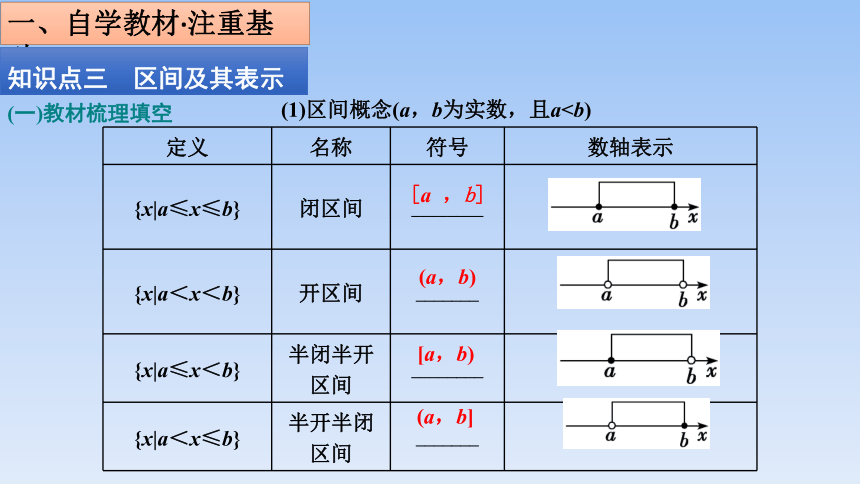
知识点三 区间及其表示
(1)区间概念(a,b为实数,且a定义 名称 符号 数轴表示
{x|a≤x≤b} 闭区间 ________
{x|a<x<b} 开区间 _______
{x|a≤x<b} 半闭半开区间 ________
{x|a<x≤b} 半开半闭区间 _______
[a ,b]
(a,b)
[a,b)
(a,b]
(一)教材梳理填空
一、自学教材·注重基础
知识点三 区间及其表示
(2)其它区间的表示
定义 R {x|x≥a} {x|x>a} {x|x≤a} {x|x符号 _____________ __________ __________ _________ _________
(-∞,+∞)
[a,+∞)
(a,+∞)
(-∞,a]
(-∞,a)
(二)基本知能小试
一、自学教材·注重基础
1.判断正误
(1)“∞”是一个符号,而不是一个数. ( )
(2)以“-∞”或“+∞”为端点时,区间这一端必须用小括号. ( )
(3)区间表示数集,数集一定能用区间表示. ( )
(4)数集{x|x≥2}可用区间表示为[2,+∞]. ( )
知识点三 区间及其表示
√
×
√
×
(二)基本知能小试
一、自学教材·注重基础
知识点三 区间及其表示
2.{x|-1≤x≤3}用区间表示为________.
3.{x|x<3}用区间表示为________.
4.若(2a,3a-1]为一确定的区间,则a的取值范围为________.
解析:由题意得3a-1>2a,∴a>1.
[-1,3]
(-∞,3)
{a|a>1}
题型一 列举法表示集合
列举法表示集合的种类
二、提升新知·注重综合
(1)元素个数少且有限时,如{1,2,3,4}.
(2)元素个数多且有限时,可以列举部分,中间用省略号表示.如“从1到100的所有自然数”可以表示为{1,2,3,4,…,100}.
(3)元素个数无限但有规律时,也可以类似地用省略号列举.如“所有的正偶数”可以表示为{2,4,6,8,…}.
题型一 列举法表示集合
二、提升新知·注重综合
例1、 用列举法表示下列给定的集合:
(1)不大于10的非负偶数组成的集合A;
(2)小于8的素数组成的集合B;
(3)方程x2-2x-3=0的实数根组成的集合C;
(4)方程组的解集D.
解析
(1)不大于10的非负偶数有0,2,4,6,8,10,所以A={0,2,4,6,8,10}.
(2)小于8的素数有2,3,5,7,所以B={2,3,5,7}.
题型一 列举法表示集合
二、提升新知·注重综合
例1、 用列举法表示下列给定的集合:
(1)不大于10的非负偶数组成的集合A;
(2)小于8的素数组成的集合B;
(3)方程x2-2x-3=0的实数根组成的集合C;
(4)方程组的解集D.
解析
(3)方程x2-2x-3=0的实数根为-1,3,所以C={-1,3}.
(4)方程组的解为所以方程组的解集D={(3,1)}.
题型一 列举法表示集合
二、提升新知·注重综合
方法总结
列举法表示集合的步骤及注意点
书写集合
分清元素
列元素时要做到不重复、不遗漏
列举法表示集合,要分清是数集还是点集
[提醒] 二元方程组的解集,函数的图像形成的集合都是点的集合,一定要写成实数对的形式,元素与元素之间用“,”隔开.如{(2,3),(5,-1)}.
变式训练
二、提升新知·注重综合
题型一 列举法表示集合
用列举法表示下列集合并判断它们是有限集还是无限集:
(1)一年中有31天的月份的全体;
(2)大于3.1小于12.8的整数的全体;
(3)方程+|y+1|=0的解集;
(4)正奇数组成的集合.
解析:(1){1月,3月,5月,7月,8月,10月,12月}.有限集.
(2){4,5,6,7,8,9,10,11,12}.有限集.
(3)由方程可知,
即
从而方程的解集用列举法表示为{(2,-1)}.有限集.
变式训练
二、提升新知·注重综合
题型一 列举法表示集合
用列举法表示下列集合并判断它们是有限集还是无限集:
(1)一年中有31天的月份的全体;
(2)大于3.1小于12.8的整数的全体;
(3)方程+|y+1|=0的解集;
(4)正奇数组成的集合.
解析:
(4)正奇数组成的集合可用列举法表示为{1,3,5,7,…}.无限集.
题型二 描述法表示集合
描述法表示集合的几点注意
二、提升新知·注重综合
(1)用描述法表示集合,应先弄清楚集合的属性,是数集、点集还是其他的类型.一般地,数集用一个字母代表其元素,而点集则用一个有序数对来表示其元素.
(2)用描述法表示集合时,若描述部分出现元素记号以外的字母,需对新字母说明其含义或取值范围.
(3)多层描述时,应当准确使用“且”和“或”,所有描述的内容都要写在集合内.
题型二 描述法表示集合
二、提升新知·注重综合
例2、 用描述法表示下列集合:
(1)不等式2x-3<1的解组成的集合A;
(2)被3除余2的正整数的集合B;
(3)C={2,4,6,8,10};
(4)平面直角坐标系中第二象限内的点组成的集合D.
解析
(1)不等式2x-3<1的解组成的集合为A,则集合A中的元素是数,设代表元素为x,则x满足2x-3<1,则A={x|2x-3<1},即A={x|x<2}.
(2)设被3除余2的数为x,则x=3n+2,n∈Z.但元素为正整数,故x=3n+2,n∈N.所以被3除余2的正整数的集合B={x|x=3n+2,n∈N}.
题型二 描述法表示集合
二、提升新知·注重综合
[典例2] 用描述法表示下列集合:
(1)不等式2x-3<1的解组成的集合A;
(2)被3除余2的正整数的集合B;
(3)C={2,4,6,8,10};
(4)平面直角坐标系中第二象限内的点组成的集合D.
解析
(3)设偶数为x,则x=2n,n∈Z.但元素是2,4,6,8,10,所以x=2n,n≤5,n∈N*.所以C={x|x=2n,n≤5,n∈N*}.
(4)平面直角坐标系中第二象限内的点的横坐标为负,纵坐标为正,即x<0,y>0,故第二象限内的点的集合为D={(x,y)|x<0,y>0}.
方法总结
二、提升新知·注重综合
题型二 描述法表示集合
1.描述法表示集合的2个步骤
方法总结
二、提升新知·注重综合
题型二 描述法表示集合
2.选用列举法或描述法的原则
要根据集合元素所具有的属性选择适当的表示方法.列举法的特点是能清楚地展现集合的元素,通常用于表示元素较少的集合,当集合中元素较多或无限时,就不宜采用列举法;描述法的特点是形式简单、应用方便,通常用于表示元素具有明显共同特征的集合,当元素共同特征不易寻找或元素的限制条件较多时,就不宜采用描述法.
变式训练
1.已知集合M={y|y=x2},用自然语言描述M应为 ( )
A.函数y=x2的值域
B.函数y=x2的定义域
C.函数y=x2的图像上的点组成的集合
D.以上说法都不对
解析:由于集合M={y|y=x2}的代表元素是y,而y为函数y=x2的函数值,则M为y=x2的值域.故A正确.函数y=x2的定义域是{x|y=x2},故B错误.函数y=x2的图像上的点组成的集合是{(x,y)|y=x2},故C错误.由于A对,故D错误.故选A.
A
二、提升新知·注重综合
题型二 描述法表示集合
变式训练
2.用符号“∈”或“ ”填空:
(1)A={x|x2-x=0},则1________A,-1________A;
(2)(1,2)________{(x,y)|y=x+1}.
解析:(1)易知A={0,1},故1∈A,-1 A;
(2)将x=1,y=2代入y=x+1,等式成立.
二、提升新知·注重综合
题型二 描述法表示集合
∈
∈
变式训练
3.用适当的方法表示下列集合:
(1)已知集合P={x|x=2n,0≤n≤2且n∈N};
(2)抛物线y=x2-2x与x轴的公共点的集合;
(3)直线y=x上去掉原点的点的集合.
解析: (1)列举法:P={0,2,4}.
(2)描述法: .
或列举法:{(0,0),(2,0)}.
(3)描述法:{(x,y)|y=x,x≠0}.
二、提升新知·注重综合
题型二 描述法表示集合
题型三 区间及其表示
区间是集合的又一种表示形式,对于区间的理解应注意:
(1)区间的左端点必须小于右端点,有时我们将b-a称为区间长度,对于只有一个元素的集合我们仍然用集合来表示,如{a}.
(2)注意开区间(a,b)与点(a,b)在具体情景中的区别.
(3)用数轴来表示区间时,要特别注意实心点与空心圈的区别.
(4)对于一个不等式的解集,我们既可以用集合形式来表示,也可以用区间形式来表示.
二、提升新知·注重综合
例3、把下列数集用区间表示:
(1){x|x≥-1};
(2){x|x<0};
(3){x|-1(4){x|-1(5){x|-2≤x<3}.
题型三 区间及其表示
解析
二、提升新知·注重综合
(1){x|x≥-1}=[-1,+∞).
(2){x|x<0}=(-∞,0).
(3){x|-1例3、把下列数集用区间表示:
(1){x|x≥-1};
(2){x|x<0};
(3){x|-1(4){x|-1(5){x|-2≤x<3}.
题型三 区间及其表示
解析
二、提升新知·注重综合
(4){x|-1(5){x|-2≤x<3}=[-2,3).
方法总结
二、提升新知·注重综合
题型三 区间及其表示
利用区间表示集合的三个原则
(1)连续的数集;(2)左端点必须小于右端点;(3)开或闭不能混淆.
[提醒] “∞”是一个趋向符号,表示无限接近,却永远不能到达,不是一个数.因此以“-∞”和“+∞”为区间的一端时,这一端点必须用小括号.
变式训练
1.不等式3x+1>0的解集可用区间表示为________.
解析:由3x+1>0,得.
2.使有意义的x的取值范围为_________.(用区间表示)
解析:由4-x>0,解得x<4,
所以x的取值范围为(-∞,4).
二、提升新知·注重综合
题型三 区间及其表示
(-∞,4)
当堂练习
1.把集合{x|x2-4x-5=0}用列举法表示为 ( )
A.{x=-1,x=5} B.{x|x=-1或x=5}
C.{x2-4x-5=0} D.{-1,5}
一、基础经典题
D
2.若集合A={(1,2),(3,4)},则集合A中元素的个数是 ( )
A.1 B.2 C.3 D.4
解析:集合A={(1,2),(3,4)}中有两个元素(1,2)和(3,4).
B
三、训练素养·注重应用、创新
当堂练习
3.设集合A={(x,y)|x+y=6,x∈N*,y∈N*},试问下列有序数对中,是集合A的元素的为 ( )
A.(1,5),(3,3),(2,4) B.(-1,7),(1,5),(4,2)
C.(0,6),(5,1),(3,3) D.(8,-2),(4,2),(3,3)
解析:A中符合题意;B中,-1 N*,故B不符合题意;C中0 N*,故C不符合题意;D中-2 N*,故D不符合题意.
A
三、训练素养·注重应用、创新
当堂练习
4.已知集合A={a+3,(a+1)2,a2+2a+2},若1∈A,则实数a的值为________.
解析:①若a+3=1,则a=-2,
此时A={1,1,2},不符合集合中元素的互异性,舍去.
②若(a+1)2=1,则a=0或a=-2.
当a=0时,A={3,1,2},满足题意;
当a=-2时,由①知不符合条件,故舍去.
③若a2+2a+2=1,则a=-1,
此时A={2,0,1},满足题意.
综上所述,实数a的值为-1或0.
-1或0
三、训练素养·注重应用、创新
当堂练习
5.定义P*Q={ab|a∈P,b∈Q},若P={0,1,2},Q={1,2,3},求P*Q中元素的个数.
解析:若a=0,则ab=0;若a=1,则ab=1,2,3;若a=2,则ab=2,4,6.故P*Q={0,1,2,3,4,6},共6个元素.
二、创新应用题
三、训练素养·注重应用、创新
1.1 集合
第一章 集合与常用逻辑用语
1.1.1 集合及其表示方法
第二课时 集合的表示
学习目标
1.通过实例,了解集合的含义,理解元素与集合的属于关系,
2.针对具体问题,能在自然语言、图形语言的基础上,用符号语言(列举法、描述法)刻画集合,
3.能正确使用区间符号表示某些集合.
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
集合的含义 数学抽象 水平1 水平1 1.理解并记住一些符号的含义,如,掌握常用数集的表示。 2.明确集合中元素的确定性、互异性,要特别注意“互异性”在解题中的应用。 3.学习的重点是集合的描述法,难点是由集合的描述法理解集合的含义。 【考查内容】集合的含义与表示是高考考查的热点,常考题型为新定义一个集合,求集合中元素的个数。
【考查题型】选择题
【分值情况】5分
元素与集合的关系 逻辑推理 水平1 水平2
常用数集的记法 数学抽象 水平1 水平1
集合的表示法 数学抽象 水平2 水平2
(1)把集合中的元素_________出来(相邻元素之间用 ____分隔),并写在______内,以此来表示集合的方法称为列举法.
知识点一 列举法
(一)教材梳理填空
一、自学教材·注重基础
(二)基本知能小试
1.判断正误
(1)由1,1,2,3组成的集合可用列举法表示为{1,1,2,3}. ( )
(2)0与{0}表示的是同一个集合. ( )
(3)方程(x-1)2·(x-2)=0的所有解的集合可表示为{1,2} . ( )
√
×
×
一、自学教材·注重基础
知识点一 列举法
3.设集合M={(1,2)},则下列关系式成立的是 ( )
A.1∈M B.2∈M C.(1,2)∈M D.(2,1)∈M
(二)基本知能小试
2.方程x2=4的解集用列举法表示为 ( )
A.{(-2,2)} B.{-2,2} C.{-2} D.{2}
解析:由x2=4得x=±2,故用列举法可表示为{-2,2}.
B
解析:共有1和-1两个元素.
C
一、自学教材·注重基础
知识点一 列举法
(一)教材梳理填空
知识点二 描述法
一、自学教材·注重基础
一般地,如果属于集合A的任意一个元素x都具有性质p(x),而不属于集合A的元素都不具有这个性质,则性质p(x)称为集合A的一个元素特征性质.此时,集合A可以用它的特征性质p(x)表示为_______.这种表示集合的方法,称为_________描述法,简称为描述法.
{x|p(x)}
特征性质
1.判断正误
(1)集合{x∈N|x>5}是用描述法表示的一个集合. ( )
(2)集合{x|4<x<5}是有限集. ( )
(3)集合A={x|x-1=0}与集合B={1}表示同一个集合. ( )
(二)基本知能小试
√
×
√
D
一、自学教材·注重基础
知识点二 描述法
2.集合A={x∈Z|-2<x<3}的元素个数为 ( )
A.1 B.2 C.3 D.4
解析:因为A={x∈Z|-2<x<3},所以x的取值为-1,0,1,2,共4个.
(二)基本知能小试
A
一、自学教材·注重基础
知识点二 描述法
3.已知集合A={x|x(x-2)=0},那么正确的是 ( )
A.0∈A B.2 A C.-1∈A D.0 A
解析:由x(x-2)=0得x=0或x=2,
∴A={0,2},∴0∈A.
(二)基本知能小试
①②④
一、自学教材·注重基础
知识点二 描述法
4.方程组的解集可表示为________(填序号).
①;②;
③{1,2};④{(x,y)|x=1,y=2}.
解析:原方程组的解为其解集中只含有一个元素,可表示为①②④.
(一)教材梳理填空
一、自学教材·注重基础
知识点三 区间及其表示
(1)区间概念(a,b为实数,且a
{x|a≤x≤b} 闭区间 ________
{x|a<x<b} 开区间 _______
{x|a≤x<b} 半闭半开区间 ________
{x|a<x≤b} 半开半闭区间 _______
[a ,b]
(a,b)
[a,b)
(a,b]
(一)教材梳理填空
一、自学教材·注重基础
知识点三 区间及其表示
(2)其它区间的表示
定义 R {x|x≥a} {x|x>a} {x|x≤a} {x|x
(-∞,+∞)
[a,+∞)
(a,+∞)
(-∞,a]
(-∞,a)
(二)基本知能小试
一、自学教材·注重基础
1.判断正误
(1)“∞”是一个符号,而不是一个数. ( )
(2)以“-∞”或“+∞”为端点时,区间这一端必须用小括号. ( )
(3)区间表示数集,数集一定能用区间表示. ( )
(4)数集{x|x≥2}可用区间表示为[2,+∞]. ( )
知识点三 区间及其表示
√
×
√
×
(二)基本知能小试
一、自学教材·注重基础
知识点三 区间及其表示
2.{x|-1≤x≤3}用区间表示为________.
3.{x|x<3}用区间表示为________.
4.若(2a,3a-1]为一确定的区间,则a的取值范围为________.
解析:由题意得3a-1>2a,∴a>1.
[-1,3]
(-∞,3)
{a|a>1}
题型一 列举法表示集合
列举法表示集合的种类
二、提升新知·注重综合
(1)元素个数少且有限时,如{1,2,3,4}.
(2)元素个数多且有限时,可以列举部分,中间用省略号表示.如“从1到100的所有自然数”可以表示为{1,2,3,4,…,100}.
(3)元素个数无限但有规律时,也可以类似地用省略号列举.如“所有的正偶数”可以表示为{2,4,6,8,…}.
题型一 列举法表示集合
二、提升新知·注重综合
例1、 用列举法表示下列给定的集合:
(1)不大于10的非负偶数组成的集合A;
(2)小于8的素数组成的集合B;
(3)方程x2-2x-3=0的实数根组成的集合C;
(4)方程组的解集D.
解析
(1)不大于10的非负偶数有0,2,4,6,8,10,所以A={0,2,4,6,8,10}.
(2)小于8的素数有2,3,5,7,所以B={2,3,5,7}.
题型一 列举法表示集合
二、提升新知·注重综合
例1、 用列举法表示下列给定的集合:
(1)不大于10的非负偶数组成的集合A;
(2)小于8的素数组成的集合B;
(3)方程x2-2x-3=0的实数根组成的集合C;
(4)方程组的解集D.
解析
(3)方程x2-2x-3=0的实数根为-1,3,所以C={-1,3}.
(4)方程组的解为所以方程组的解集D={(3,1)}.
题型一 列举法表示集合
二、提升新知·注重综合
方法总结
列举法表示集合的步骤及注意点
书写集合
分清元素
列元素时要做到不重复、不遗漏
列举法表示集合,要分清是数集还是点集
[提醒] 二元方程组的解集,函数的图像形成的集合都是点的集合,一定要写成实数对的形式,元素与元素之间用“,”隔开.如{(2,3),(5,-1)}.
变式训练
二、提升新知·注重综合
题型一 列举法表示集合
用列举法表示下列集合并判断它们是有限集还是无限集:
(1)一年中有31天的月份的全体;
(2)大于3.1小于12.8的整数的全体;
(3)方程+|y+1|=0的解集;
(4)正奇数组成的集合.
解析:(1){1月,3月,5月,7月,8月,10月,12月}.有限集.
(2){4,5,6,7,8,9,10,11,12}.有限集.
(3)由方程可知,
即
从而方程的解集用列举法表示为{(2,-1)}.有限集.
变式训练
二、提升新知·注重综合
题型一 列举法表示集合
用列举法表示下列集合并判断它们是有限集还是无限集:
(1)一年中有31天的月份的全体;
(2)大于3.1小于12.8的整数的全体;
(3)方程+|y+1|=0的解集;
(4)正奇数组成的集合.
解析:
(4)正奇数组成的集合可用列举法表示为{1,3,5,7,…}.无限集.
题型二 描述法表示集合
描述法表示集合的几点注意
二、提升新知·注重综合
(1)用描述法表示集合,应先弄清楚集合的属性,是数集、点集还是其他的类型.一般地,数集用一个字母代表其元素,而点集则用一个有序数对来表示其元素.
(2)用描述法表示集合时,若描述部分出现元素记号以外的字母,需对新字母说明其含义或取值范围.
(3)多层描述时,应当准确使用“且”和“或”,所有描述的内容都要写在集合内.
题型二 描述法表示集合
二、提升新知·注重综合
例2、 用描述法表示下列集合:
(1)不等式2x-3<1的解组成的集合A;
(2)被3除余2的正整数的集合B;
(3)C={2,4,6,8,10};
(4)平面直角坐标系中第二象限内的点组成的集合D.
解析
(1)不等式2x-3<1的解组成的集合为A,则集合A中的元素是数,设代表元素为x,则x满足2x-3<1,则A={x|2x-3<1},即A={x|x<2}.
(2)设被3除余2的数为x,则x=3n+2,n∈Z.但元素为正整数,故x=3n+2,n∈N.所以被3除余2的正整数的集合B={x|x=3n+2,n∈N}.
题型二 描述法表示集合
二、提升新知·注重综合
[典例2] 用描述法表示下列集合:
(1)不等式2x-3<1的解组成的集合A;
(2)被3除余2的正整数的集合B;
(3)C={2,4,6,8,10};
(4)平面直角坐标系中第二象限内的点组成的集合D.
解析
(3)设偶数为x,则x=2n,n∈Z.但元素是2,4,6,8,10,所以x=2n,n≤5,n∈N*.所以C={x|x=2n,n≤5,n∈N*}.
(4)平面直角坐标系中第二象限内的点的横坐标为负,纵坐标为正,即x<0,y>0,故第二象限内的点的集合为D={(x,y)|x<0,y>0}.
方法总结
二、提升新知·注重综合
题型二 描述法表示集合
1.描述法表示集合的2个步骤
方法总结
二、提升新知·注重综合
题型二 描述法表示集合
2.选用列举法或描述法的原则
要根据集合元素所具有的属性选择适当的表示方法.列举法的特点是能清楚地展现集合的元素,通常用于表示元素较少的集合,当集合中元素较多或无限时,就不宜采用列举法;描述法的特点是形式简单、应用方便,通常用于表示元素具有明显共同特征的集合,当元素共同特征不易寻找或元素的限制条件较多时,就不宜采用描述法.
变式训练
1.已知集合M={y|y=x2},用自然语言描述M应为 ( )
A.函数y=x2的值域
B.函数y=x2的定义域
C.函数y=x2的图像上的点组成的集合
D.以上说法都不对
解析:由于集合M={y|y=x2}的代表元素是y,而y为函数y=x2的函数值,则M为y=x2的值域.故A正确.函数y=x2的定义域是{x|y=x2},故B错误.函数y=x2的图像上的点组成的集合是{(x,y)|y=x2},故C错误.由于A对,故D错误.故选A.
A
二、提升新知·注重综合
题型二 描述法表示集合
变式训练
2.用符号“∈”或“ ”填空:
(1)A={x|x2-x=0},则1________A,-1________A;
(2)(1,2)________{(x,y)|y=x+1}.
解析:(1)易知A={0,1},故1∈A,-1 A;
(2)将x=1,y=2代入y=x+1,等式成立.
二、提升新知·注重综合
题型二 描述法表示集合
∈
∈
变式训练
3.用适当的方法表示下列集合:
(1)已知集合P={x|x=2n,0≤n≤2且n∈N};
(2)抛物线y=x2-2x与x轴的公共点的集合;
(3)直线y=x上去掉原点的点的集合.
解析: (1)列举法:P={0,2,4}.
(2)描述法: .
或列举法:{(0,0),(2,0)}.
(3)描述法:{(x,y)|y=x,x≠0}.
二、提升新知·注重综合
题型二 描述法表示集合
题型三 区间及其表示
区间是集合的又一种表示形式,对于区间的理解应注意:
(1)区间的左端点必须小于右端点,有时我们将b-a称为区间长度,对于只有一个元素的集合我们仍然用集合来表示,如{a}.
(2)注意开区间(a,b)与点(a,b)在具体情景中的区别.
(3)用数轴来表示区间时,要特别注意实心点与空心圈的区别.
(4)对于一个不等式的解集,我们既可以用集合形式来表示,也可以用区间形式来表示.
二、提升新知·注重综合
例3、把下列数集用区间表示:
(1){x|x≥-1};
(2){x|x<0};
(3){x|-1
题型三 区间及其表示
解析
二、提升新知·注重综合
(1){x|x≥-1}=[-1,+∞).
(2){x|x<0}=(-∞,0).
(3){x|-1
(1){x|x≥-1};
(2){x|x<0};
(3){x|-1
题型三 区间及其表示
解析
二、提升新知·注重综合
(4){x|-1
方法总结
二、提升新知·注重综合
题型三 区间及其表示
利用区间表示集合的三个原则
(1)连续的数集;(2)左端点必须小于右端点;(3)开或闭不能混淆.
[提醒] “∞”是一个趋向符号,表示无限接近,却永远不能到达,不是一个数.因此以“-∞”和“+∞”为区间的一端时,这一端点必须用小括号.
变式训练
1.不等式3x+1>0的解集可用区间表示为________.
解析:由3x+1>0,得.
2.使有意义的x的取值范围为_________.(用区间表示)
解析:由4-x>0,解得x<4,
所以x的取值范围为(-∞,4).
二、提升新知·注重综合
题型三 区间及其表示
(-∞,4)
当堂练习
1.把集合{x|x2-4x-5=0}用列举法表示为 ( )
A.{x=-1,x=5} B.{x|x=-1或x=5}
C.{x2-4x-5=0} D.{-1,5}
一、基础经典题
D
2.若集合A={(1,2),(3,4)},则集合A中元素的个数是 ( )
A.1 B.2 C.3 D.4
解析:集合A={(1,2),(3,4)}中有两个元素(1,2)和(3,4).
B
三、训练素养·注重应用、创新
当堂练习
3.设集合A={(x,y)|x+y=6,x∈N*,y∈N*},试问下列有序数对中,是集合A的元素的为 ( )
A.(1,5),(3,3),(2,4) B.(-1,7),(1,5),(4,2)
C.(0,6),(5,1),(3,3) D.(8,-2),(4,2),(3,3)
解析:A中符合题意;B中,-1 N*,故B不符合题意;C中0 N*,故C不符合题意;D中-2 N*,故D不符合题意.
A
三、训练素养·注重应用、创新
当堂练习
4.已知集合A={a+3,(a+1)2,a2+2a+2},若1∈A,则实数a的值为________.
解析:①若a+3=1,则a=-2,
此时A={1,1,2},不符合集合中元素的互异性,舍去.
②若(a+1)2=1,则a=0或a=-2.
当a=0时,A={3,1,2},满足题意;
当a=-2时,由①知不符合条件,故舍去.
③若a2+2a+2=1,则a=-1,
此时A={2,0,1},满足题意.
综上所述,实数a的值为-1或0.
-1或0
三、训练素养·注重应用、创新
当堂练习
5.定义P*Q={ab|a∈P,b∈Q},若P={0,1,2},Q={1,2,3},求P*Q中元素的个数.
解析:若a=0,则ab=0;若a=1,则ab=1,2,3;若a=2,则ab=2,4,6.故P*Q={0,1,2,3,4,6},共6个元素.
二、创新应用题
三、训练素养·注重应用、创新
