人教B版(2019)高中数学必修第一册 【整合精品课件】1.1.1《集合及其表示方法---第一课时集合的含义》(共25张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学必修第一册 【整合精品课件】1.1.1《集合及其表示方法---第一课时集合的含义》(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 615.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
1.1 集合
第一章 集合与常用逻辑用语
1.1.1 集合及其表示方法
第一课时 集合的含义
学习目标
1.通过实例,了解集合的含义,理解元素与集合的属于关系,
2.针对具体问题,能在自然语言、图形语言的基础上,用符号语言(列举法、描述法)刻画集合,
3.能正确使用区间符号表示某些集合.
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
集合的含义 数学抽象 水平1 水平1 1.理解并记住一些符号的含义,如,掌握常用数集的表示。 2.明确集合中元素的确定性、互异性,要特别注意“互异性”在解题中的应用。 3.学习的重点是集合的描述法,难点是由集合的描述法理解集合的含义。 【考查内容】集合的含义与表示是高考考查的热点,常考题型为新定义一个集合,求集合中元素的个数。
【考查题型】选择题
【分值情况】5分
元素与集合的关系 逻辑推理 水平1 水平2
常用数集的记法 数学抽象 水平1 水平1
集合的表示法 数学抽象 水平2 水平2
(1)集合:把一些能够 的、 的对象汇集在一起,就说由这些对象组成一个集合(有时简称为___).
(3)集合与元素的记法:集合通常用英文大写字母A,B,C,…表示,元素通常用英文 小写字母a,b,c…表示.
知识点一 集合与元素
(2)元素:组成集合的 都是这个集合的元素.
(一)教材梳理填空
一、自学教材·注重基础
关系 语言描述 记法 读法
属于 a是集合A的元素 ______ a属于A
不属于 a不是集合A的元素 ______ a不属于A
a∈A
a A
(4)元素与集合的关系
知识点一 集合与元素
(一)教材梳理填空
(5)空集
一般地,我们把 的集合称为空集,记作____.
不含任何元素
一、自学教材·注重基础
(7)两集合相等
给定两个集合A和B,如果组成它们的元素 ,就称这两个集合相等.记作A=B.
(6)集合的元素特点
①确定性:集合的元素必须是 的.
②互异性:对于一个给定的集合,集合中的元素一定是 的.
③无序性:集合中的元素可以任意 .
确定
排列
不同
完全相同
(8)集合的分类
集合可以根据它含有的元素个数分为两类:
①有限集:含有 元素的集合.
②无限集:含有 元素的集合.
有限个
无限个
一、自学教材·注重基础
知识点一 集合与元素
(二)基本知能小试
1.判断正误
(1)你班所有的姓氏能组成集合. ( )
(2)数学课本上的所有难题能组成集合. ( )
(3)一个集合中可以找到两个相同的元素. ( )
(4)空集中只有元素0,而无其余元素. ( )
(5)空集是有限集. ( )
√
√
×
×
×
一、自学教材·注重基础
3.方程x2-1=0与方程x+1=0所有解组成的集合中共有_____个元素.
知识点一 集合与元素
(二)基本知能小试
2.已知集合A由x<1的数构成,则有 ( )
A.3∈A B.1∈A C.0∈A D.-1 A
解析:很明显3,1不满足不等式,而0,-1满足不等式.
C
解析:共有1和-1两个元素.
2
4.已知集合A含有三个元素0,1,x-2,则实数x不能取的值是____.
解析:由集合元素的互异性知, x-2≠0,且x-2≠1,故x≠2,且x≠3.
2,3
5.已知集合A中有三个元素1,a2,2,B中有三个元素1,4,a,且集合A与集合B相等,则a=________.
解析:∵A=B,∴a2=4且a=2,解得a=2.
2
一、自学教材·注重基础
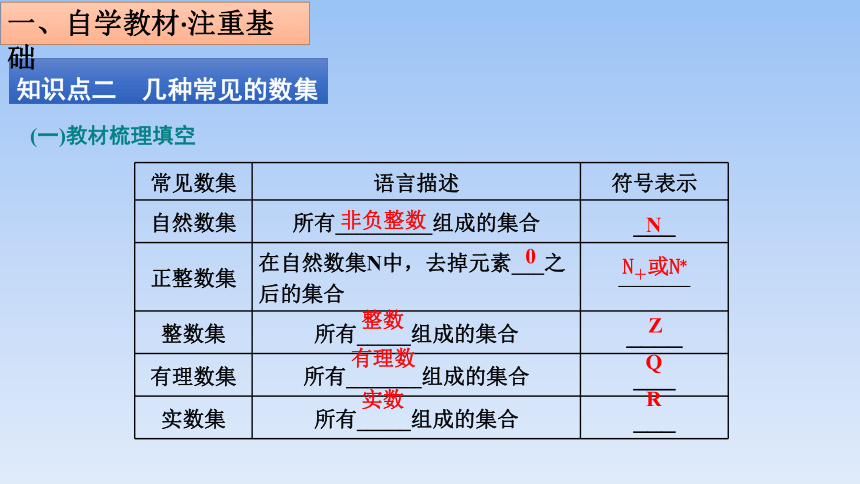
常见数集 语言描述 符号表示
自然数集 所有_________组成的集合 ___
正整数集 在自然数集N中,去掉元素___之后的集合 ________
整数集 所有_____组成的集合 ____
有理数集 所有_______组成的集合 ___
实数集 所有_____组成的集合 ___
非负整数
N
Z
Q
R
整数
有理数
实数
0
N+或N*
(一)教材梳理填空
知识点二 几种常见的数集
一、自学教材·注重基础
知识点二 几种常见的数集
1.判断正误
(1)集合N与集合N+是同一个集合. ( )
(2)集合N中的元素都是集合Z中的元素. ( )
(3)集合Q中的元素都是集合Z中的元素. ( )
(4)集合Q中的元素都是集合R中的元素. ( )
(二)基本知能小试
×
√
×
√
A
A
一、自学教材·注重基础
广泛性
整体性
描述性
组成集合的对象可以是数、点、图形、多项式、方程,也可以是人或物等
集合是一个整体,暗含“所有”“全部”“全体”的含义,因此一些对象一旦组成了集合,这个集合就是这些对象的总体
“集合”是一个原始的不加定义的概念,它同平面几何中的“点”“线”“面”等概念一样都只是描述性的说明
题型一 集合的概念
三方面理解集合的含义
不是所有的对象都能构成集合,只有具有明确标准可以判定是否在集合内的对象才能组成集合.
二、提升新知·注重综合
题型一 集合的概念
例1、考查下列每组对象,能构成一个集合的是( )
①某校高一年级成绩优秀的学生;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④2018年第23届冬季奥运会金牌获得者.
A.③④ B.②③④ C.②③ D.②④
①中“成绩优秀”没有明确的标准,所以不能构成一个集合;②③④中的对象都满足确定性,所以能构成集合.
B
解析
二、提升新知·注重综合
变式训练
1.现有以下说法:
①高二(1)班较胖的同学构成一个集合;
②正方体的全体构成一个集合;
③未来世界的高科技产品构成一个集合;
④不大于3的所有自然数构成一个集合.
其中正确的是 ( )
A.①② B.②③ C.③④ D.②④
题型一 集合的概念
解析:在①中,高二(1)班较胖的同学不能构成一个集合,故①错误;在②中,正方体的全体能构成一个集合,故②正确;在③中,未来世界的高科技产品不能构成一个集合,故③错误;在④中,不大于3的所有自然数能构成一个集合,故④正确.
D
二、提升新知·注重综合
变式训练
题型一 集合的概念
2.判断下列每组对象能否组成一个集合.
(1)参加2018年俄罗斯世界杯足球赛的所有国家;
(2)参加2018年俄罗斯世界杯足球赛的所有实力较强的球队;
(3)参加2018年五四青年节联欢晚会的所有同学;
(4)直角坐标系中接近原点的点.
解:(1)中“所有国家”,(3)中“所有同学”,都有确定的“属性”,能组成集合.
(2)中“实力较强的球队”,没有明确的标准,(4)中“接近原点”,界限不明,都不能组成集合.
综上可知,(1)(3)能组成集合,(2)(4)不能组成集合.
二、提升新知·注重综合
方向性
唯一性
符号“∈”“ ”具有方向性,左边是元素,右边是集合
a∈A与a A取决于a是不是集合A中的元素,只有属于和不属于两种关系
题型二 元素与集合的关系
元素与集合的关系解读
二、提升新知·注重综合
题型二 元素与集合的关系
(2)由题意可得:3-x可以为1,2,3,6,且x为自然数,因此x的值为2,1,0.因此A中元素有2,1,0.
解析
B
2,1,0
二、提升新知·注重综合
例2、 (1)下列所给关系正确的个数是 ( )
①π∈R;② Q;③0∈N*;④|-5| N*.
A.1 B.2 C.3 D.4
(2)集合A中的元素x满足∈N,x∈N,则集合A中的元素为________.
(1)①π是实数,所以π∈R正确;② 是无理数,所以 Q正确;③0不是正整数,所以0∈N*错误;④|-5|=5为正整数,所以|-5| N*错误.故选B.
推理法
直接法
(2)判断方法:首先明确已知集合的元素具有什么特征,然后判断该元素是否满足集合中元素所具有的特征即可
(1)使用前提:对于某些不便直接表示的集合
(1)使用前提:集合中的元素是直接给出的
(2)判断方法:首先明确集合是由哪些元素构成,然后再判断该元素在已知集合中是否出现即可
题型二 元素与集合的关系
判断元素与集合关系的两种方法
方法总结
二、提升新知·注重综合
变式训练
题型二 元素与集合的关系
1.已知集合A中元素满足2x+a>0,a∈R,若1 A,2∈A,则 ( )
A.a>-4 B.a≤-2 C.-4<a<-2 D.-4<a≤-2
解析:∵1 A,2∈A,∴2×1+ a ≤0,且2×2+ a >0,解得-4< a ≤-2.
D
2.用符号“∈”或“ ”填空.
(1)设集合M中的元素为平行四边形,p表示某个矩形,q表示某个梯形,则p ____M,q____ M.
(2)设集合D是满足方程y=x2的有序数对(x,y)的集合,则-1_____D,(-1,1)____D.
解析:(1)矩形是平行四边形,梯形不是平行四边形,故p∈M,q M.
(2)因为集合D中的元素是有序数对(x,y),而-1是数,所以-1 D,(-1,1)∈D.
∈
二、提升新知·注重综合
∈
例3、已知集合A含有两个元素a-3和2a-1,若-3∈A,试求实数a的值.
题型三 集合中元素特性的简单应用
因为-3∈A,
所以-3=a-3或-3=2a-1.
若-3=a-3,则a=0.
此时集合A含有两个元素-3和-1,符合要求;
若-3=2a-1,则a=-1,
此时,集合A含有两个元素-4,-3,符合要求.
综上所述,满足题意的实数a的值为0或-1.
解析
二、提升新知·注重综合
根据集合中元素的特性求值的3个步骤
题型三 集合中元素特性的简单应用
方法总结
二、提升新知·注重综合
题型三 集合中元素特性的简单应用
变式训练
1.[已知元素与集合的关系求参数]已知集合A中有0,m,m2-3m+2三个元素,且2∈A,则实数m为 ( )
A.2 B.3 C.0或3 D.0,2,3均可
解析:由2∈A可知:若m=2,则m2-3m+2=0,这与m2-3m+2≠0相矛盾;若m2-3m+2=2,则m=0或m=3,当m=0时,与m≠0相矛盾,当m=3时,此时集合A中含有3个元素0,2,3,故选B.
B
A
2.[判断集合中元素的个数]由实数x,-x,|x|, 及所组成的集合,最多含有 ( )
A.2个元素 B.3个元素 C.4个元素 D.5个元素
解析:法一:因为|x|=±x, =|x|,= x,所以不论x取何值,最多只能写成两种形式:x,-x,故集合中最多含有2个元素.
法二:令x=2,则以上实数分别为:2, 2,2,2, 2,由元素互异性知集合最多含有2个元素.
二、提升新知·注重综合
题型三 集合中元素特性的简单应用
变式训练
3.[由集合元素特征求参数]设集合A中有两个元素x,y,B中有两个元素0,x2,若A与B的元素相同,则实数x的值为________,y的值为________.
解析:因为集合A,B的元素相同,所以x=0或y=0.
①当x=0时,x2=0,则B中有两个元素0,不满足集合中元素的互异性,故舍去;
②当y=0时,x=x2,解得x=0或x=1,由①知x=0应舍去,故x=1.
综上可知,x=1,y=0.
1 0
二、提升新知·注重综合
当堂练习
1.若以集合A的四个元素a,b,c,d为边长构成一个四边形,则这个四边形可能是 ( )
A.梯形 B.平行四边形 C.菱形 D.矩形
一、基础经典题
解析:由于a,b,c,d四个元素互不相同,故它们组成的四边形的四条边都不相等.
A
2.下列各组对象能构成集合的有 ( )
①接近于1的所有正整数;②小于0的实数;
③(2 019,1)与(1,2 019).
A.1组 B.2组 C.3组 D.0组
解析:①中接近于1的所有正整数标准不明确,故不能构成集合;②中“小于0”是一个明确的标准,能构成集合;③中(2 019,1)与(1,2 019)是两个不同的数对,是确定的,能构成集合.
B
三、训练素养·注重应用、创新
当堂练习
3.“booknote”中的字母构成一个集合,该集合的元素个数是________.
解析:根据集合元素的互异性可知,booknote中的不同字母共有“b,o,k,n,t,e”6个,故该集合的元素个数是6.
4.给出下列说法:
①中国的所有直辖市可以构成一个集合;
②高一(1)班较高的同学可以构成一个集合;
③正偶数的全体可以构成一个集合;
④大于2 013且小于2 019的所有整数不能构成集合.
其中正确的有________.(填序号)
解析:②中由于“较高”的标准不明确,不满足集合元素的确定性,所以②错误;④中的所有整数能构成集合,所以④错误.
①③
6
三、训练素养·注重应用、创新
当堂练习
5.已知集合A中含有三个元素a-3,2a-1,a2-4,且-3∈A,求实数a的值.
解析:(1)若a-3=-3,则a=0,此时A中元素分别为-3,-1,-4,满足题意.
(2)若2a-1=-3,则a=-1,此时A中元素分别为-4,-3,-3,不满足元素的互异性.
(3)若a2-4=-3,则a=±1.
当a=1时,A中的元素分别为-2,1,-3,满足题意;
当a=-1时,由(2)知不合题意.
综上可知,a=0或a=1.
二、创新应用题
三、训练素养·注重应用、创新
1.1 集合
第一章 集合与常用逻辑用语
1.1.1 集合及其表示方法
第一课时 集合的含义
学习目标
1.通过实例,了解集合的含义,理解元素与集合的属于关系,
2.针对具体问题,能在自然语言、图形语言的基础上,用符号语言(列举法、描述法)刻画集合,
3.能正确使用区间符号表示某些集合.
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
集合的含义 数学抽象 水平1 水平1 1.理解并记住一些符号的含义,如,掌握常用数集的表示。 2.明确集合中元素的确定性、互异性,要特别注意“互异性”在解题中的应用。 3.学习的重点是集合的描述法,难点是由集合的描述法理解集合的含义。 【考查内容】集合的含义与表示是高考考查的热点,常考题型为新定义一个集合,求集合中元素的个数。
【考查题型】选择题
【分值情况】5分
元素与集合的关系 逻辑推理 水平1 水平2
常用数集的记法 数学抽象 水平1 水平1
集合的表示法 数学抽象 水平2 水平2
(1)集合:把一些能够 的、 的对象汇集在一起,就说由这些对象组成一个集合(有时简称为___).
(3)集合与元素的记法:集合通常用英文大写字母A,B,C,…表示,元素通常用英文 小写字母a,b,c…表示.
知识点一 集合与元素
(2)元素:组成集合的 都是这个集合的元素.
(一)教材梳理填空
一、自学教材·注重基础
关系 语言描述 记法 读法
属于 a是集合A的元素 ______ a属于A
不属于 a不是集合A的元素 ______ a不属于A
a∈A
a A
(4)元素与集合的关系
知识点一 集合与元素
(一)教材梳理填空
(5)空集
一般地,我们把 的集合称为空集,记作____.
不含任何元素
一、自学教材·注重基础
(7)两集合相等
给定两个集合A和B,如果组成它们的元素 ,就称这两个集合相等.记作A=B.
(6)集合的元素特点
①确定性:集合的元素必须是 的.
②互异性:对于一个给定的集合,集合中的元素一定是 的.
③无序性:集合中的元素可以任意 .
确定
排列
不同
完全相同
(8)集合的分类
集合可以根据它含有的元素个数分为两类:
①有限集:含有 元素的集合.
②无限集:含有 元素的集合.
有限个
无限个
一、自学教材·注重基础
知识点一 集合与元素
(二)基本知能小试
1.判断正误
(1)你班所有的姓氏能组成集合. ( )
(2)数学课本上的所有难题能组成集合. ( )
(3)一个集合中可以找到两个相同的元素. ( )
(4)空集中只有元素0,而无其余元素. ( )
(5)空集是有限集. ( )
√
√
×
×
×
一、自学教材·注重基础
3.方程x2-1=0与方程x+1=0所有解组成的集合中共有_____个元素.
知识点一 集合与元素
(二)基本知能小试
2.已知集合A由x<1的数构成,则有 ( )
A.3∈A B.1∈A C.0∈A D.-1 A
解析:很明显3,1不满足不等式,而0,-1满足不等式.
C
解析:共有1和-1两个元素.
2
4.已知集合A含有三个元素0,1,x-2,则实数x不能取的值是____.
解析:由集合元素的互异性知, x-2≠0,且x-2≠1,故x≠2,且x≠3.
2,3
5.已知集合A中有三个元素1,a2,2,B中有三个元素1,4,a,且集合A与集合B相等,则a=________.
解析:∵A=B,∴a2=4且a=2,解得a=2.
2
一、自学教材·注重基础
常见数集 语言描述 符号表示
自然数集 所有_________组成的集合 ___
正整数集 在自然数集N中,去掉元素___之后的集合 ________
整数集 所有_____组成的集合 ____
有理数集 所有_______组成的集合 ___
实数集 所有_____组成的集合 ___
非负整数
N
Z
Q
R
整数
有理数
实数
0
N+或N*
(一)教材梳理填空
知识点二 几种常见的数集
一、自学教材·注重基础
知识点二 几种常见的数集
1.判断正误
(1)集合N与集合N+是同一个集合. ( )
(2)集合N中的元素都是集合Z中的元素. ( )
(3)集合Q中的元素都是集合Z中的元素. ( )
(4)集合Q中的元素都是集合R中的元素. ( )
(二)基本知能小试
×
√
×
√
A
A
一、自学教材·注重基础
广泛性
整体性
描述性
组成集合的对象可以是数、点、图形、多项式、方程,也可以是人或物等
集合是一个整体,暗含“所有”“全部”“全体”的含义,因此一些对象一旦组成了集合,这个集合就是这些对象的总体
“集合”是一个原始的不加定义的概念,它同平面几何中的“点”“线”“面”等概念一样都只是描述性的说明
题型一 集合的概念
三方面理解集合的含义
不是所有的对象都能构成集合,只有具有明确标准可以判定是否在集合内的对象才能组成集合.
二、提升新知·注重综合
题型一 集合的概念
例1、考查下列每组对象,能构成一个集合的是( )
①某校高一年级成绩优秀的学生;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④2018年第23届冬季奥运会金牌获得者.
A.③④ B.②③④ C.②③ D.②④
①中“成绩优秀”没有明确的标准,所以不能构成一个集合;②③④中的对象都满足确定性,所以能构成集合.
B
解析
二、提升新知·注重综合
变式训练
1.现有以下说法:
①高二(1)班较胖的同学构成一个集合;
②正方体的全体构成一个集合;
③未来世界的高科技产品构成一个集合;
④不大于3的所有自然数构成一个集合.
其中正确的是 ( )
A.①② B.②③ C.③④ D.②④
题型一 集合的概念
解析:在①中,高二(1)班较胖的同学不能构成一个集合,故①错误;在②中,正方体的全体能构成一个集合,故②正确;在③中,未来世界的高科技产品不能构成一个集合,故③错误;在④中,不大于3的所有自然数能构成一个集合,故④正确.
D
二、提升新知·注重综合
变式训练
题型一 集合的概念
2.判断下列每组对象能否组成一个集合.
(1)参加2018年俄罗斯世界杯足球赛的所有国家;
(2)参加2018年俄罗斯世界杯足球赛的所有实力较强的球队;
(3)参加2018年五四青年节联欢晚会的所有同学;
(4)直角坐标系中接近原点的点.
解:(1)中“所有国家”,(3)中“所有同学”,都有确定的“属性”,能组成集合.
(2)中“实力较强的球队”,没有明确的标准,(4)中“接近原点”,界限不明,都不能组成集合.
综上可知,(1)(3)能组成集合,(2)(4)不能组成集合.
二、提升新知·注重综合
方向性
唯一性
符号“∈”“ ”具有方向性,左边是元素,右边是集合
a∈A与a A取决于a是不是集合A中的元素,只有属于和不属于两种关系
题型二 元素与集合的关系
元素与集合的关系解读
二、提升新知·注重综合
题型二 元素与集合的关系
(2)由题意可得:3-x可以为1,2,3,6,且x为自然数,因此x的值为2,1,0.因此A中元素有2,1,0.
解析
B
2,1,0
二、提升新知·注重综合
例2、 (1)下列所给关系正确的个数是 ( )
①π∈R;② Q;③0∈N*;④|-5| N*.
A.1 B.2 C.3 D.4
(2)集合A中的元素x满足∈N,x∈N,则集合A中的元素为________.
(1)①π是实数,所以π∈R正确;② 是无理数,所以 Q正确;③0不是正整数,所以0∈N*错误;④|-5|=5为正整数,所以|-5| N*错误.故选B.
推理法
直接法
(2)判断方法:首先明确已知集合的元素具有什么特征,然后判断该元素是否满足集合中元素所具有的特征即可
(1)使用前提:对于某些不便直接表示的集合
(1)使用前提:集合中的元素是直接给出的
(2)判断方法:首先明确集合是由哪些元素构成,然后再判断该元素在已知集合中是否出现即可
题型二 元素与集合的关系
判断元素与集合关系的两种方法
方法总结
二、提升新知·注重综合
变式训练
题型二 元素与集合的关系
1.已知集合A中元素满足2x+a>0,a∈R,若1 A,2∈A,则 ( )
A.a>-4 B.a≤-2 C.-4<a<-2 D.-4<a≤-2
解析:∵1 A,2∈A,∴2×1+ a ≤0,且2×2+ a >0,解得-4< a ≤-2.
D
2.用符号“∈”或“ ”填空.
(1)设集合M中的元素为平行四边形,p表示某个矩形,q表示某个梯形,则p ____M,q____ M.
(2)设集合D是满足方程y=x2的有序数对(x,y)的集合,则-1_____D,(-1,1)____D.
解析:(1)矩形是平行四边形,梯形不是平行四边形,故p∈M,q M.
(2)因为集合D中的元素是有序数对(x,y),而-1是数,所以-1 D,(-1,1)∈D.
∈
二、提升新知·注重综合
∈
例3、已知集合A含有两个元素a-3和2a-1,若-3∈A,试求实数a的值.
题型三 集合中元素特性的简单应用
因为-3∈A,
所以-3=a-3或-3=2a-1.
若-3=a-3,则a=0.
此时集合A含有两个元素-3和-1,符合要求;
若-3=2a-1,则a=-1,
此时,集合A含有两个元素-4,-3,符合要求.
综上所述,满足题意的实数a的值为0或-1.
解析
二、提升新知·注重综合
根据集合中元素的特性求值的3个步骤
题型三 集合中元素特性的简单应用
方法总结
二、提升新知·注重综合
题型三 集合中元素特性的简单应用
变式训练
1.[已知元素与集合的关系求参数]已知集合A中有0,m,m2-3m+2三个元素,且2∈A,则实数m为 ( )
A.2 B.3 C.0或3 D.0,2,3均可
解析:由2∈A可知:若m=2,则m2-3m+2=0,这与m2-3m+2≠0相矛盾;若m2-3m+2=2,则m=0或m=3,当m=0时,与m≠0相矛盾,当m=3时,此时集合A中含有3个元素0,2,3,故选B.
B
A
2.[判断集合中元素的个数]由实数x,-x,|x|, 及所组成的集合,最多含有 ( )
A.2个元素 B.3个元素 C.4个元素 D.5个元素
解析:法一:因为|x|=±x, =|x|,= x,所以不论x取何值,最多只能写成两种形式:x,-x,故集合中最多含有2个元素.
法二:令x=2,则以上实数分别为:2, 2,2,2, 2,由元素互异性知集合最多含有2个元素.
二、提升新知·注重综合
题型三 集合中元素特性的简单应用
变式训练
3.[由集合元素特征求参数]设集合A中有两个元素x,y,B中有两个元素0,x2,若A与B的元素相同,则实数x的值为________,y的值为________.
解析:因为集合A,B的元素相同,所以x=0或y=0.
①当x=0时,x2=0,则B中有两个元素0,不满足集合中元素的互异性,故舍去;
②当y=0时,x=x2,解得x=0或x=1,由①知x=0应舍去,故x=1.
综上可知,x=1,y=0.
1 0
二、提升新知·注重综合
当堂练习
1.若以集合A的四个元素a,b,c,d为边长构成一个四边形,则这个四边形可能是 ( )
A.梯形 B.平行四边形 C.菱形 D.矩形
一、基础经典题
解析:由于a,b,c,d四个元素互不相同,故它们组成的四边形的四条边都不相等.
A
2.下列各组对象能构成集合的有 ( )
①接近于1的所有正整数;②小于0的实数;
③(2 019,1)与(1,2 019).
A.1组 B.2组 C.3组 D.0组
解析:①中接近于1的所有正整数标准不明确,故不能构成集合;②中“小于0”是一个明确的标准,能构成集合;③中(2 019,1)与(1,2 019)是两个不同的数对,是确定的,能构成集合.
B
三、训练素养·注重应用、创新
当堂练习
3.“booknote”中的字母构成一个集合,该集合的元素个数是________.
解析:根据集合元素的互异性可知,booknote中的不同字母共有“b,o,k,n,t,e”6个,故该集合的元素个数是6.
4.给出下列说法:
①中国的所有直辖市可以构成一个集合;
②高一(1)班较高的同学可以构成一个集合;
③正偶数的全体可以构成一个集合;
④大于2 013且小于2 019的所有整数不能构成集合.
其中正确的有________.(填序号)
解析:②中由于“较高”的标准不明确,不满足集合元素的确定性,所以②错误;④中的所有整数能构成集合,所以④错误.
①③
6
三、训练素养·注重应用、创新
当堂练习
5.已知集合A中含有三个元素a-3,2a-1,a2-4,且-3∈A,求实数a的值.
解析:(1)若a-3=-3,则a=0,此时A中元素分别为-3,-1,-4,满足题意.
(2)若2a-1=-3,则a=-1,此时A中元素分别为-4,-3,-3,不满足元素的互异性.
(3)若a2-4=-3,则a=±1.
当a=1时,A中的元素分别为-2,1,-3,满足题意;
当a=-1时,由(2)知不合题意.
综上可知,a=0或a=1.
二、创新应用题
三、训练素养·注重应用、创新
