人教B版(2019)高中数学必修第一册1.1 《集合及其表示方法》教学设计(表格式)
文档属性
| 名称 | 人教B版(2019)高中数学必修第一册1.1 《集合及其表示方法》教学设计(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 199.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 10:49:49 | ||
图片预览


文档简介
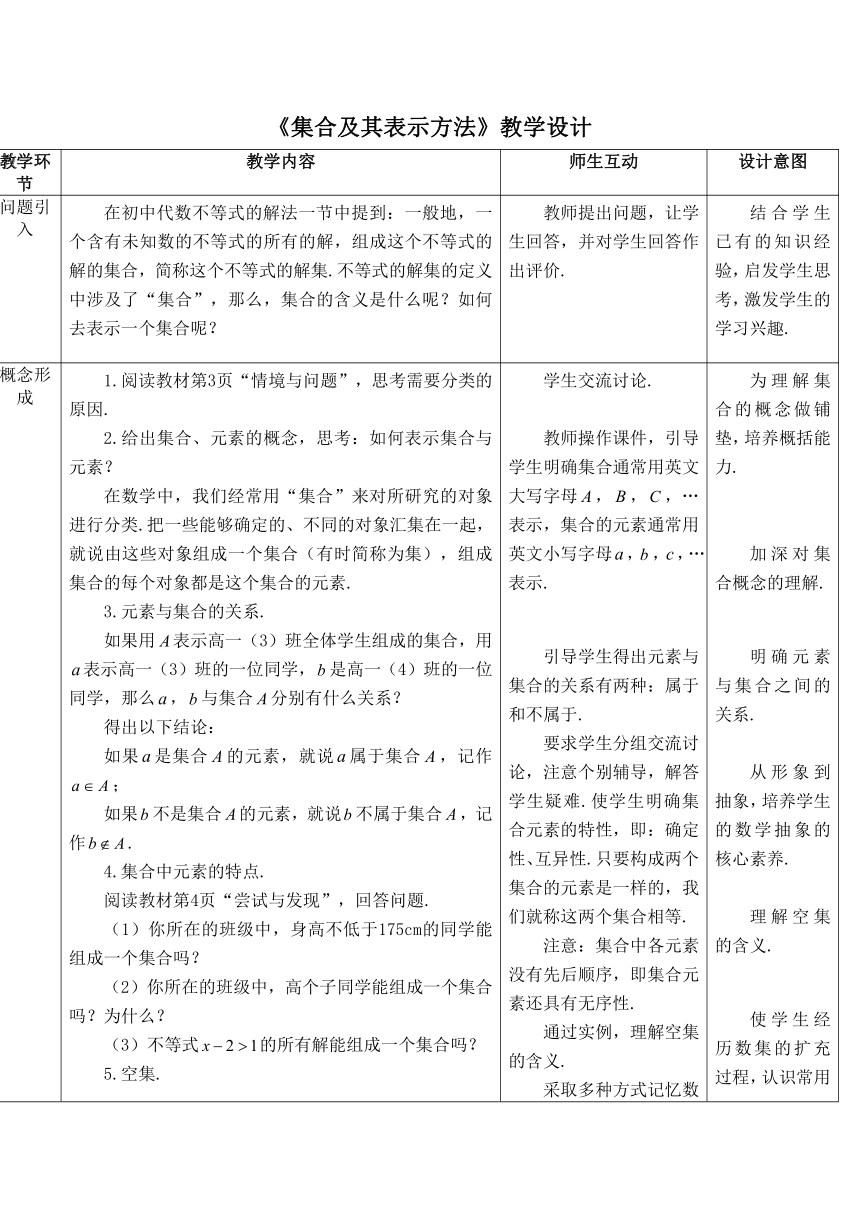
《集合及其表示方法》教学设计
教学环节 教学内容 师生互动 设计意图
问题引入 在初中代数不等式的解法一节中提到:一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称这个不等式的解集.不等式的解集的定义中涉及了“集合”,那么,集合的含义是什么呢?如何去表示一个集合呢? 教师提出问题,让学生回答,并对学生回答作出评价. 结合学生已有的知识经验,启发学生思考,激发学生的学习兴趣.
概念形成 1.阅读教材第3页“情境与问题”,思考需要分类的原因. 2.给出集合、元素的概念,思考:如何表示集合与元素? 在数学中,我们经常用“集合”来对所研究的对象进行分类.把一些能够确定的、不同的对象汇集在一起,就说由这些对象组成一个集合(有时简称为集),组成集合的每个对象都是这个集合的元素. 3.元素与集合的关系. 如果用表示高一(3)班全体学生组成的集合,用表示高一(3)班的一位同学,是高一(4)班的一位同学,那么,与集合分别有什么关系? 得出以下结论: 如果是集合的元素,就说属于集合,记作; 如果不是集合的元素,就说不属于集合,记作. 4.集合中元素的特点. 阅读教材第4页“尝试与发现”,回答问题. (1)你所在的班级中,身高不低于175cm的同学能组成一个集合吗? (2)你所在的班级中,高个子同学能组成一个集合吗?为什么? (3)不等式的所有解能组成一个集合吗? 5.空集. 不含任何元素的集合称为空集,记作. 6.几个常见的数集. 阅读教材第4~5页内容,认识常见数集的符号表示,回答“想一想”的问题. 常见数集的专用符号. :非负整数集(或自然数集)(全体非负整数的集合); 或:正整数集(非负整数集内排除0的集合); :整数集(全体整数的集合); :有理数集(全体有理数的集合); :实数集(全体实数的集合). 想一想: (1)无限循环小数可以表示成分数吗? (2)任何一个无限循环小数都是中的元素,这种说法正确吗? 7.集合的分类. 集合分类的标准是什么? 集合可以根据它含有的元素个数分为两类:含有有限个元素的集合称为有限集,含有无限个元素的集合称为无限集.空集可以看成包含0个元素的集合,所以空集是有限集. 8.集合的表示. 阅读教材中的相关内容,并思考、讨论下列问题: (1)要表示一个集合共有几种方式? (2)试比较自然语言、列举法和描述法在表示集合时,各自有什么特点?适用的对象分别是什么? (3)如何根据问题选择适当的集合表示方法? 9.区间. (1)一般区间的表示. 设,,且,规定如下: 定义名称符号数轴表示闭区间开区间半开半闭区间半开半闭区间
(2)特殊区间的表示. 定义符号
学生交流讨论. 教师操作课件,引导学生明确集合通常用英文大写字母,,,…表示,集合的元素通常用英文小写字母,,,…表示. 引导学生得出元素与集合的关系有两种:属于和不属于. 要求学生分组交流讨论,注意个别辅导,解答学生疑难.使学生明确集合元素的特性,即:确定性、互异性.只要构成两个集合的元素是一样的,我们就称这两个集合相等. 注意:集合中各元素没有先后顺序,即集合元素还具有无序性. 通过实例,理解空集的含义. 采取多种方式记忆数集的符号,引导学生规范使用符号. 通过实例,引导学生根据集合中元素的个数对集合进行分类. 要求学生掌握表示集合的两种方法:列举法和描述法,多举一些例子,多练习. 组织学生将一些数集表示为区间,进一步熟练掌握集合与区间的应用. 为理解集合的概念做铺垫,培养概括能力. 加深对集合概念的理解. 明确元素与集合之间的关系. 从形象到抽象,培养学生的数学抽象的核心素养. 理解空集的含义. 使学生经历数集的扩充过程,认识常用数集的符号. 体会有限集、无限集的概念. 使学生弄清楚集合表示方法的优缺点,体会它们存在的必要性和适用对象. 体会集合与区间的联系与区别.
概念深化 1.关于集合的元素的特征的理解. (1)确定性:设是一个给定的集合,是某一个具体对象,则或者是的元素,或者不是的元素,两种情况必有一种且只有一种成立. (2)互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素.相同的对象归入同一个集合时只能算作集合中的一个元素. (3)无序性:集合中的元素可以任意排列. (4)集合相等:构成两个集合的元素完全一样. 2.元素与集合的关系. (1)如果是集合的元素,就说属于,记作; (2)如果不是集合的元素,就说不属于,记作. 3.集合的表示方法. 用列举法表示集合时,不必考虑元素的顺序,只要元素相同,都是相等的集合. 用描述法表示集合时,需要把元素的属性表达清楚、全面,尽量用数学符号语言表达. 练习用区间表示集合时,需明确:单元素集合与不连续的数集是不能用区间表示的. 组织学生通过实例,加深对集合元素特征的理解. 教师举例或让学生自己举例,明确元素与集合的属于关系. 给出几个集合,看看可以用几种方法表示,学生思考、交流,得出结果. 加深对集合元素特征的理解. 会判断一个元素是不是集合中的元素. 熟练掌握集合的不同表示方法.
应用举例 例1 给出下列6个命题:①,②,③ ,④,⑤,⑥. 其中正确命题的个数为( ) A.4 B.3 C.2 D.1 练习:教材第8页练习A第1题. 例2 教材第7页例1. 例3 教材第8页例2. 练习:教材第9页练习A第3~5题. 教师操作课件,引导学生自己解决问题,让学生回答. 提示:先明确字母,,,表示的数集的意义,再判断所给的数与数集的关系是否正确. 学生分组练习,交流讨论,教师巡视,收集信息,及时评价. 学生自学例2、例3,教师引导、点拨学生对集合表示方法的选择. 学生练习,教师做好巡视指导. 锻炼学生的知识应用能力. 进一步加深对集合表示方法的学习,培养学生阅读自学的能力、抽象概括能力.
归纳小结 1.知识:(1)集合的含义、元素与集合的关系; (2)集合中元素的特性; (3)集合的表示方法:列举法、描述法; (4)区间及其表示. 2.方法:元素与集合的关系的判断方法;集合的表示方法;区间的表示方法. 学生相互交流收获与体会,并进行反思. 关注学生的自主体验,反思和发表本堂课的体验与收获.
布置作业 1.教材第9页练习B第1~4题. 2.教材第38~39页复习题A组第1,2题;B组第1题. 3.选做题:教材第40页C组第1题. 学生独立完成,教师批阅. 通过分层作业使学生巩固所学内容,并为有余力的学生提供进一步学习的机会.
板书设计
1.1.1 集合及其表示方法 一、问题 二、新课 1.集合与元素的概念 2.元素与集合的关系: 属于()和不属于() 3.集合中元素的特性: (1)确定性; (2)互异性; (3)无序性 4.常见数集的符号表示 5.集合的分类:有限集、无限集 6.集合的表示方法:列举法、描述法 7.区间及其表示 三、例题 例1 例2 例3 四、小结 1.知识 (1)集合的含义、元素与集合的关系 (2)集合中元素的特性 (3)集合的表示方法 (4)区间及其表示 2.方法
教学研讨
由于本节课是集合的起始课,所以在本案例中采用教师启发引导、学生探究学习的教学方法,结合生活中的一些实例,重视引导学生积极思考,使学生主动参与到教学中,并学会以下内容:
1.集合中元素的特性及应用,特别是互异性往往是检验参数是否符合题意的标准;
2.集合的表示方法,区分列举法与描述法的不同使用情境,对于有些集合会用另一种形式再表示;
3.区间是集合的另一种表达方法,比集合的应用更广泛,解题过程中,可以先写出集合,再转化为区间.
本案例以数学课程标准的要求为指导,体现了学生的主体地位.同时结合高考的要求适当拓展了教材,使学生的发散性思维得到拓展,最大限度地挖掘了学生的学习潜力,真正做到了对教材的“活学活用”.
教学环节 教学内容 师生互动 设计意图
问题引入 在初中代数不等式的解法一节中提到:一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称这个不等式的解集.不等式的解集的定义中涉及了“集合”,那么,集合的含义是什么呢?如何去表示一个集合呢? 教师提出问题,让学生回答,并对学生回答作出评价. 结合学生已有的知识经验,启发学生思考,激发学生的学习兴趣.
概念形成 1.阅读教材第3页“情境与问题”,思考需要分类的原因. 2.给出集合、元素的概念,思考:如何表示集合与元素? 在数学中,我们经常用“集合”来对所研究的对象进行分类.把一些能够确定的、不同的对象汇集在一起,就说由这些对象组成一个集合(有时简称为集),组成集合的每个对象都是这个集合的元素. 3.元素与集合的关系. 如果用表示高一(3)班全体学生组成的集合,用表示高一(3)班的一位同学,是高一(4)班的一位同学,那么,与集合分别有什么关系? 得出以下结论: 如果是集合的元素,就说属于集合,记作; 如果不是集合的元素,就说不属于集合,记作. 4.集合中元素的特点. 阅读教材第4页“尝试与发现”,回答问题. (1)你所在的班级中,身高不低于175cm的同学能组成一个集合吗? (2)你所在的班级中,高个子同学能组成一个集合吗?为什么? (3)不等式的所有解能组成一个集合吗? 5.空集. 不含任何元素的集合称为空集,记作. 6.几个常见的数集. 阅读教材第4~5页内容,认识常见数集的符号表示,回答“想一想”的问题. 常见数集的专用符号. :非负整数集(或自然数集)(全体非负整数的集合); 或:正整数集(非负整数集内排除0的集合); :整数集(全体整数的集合); :有理数集(全体有理数的集合); :实数集(全体实数的集合). 想一想: (1)无限循环小数可以表示成分数吗? (2)任何一个无限循环小数都是中的元素,这种说法正确吗? 7.集合的分类. 集合分类的标准是什么? 集合可以根据它含有的元素个数分为两类:含有有限个元素的集合称为有限集,含有无限个元素的集合称为无限集.空集可以看成包含0个元素的集合,所以空集是有限集. 8.集合的表示. 阅读教材中的相关内容,并思考、讨论下列问题: (1)要表示一个集合共有几种方式? (2)试比较自然语言、列举法和描述法在表示集合时,各自有什么特点?适用的对象分别是什么? (3)如何根据问题选择适当的集合表示方法? 9.区间. (1)一般区间的表示. 设,,且,规定如下: 定义名称符号数轴表示闭区间开区间半开半闭区间半开半闭区间
(2)特殊区间的表示. 定义符号
学生交流讨论. 教师操作课件,引导学生明确集合通常用英文大写字母,,,…表示,集合的元素通常用英文小写字母,,,…表示. 引导学生得出元素与集合的关系有两种:属于和不属于. 要求学生分组交流讨论,注意个别辅导,解答学生疑难.使学生明确集合元素的特性,即:确定性、互异性.只要构成两个集合的元素是一样的,我们就称这两个集合相等. 注意:集合中各元素没有先后顺序,即集合元素还具有无序性. 通过实例,理解空集的含义. 采取多种方式记忆数集的符号,引导学生规范使用符号. 通过实例,引导学生根据集合中元素的个数对集合进行分类. 要求学生掌握表示集合的两种方法:列举法和描述法,多举一些例子,多练习. 组织学生将一些数集表示为区间,进一步熟练掌握集合与区间的应用. 为理解集合的概念做铺垫,培养概括能力. 加深对集合概念的理解. 明确元素与集合之间的关系. 从形象到抽象,培养学生的数学抽象的核心素养. 理解空集的含义. 使学生经历数集的扩充过程,认识常用数集的符号. 体会有限集、无限集的概念. 使学生弄清楚集合表示方法的优缺点,体会它们存在的必要性和适用对象. 体会集合与区间的联系与区别.
概念深化 1.关于集合的元素的特征的理解. (1)确定性:设是一个给定的集合,是某一个具体对象,则或者是的元素,或者不是的元素,两种情况必有一种且只有一种成立. (2)互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素.相同的对象归入同一个集合时只能算作集合中的一个元素. (3)无序性:集合中的元素可以任意排列. (4)集合相等:构成两个集合的元素完全一样. 2.元素与集合的关系. (1)如果是集合的元素,就说属于,记作; (2)如果不是集合的元素,就说不属于,记作. 3.集合的表示方法. 用列举法表示集合时,不必考虑元素的顺序,只要元素相同,都是相等的集合. 用描述法表示集合时,需要把元素的属性表达清楚、全面,尽量用数学符号语言表达. 练习用区间表示集合时,需明确:单元素集合与不连续的数集是不能用区间表示的. 组织学生通过实例,加深对集合元素特征的理解. 教师举例或让学生自己举例,明确元素与集合的属于关系. 给出几个集合,看看可以用几种方法表示,学生思考、交流,得出结果. 加深对集合元素特征的理解. 会判断一个元素是不是集合中的元素. 熟练掌握集合的不同表示方法.
应用举例 例1 给出下列6个命题:①,②,③ ,④,⑤,⑥. 其中正确命题的个数为( ) A.4 B.3 C.2 D.1 练习:教材第8页练习A第1题. 例2 教材第7页例1. 例3 教材第8页例2. 练习:教材第9页练习A第3~5题. 教师操作课件,引导学生自己解决问题,让学生回答. 提示:先明确字母,,,表示的数集的意义,再判断所给的数与数集的关系是否正确. 学生分组练习,交流讨论,教师巡视,收集信息,及时评价. 学生自学例2、例3,教师引导、点拨学生对集合表示方法的选择. 学生练习,教师做好巡视指导. 锻炼学生的知识应用能力. 进一步加深对集合表示方法的学习,培养学生阅读自学的能力、抽象概括能力.
归纳小结 1.知识:(1)集合的含义、元素与集合的关系; (2)集合中元素的特性; (3)集合的表示方法:列举法、描述法; (4)区间及其表示. 2.方法:元素与集合的关系的判断方法;集合的表示方法;区间的表示方法. 学生相互交流收获与体会,并进行反思. 关注学生的自主体验,反思和发表本堂课的体验与收获.
布置作业 1.教材第9页练习B第1~4题. 2.教材第38~39页复习题A组第1,2题;B组第1题. 3.选做题:教材第40页C组第1题. 学生独立完成,教师批阅. 通过分层作业使学生巩固所学内容,并为有余力的学生提供进一步学习的机会.
板书设计
1.1.1 集合及其表示方法 一、问题 二、新课 1.集合与元素的概念 2.元素与集合的关系: 属于()和不属于() 3.集合中元素的特性: (1)确定性; (2)互异性; (3)无序性 4.常见数集的符号表示 5.集合的分类:有限集、无限集 6.集合的表示方法:列举法、描述法 7.区间及其表示 三、例题 例1 例2 例3 四、小结 1.知识 (1)集合的含义、元素与集合的关系 (2)集合中元素的特性 (3)集合的表示方法 (4)区间及其表示 2.方法
教学研讨
由于本节课是集合的起始课,所以在本案例中采用教师启发引导、学生探究学习的教学方法,结合生活中的一些实例,重视引导学生积极思考,使学生主动参与到教学中,并学会以下内容:
1.集合中元素的特性及应用,特别是互异性往往是检验参数是否符合题意的标准;
2.集合的表示方法,区分列举法与描述法的不同使用情境,对于有些集合会用另一种形式再表示;
3.区间是集合的另一种表达方法,比集合的应用更广泛,解题过程中,可以先写出集合,再转化为区间.
本案例以数学课程标准的要求为指导,体现了学生的主体地位.同时结合高考的要求适当拓展了教材,使学生的发散性思维得到拓展,最大限度地挖掘了学生的学习潜力,真正做到了对教材的“活学活用”.
