人教版七年级上册4.3.1 角 课件(共15张PPT)
文档属性
| 名称 | 人教版七年级上册4.3.1 角 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 409.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
第四章 几何图形初步
4.3.1 角
4.3 角
课时学习目标
1.理解角的两种描述方法,掌握角的表示方法.(重点)
2.认识直角、平角、周角。
4.会进行度、分、秒的简单换算.(难点)
思维激发
归纳:有公共端点的两条射线组成的图形叫做角
思考:什么是角呢?角是由什么组成的呢?
能从生活中举出角的例子吗?
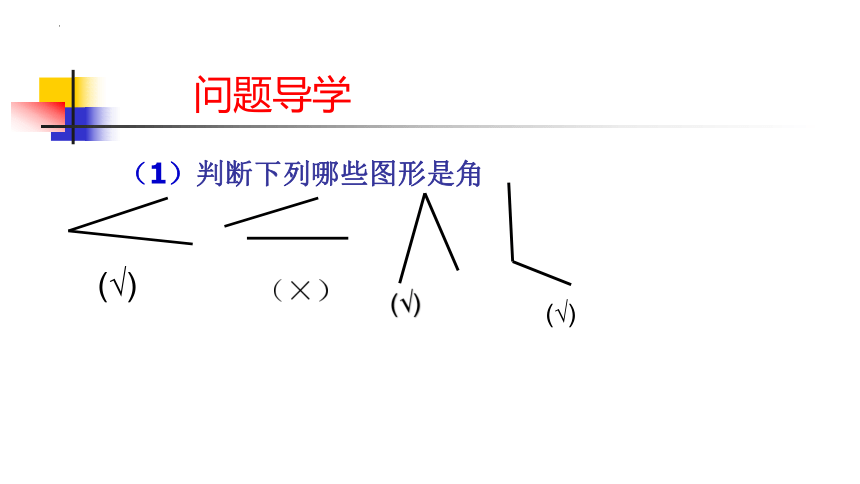
(1)判断下列哪些图形是角
问题导学
(√)
(×)
(√)
(√)
(1)下列说法正确的是( )
1.两条射线组成的图形叫做角.
2.角是一条线段绕着它的一个端点
旋转而成的图形.
3.有公共端点的两条线段组成的图形叫做角.
4.角是一条射线绕着他的端点旋转而成的图形.
问题导学
(2) 一周角等于_____° 1平角=______°
1°=______′ 1′=_____″
360
D
180
60
60
探析建构
观察下面实物,你发现这些实物给我们共同的形象是什么?
从你刚画的这些不同的图形中,能归纳出它们的共同特点吗?尝试去描述一下角是由什么组成的图形?
探析建构
有公共端点的两条射线组成的图形,叫做角
角是由两条具有公共端点的射线
组成的图形。
公共端点
顶点
射线
射线
边
边
公共端点
角的顶点
两条射线
角的边
始边
终边
O
A
B
O
A
顶点
(B)
射线OA绕点O旋转
当终止位置OB和起始位置OA成一条直线时,形成平角.
继续旋转,OB和OA重合时,形成周角.
在不做特别说明的情况下,我们说的角都指不大于平角的角
O
B
A
O
B
探析建构
A
B
A
C
角的表示方法
记作:∠BAC 或∠CAB
O
α
记作∠α
记作∠1
O
A
B
记作:∠O
1
如图,以O为顶点的角有几个,请分别把他们
读出来。
O
A
B
C
D
E
解:共有10个角,
分别是:
∠AOB,∠AOC,
∠AOD,∠AOE,
∠BOC,∠BOD,
∠BOE,∠COD,
∠COE,∠DOE。
训练迁移
角的度量
度,分,秒
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″
角的度量工具:
量角器
角的度量单位:
360
180
1周角= °;
1平角= °.
怎么知道这个角的大小?
度分秒的互化
⑴ 57.32 = ′ ″ ;
⑵ 17°6′36″= ° ;
解析:57.32 =57 +0.32×60′
=57 +19.2′
=57 19′+0.2×60″
=57 19′12″
解析:17°6′36″=17°+6′+(36/60)′
=17°+6.6′
=17 +(6.6/60)°
=17.11
按1°=60′,1′=60″先把度化成分,再把分化成秒
(小数化整数)
按1″=(1/60)′,1′=(1/60)°先把秒化成分,再把分化成度(整数化小数)
训练迁移
38.15°= ° ′;
小结
1.角的定义一:
有公共端点的两条射线组成的图形
叫做角,这个公共端点叫做角的顶点,这
两条射线叫做角的边。
2.角的定义二:
角可以看成是一条射线绕着它的
端点从一个位置旋转到另一个位置所形成
的图形。射线旋转时经过的平面部分叫角
的内部。
1、如图,棱锥表面上有几个角,请把它们表示出来?
A
B
C
D
扩展提升
∠ BAC ∠CAD ∠BAD
∠ABC ∠ABD ∠CBD
∠ACB ∠ACD ∠BCD
∠ ADB ∠ADC ∠BDC
第四章 几何图形初步
4.3.1 角
4.3 角
课时学习目标
1.理解角的两种描述方法,掌握角的表示方法.(重点)
2.认识直角、平角、周角。
4.会进行度、分、秒的简单换算.(难点)
思维激发
归纳:有公共端点的两条射线组成的图形叫做角
思考:什么是角呢?角是由什么组成的呢?
能从生活中举出角的例子吗?
(1)判断下列哪些图形是角
问题导学
(√)
(×)
(√)
(√)
(1)下列说法正确的是( )
1.两条射线组成的图形叫做角.
2.角是一条线段绕着它的一个端点
旋转而成的图形.
3.有公共端点的两条线段组成的图形叫做角.
4.角是一条射线绕着他的端点旋转而成的图形.
问题导学
(2) 一周角等于_____° 1平角=______°
1°=______′ 1′=_____″
360
D
180
60
60
探析建构
观察下面实物,你发现这些实物给我们共同的形象是什么?
从你刚画的这些不同的图形中,能归纳出它们的共同特点吗?尝试去描述一下角是由什么组成的图形?
探析建构
有公共端点的两条射线组成的图形,叫做角
角是由两条具有公共端点的射线
组成的图形。
公共端点
顶点
射线
射线
边
边
公共端点
角的顶点
两条射线
角的边
始边
终边
O
A
B
O
A
顶点
(B)
射线OA绕点O旋转
当终止位置OB和起始位置OA成一条直线时,形成平角.
继续旋转,OB和OA重合时,形成周角.
在不做特别说明的情况下,我们说的角都指不大于平角的角
O
B
A
O
B
探析建构
A
B
A
C
角的表示方法
记作:∠BAC 或∠CAB
O
α
记作∠α
记作∠1
O
A
B
记作:∠O
1
如图,以O为顶点的角有几个,请分别把他们
读出来。
O
A
B
C
D
E
解:共有10个角,
分别是:
∠AOB,∠AOC,
∠AOD,∠AOE,
∠BOC,∠BOD,
∠BOE,∠COD,
∠COE,∠DOE。
训练迁移
角的度量
度,分,秒
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″
角的度量工具:
量角器
角的度量单位:
360
180
1周角= °;
1平角= °.
怎么知道这个角的大小?
度分秒的互化
⑴ 57.32 = ′ ″ ;
⑵ 17°6′36″= ° ;
解析:57.32 =57 +0.32×60′
=57 +19.2′
=57 19′+0.2×60″
=57 19′12″
解析:17°6′36″=17°+6′+(36/60)′
=17°+6.6′
=17 +(6.6/60)°
=17.11
按1°=60′,1′=60″先把度化成分,再把分化成秒
(小数化整数)
按1″=(1/60)′,1′=(1/60)°先把秒化成分,再把分化成度(整数化小数)
训练迁移
38.15°= ° ′;
小结
1.角的定义一:
有公共端点的两条射线组成的图形
叫做角,这个公共端点叫做角的顶点,这
两条射线叫做角的边。
2.角的定义二:
角可以看成是一条射线绕着它的
端点从一个位置旋转到另一个位置所形成
的图形。射线旋转时经过的平面部分叫角
的内部。
1、如图,棱锥表面上有几个角,请把它们表示出来?
A
B
C
D
扩展提升
∠ BAC ∠CAD ∠BAD
∠ABC ∠ABD ∠CBD
∠ACB ∠ACD ∠BCD
∠ ADB ∠ADC ∠BDC
