4.1.1 第2课时 从不同的方向看立体图形和立体图形的展开图 课件(共53张PPT)
文档属性
| 名称 | 4.1.1 第2课时 从不同的方向看立体图形和立体图形的展开图 课件(共53张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 10:42:04 | ||
图片预览




文档简介
(共53张PPT)
4.1.1 立体图形与平面图形
第2课时 从不同的方向看立体图形和立体图形的展开图
第四章 几何图形初步
1. 了解立体图形与平面图形之间的联系.
2. 能画出简单立体图形从不同方向看得到的平面图形.
3. 了解研究立体图形的方法,体会一个立体图形按照不同方式展开可得到不同的平面展开图.
4. 通过展开与折叠,了解棱柱、棱锥、圆柱、圆锥、长方体、正方体的表面展开图或根据展开图判断立体图形.
引入新课
合作探究
典例分析
针对训练
针对训练
合作探究
布置作业
感受中考
课堂小结
当堂巩固
能力提升
引入新课
题西林壁 ---苏轼
横看成岭侧成峰,远近高低各不同.
不识庐山真面目,只缘身在此山中.
“横看成岭侧成峰”一句中,蕴含了怎样的数学道理?
引入新课
漫画“6”与“9”
思考:他们为什么会出现争执?
引入新课
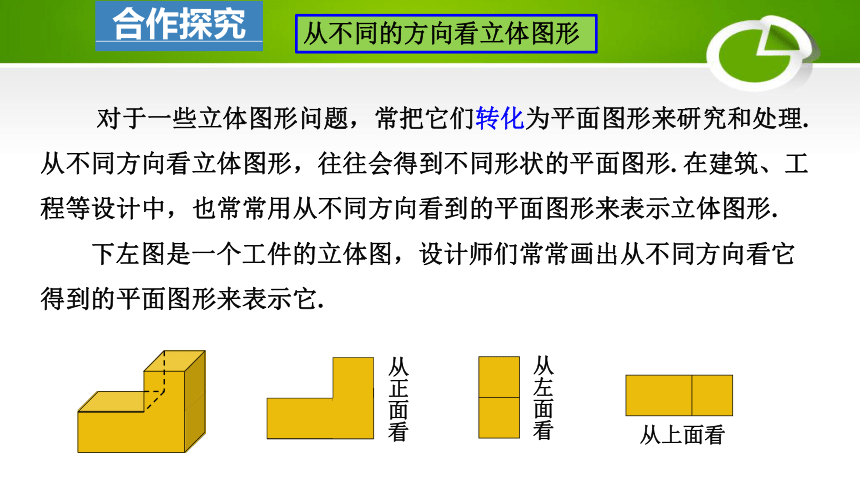
对于一些立体图形问题,常把它们转化为平面图形来研究和处理.从不同方向看立体图形,往往会得到不同形状的平面图形. 在建筑、工程等设计中,也常常用从不同方向看到的平面图形来表示立体图形.
下左图是一个工件的立体图,设计师们常常画出从不同方向看它得到的平面图形来表示它.
从正面看
从左面看
从上面看
从不同的方向看立体图形
合作探究
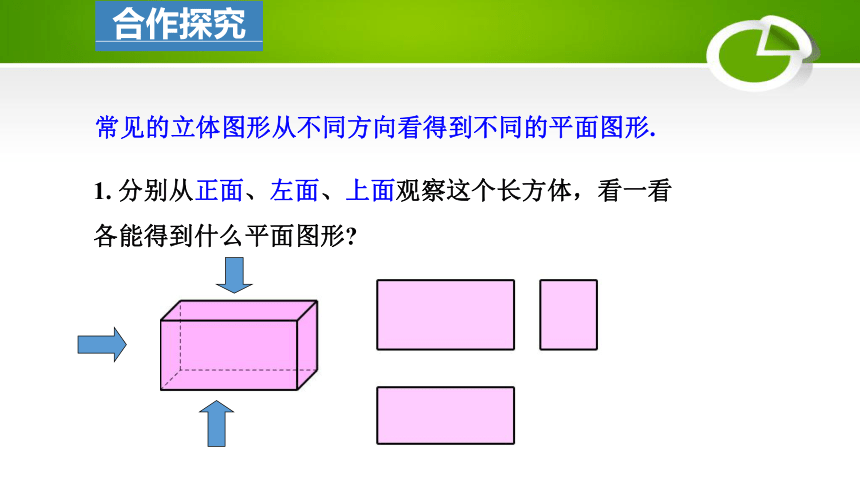
1. 分别从正面、左面、上面观察这个长方体,看一看各能得到什么平面图形
常见的立体图形从不同方向看得到不同的平面图形.
合作探究
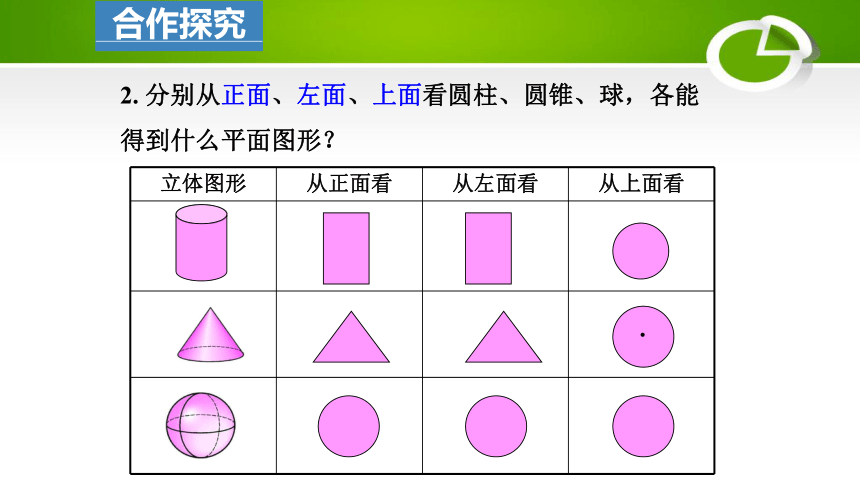
立体图形 从正面看 从左面看 从上面看
2. 分别从正面、左面、上面看圆柱、圆锥、球,各能得到什么平面图形?
.
合作探究
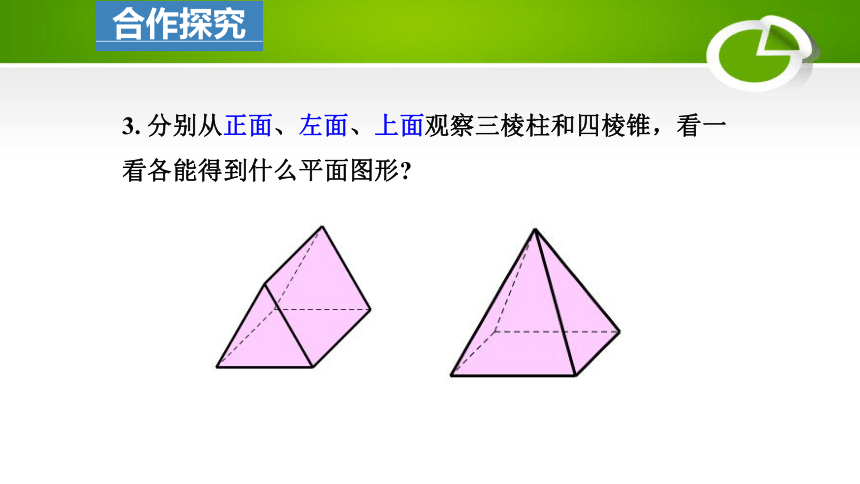
3. 分别从正面、左面、上面观察三棱柱和四棱锥,看一看各能得到什么平面图形
合作探究
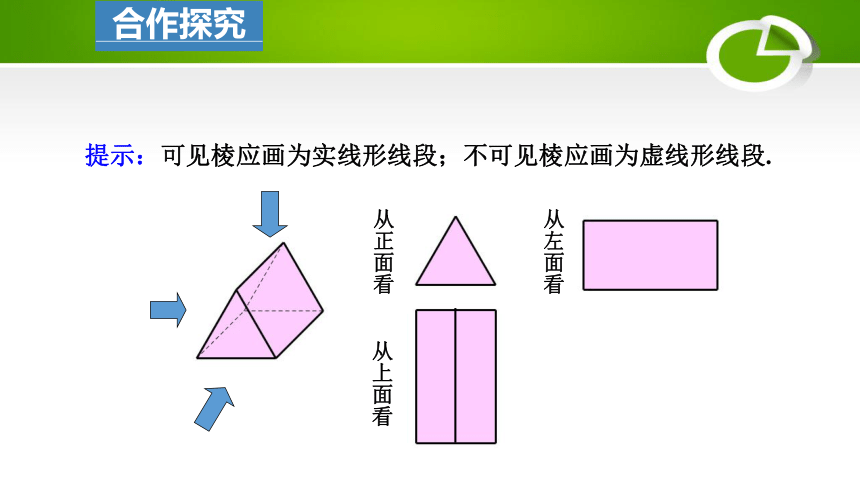
从正面看
从左面看
从上面看
提示:可见棱应画为实线形线段;不可见棱应画为虚线形线段.
合作探究
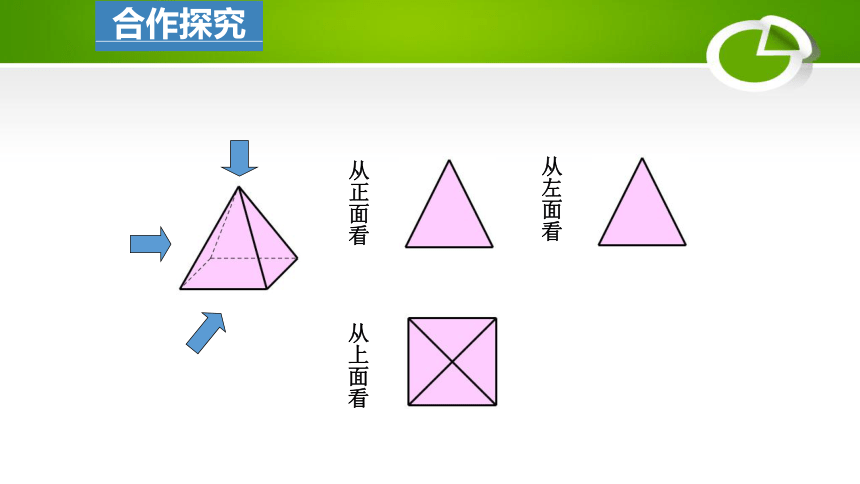
从正面看
从左面看
从上面看
合作探究
如图,右面三幅图分别是从哪个方向看这个棱柱得到的?
上面 正面 左面
合作探究
正面
左面
上面
右图是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个图形,各能得到什么平面图形?
组合体从不同方向看得到不同的平面图形
合作探究
例:如图是由若干小正方体搭成的几何体,我们分别从正面看、从左面看和从上面看得到的平面图形分别是怎样的呢?请同学们尝试画一画.
典例分析
从上面看
从左面看
从正面看
从正面看
从左面看
从上面看
典例分析
1. 从正面、左面、上面看这个由正方体组合成的立体图形各能得到什么平面图形?
从正面看 从左面看 从上面看
针对训练
2. 分别从正面、左面、上面观察下面的立体图形,各能得到什么平面图形?
立体图形 正面 左面 上面
针对训练
3. 分别画出从正面、上面和左面观察如图所示的立体图形后所得到的平面图形.
针对训练
4. 如图①,讲台上放着一本数学书,书上面放着一个粉笔盒,若这个组合图形从上面看到的图形如图②,则这个组合图形从左面看到的图形是( ).
A
针对训练
5. 如图,分别从正面、左面、上面观察这个立体图形,请画出你看到的平面图形.
针对训练
6. 说出下面三个平面图形分别是物体从哪里看到的?
从正面看
从上面看
从左面看
针对训练
7. 分别从正面、左面、上面看一个由若干个正方体组成的立体图形,得到的平面图形如下图所示,你能搭出这个立体图形吗?动手试试看!
正面
左面
上面
针对训练
如下图,要设计、制作一个长方体形状的墨水瓶包装盒,除了美术设计以外,还要了解它展开后的形状,即要根据它的平面展开图来裁剪纸张,这就需要我们了解一些简单立体图形的展开图.
许多立体图形是由一些平面图形围成的,将它们适当地剪开,就可以展开成平面图形.
立体图形的展开图
合作探究
将一个正方体的表面沿某些棱剪开,能展成哪些平面图形?
友情提示:
沿着棱剪
展开后是一
个平面图形
把一个包装盒剪开铺平,看看它的展开图由哪些平面图形组成?再把展开的纸板复原为包装盒,体会立体图形与平面图形的关系.
合作探究
思考:1. 这些正方体展开图可以分为几种?
2. 观察上面的11种正方体的展开图有没有什么规律?
哪几号展开图可以分为一类,为什么?
1
2
3
4
5
6
7
8
9
10
11
正方体的展开图
合作探究
合作探究
合作探究
合作探究
相
对
两
面
不
相
连
蓝
黄
左右隔一列
上下隔一行
正方体相对两个面在其
展开图中的位置有什么特点
合作探究
蓝
黄
红
巧记正方体的展开图口诀:
正方体盒巧展开,
六个面儿七刀裁,
十一类图记分明;
一四一呈6种,
二三一有3种,
二二二与三三各1种;
对面相隔不相连,
识图巧排“凹”和“田”.
总结归纳
A B C D
C
1. 下列图形中,不是正方体表面展开图的是 ( )
针对训练
2. 如图,这些图形都是正方体的平面展开图吗?如果不能确定,折一折,试一试,你还能再画出一些正方体的平面展开图吗?
√
×
√
√
√
√
针对训练
利
胜
持
是
就
坚
3.“坚”在下,“就”在后,“胜”和“利”在哪里?
一个多面体的展开图中,在同一直线上的相邻的三个线框中,首尾两个线框是立体图形中相对的两个面.
“胜”在上,“利”在前.
针对训练
你还记得长方体和圆柱的侧面展开图吗?下图是一些立体图形的展开图,用它们能围成什么样的立体图形?把它们画在一张硬纸片上,剪下来,折叠、粘贴,看看得到的图形和你想象的是否相同.
合作探究
1. 下面图形是一些多面体的表面展开图,你能说出这些多面体的名字吗?
当堂巩固
2. 下列立体图形的平面展开图是什么
当堂巩固
展开
当堂巩固
展开
当堂巩固
1. 下图所示的从正面、上面看到的图形对应的是 ( )
B
A B C D
能力提升
2. 下图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是 ( )
B
能力提升
3. 下图是由一些相同的小正方体构成的几何体的从正面、左面、上面看得到的三个平面图形,这些相同的小正方体的个数是 ( )
A.4个
B.5个
C.6个
D.7个
B
能力提升
4. 下列的三幅平面图是三棱柱的表面展开图的有(多选) ( )
A、C
A B C
能力提升
5. 如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:a= ;b= ;c= .
-2
-7
1
c
7
-1
b
a
2
能力提升
1.(2022 河北)①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
【解答】解:由题意知,组合后的几何体是长方体且由6个小正方体构成,
所以①④符合要求,
故选:D.
感受中考
2.(2022 自贡)如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
【解答】解:根据“点动成线,线动成面,面动成体”,
将矩形纸片ABCD绕边CD所在直线旋转一周,所得到的立体图形是圆柱.
故选:A.
A. B. C. D.
感受中考
3.(2分)(2021 北京1/28)如图是某几何体的展开图,该几何体是( )
A.长方体 B.圆柱 C.圆锥 D.三棱柱
【解答】解:∵圆柱的展开图为两个圆和一个长方形,
∴展开图可得此几何体为圆柱.
故选:B.
【点评】此题主要考查了由展开图得几何体,关键是考查空间想象能力.
感受中考
4.(3分)(2021 广东6/25)下列图形是正方体展开图的个数为( )
A.1个 B.2个 C.3个 D.4个
感受中考
【分析】由平面图形的折叠及正方体的展开图的特征解答即可.
【解答】解:由正方体的四个侧面和底面的特征可知,可以拼成正方体是下列三个图形:
故这些图形是正方体展开图的个数为3个.
故选:C.
【点评】本题考查了几何体的展开图.解题时勿忘记四棱柱的特征及正方体展开图的各种情形.
感受中考
5.(3分)(2021 河北6/26)一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )
A.A代 B.B代 C.C代 D.B代
感受中考
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点对各选项分析判断后利用排除法求解.
【解答】解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
A与点数是1的对面,B与点数是2的对面,C与点数是4的对面,
∵骰子相对两面的点数之和为7,
∴A代表的点数是6,B代表的点数是5,C代表的点数是4.
故选:A.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体是空间图形,从相对面入手,分析及解答问题.
感受中考
课堂小结
常见几何体的展开图:
圆锥 四棱锥 长方体 三棱柱
三棱锥 三棱柱 正方体 圆柱
这节课我们主要学习了从不同方向看立体图形得到平面图形及常见几何体的展开图,谈一谈自己有哪些学习成果.
布置作业
P121:习题4.1:第4题.
P122:习题4.1:第5、6、7题.
P123:习题4.1:第12、13题.
4.1.1 立体图形与平面图形
第2课时 从不同的方向看立体图形和立体图形的展开图
第四章 几何图形初步
1. 了解立体图形与平面图形之间的联系.
2. 能画出简单立体图形从不同方向看得到的平面图形.
3. 了解研究立体图形的方法,体会一个立体图形按照不同方式展开可得到不同的平面展开图.
4. 通过展开与折叠,了解棱柱、棱锥、圆柱、圆锥、长方体、正方体的表面展开图或根据展开图判断立体图形.
引入新课
合作探究
典例分析
针对训练
针对训练
合作探究
布置作业
感受中考
课堂小结
当堂巩固
能力提升
引入新课
题西林壁 ---苏轼
横看成岭侧成峰,远近高低各不同.
不识庐山真面目,只缘身在此山中.
“横看成岭侧成峰”一句中,蕴含了怎样的数学道理?
引入新课
漫画“6”与“9”
思考:他们为什么会出现争执?
引入新课
对于一些立体图形问题,常把它们转化为平面图形来研究和处理.从不同方向看立体图形,往往会得到不同形状的平面图形. 在建筑、工程等设计中,也常常用从不同方向看到的平面图形来表示立体图形.
下左图是一个工件的立体图,设计师们常常画出从不同方向看它得到的平面图形来表示它.
从正面看
从左面看
从上面看
从不同的方向看立体图形
合作探究
1. 分别从正面、左面、上面观察这个长方体,看一看各能得到什么平面图形
常见的立体图形从不同方向看得到不同的平面图形.
合作探究
立体图形 从正面看 从左面看 从上面看
2. 分别从正面、左面、上面看圆柱、圆锥、球,各能得到什么平面图形?
.
合作探究
3. 分别从正面、左面、上面观察三棱柱和四棱锥,看一看各能得到什么平面图形
合作探究
从正面看
从左面看
从上面看
提示:可见棱应画为实线形线段;不可见棱应画为虚线形线段.
合作探究
从正面看
从左面看
从上面看
合作探究
如图,右面三幅图分别是从哪个方向看这个棱柱得到的?
上面 正面 左面
合作探究
正面
左面
上面
右图是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个图形,各能得到什么平面图形?
组合体从不同方向看得到不同的平面图形
合作探究
例:如图是由若干小正方体搭成的几何体,我们分别从正面看、从左面看和从上面看得到的平面图形分别是怎样的呢?请同学们尝试画一画.
典例分析
从上面看
从左面看
从正面看
从正面看
从左面看
从上面看
典例分析
1. 从正面、左面、上面看这个由正方体组合成的立体图形各能得到什么平面图形?
从正面看 从左面看 从上面看
针对训练
2. 分别从正面、左面、上面观察下面的立体图形,各能得到什么平面图形?
立体图形 正面 左面 上面
针对训练
3. 分别画出从正面、上面和左面观察如图所示的立体图形后所得到的平面图形.
针对训练
4. 如图①,讲台上放着一本数学书,书上面放着一个粉笔盒,若这个组合图形从上面看到的图形如图②,则这个组合图形从左面看到的图形是( ).
A
针对训练
5. 如图,分别从正面、左面、上面观察这个立体图形,请画出你看到的平面图形.
针对训练
6. 说出下面三个平面图形分别是物体从哪里看到的?
从正面看
从上面看
从左面看
针对训练
7. 分别从正面、左面、上面看一个由若干个正方体组成的立体图形,得到的平面图形如下图所示,你能搭出这个立体图形吗?动手试试看!
正面
左面
上面
针对训练
如下图,要设计、制作一个长方体形状的墨水瓶包装盒,除了美术设计以外,还要了解它展开后的形状,即要根据它的平面展开图来裁剪纸张,这就需要我们了解一些简单立体图形的展开图.
许多立体图形是由一些平面图形围成的,将它们适当地剪开,就可以展开成平面图形.
立体图形的展开图
合作探究
将一个正方体的表面沿某些棱剪开,能展成哪些平面图形?
友情提示:
沿着棱剪
展开后是一
个平面图形
把一个包装盒剪开铺平,看看它的展开图由哪些平面图形组成?再把展开的纸板复原为包装盒,体会立体图形与平面图形的关系.
合作探究
思考:1. 这些正方体展开图可以分为几种?
2. 观察上面的11种正方体的展开图有没有什么规律?
哪几号展开图可以分为一类,为什么?
1
2
3
4
5
6
7
8
9
10
11
正方体的展开图
合作探究
合作探究
合作探究
合作探究
相
对
两
面
不
相
连
蓝
黄
左右隔一列
上下隔一行
正方体相对两个面在其
展开图中的位置有什么特点
合作探究
蓝
黄
红
巧记正方体的展开图口诀:
正方体盒巧展开,
六个面儿七刀裁,
十一类图记分明;
一四一呈6种,
二三一有3种,
二二二与三三各1种;
对面相隔不相连,
识图巧排“凹”和“田”.
总结归纳
A B C D
C
1. 下列图形中,不是正方体表面展开图的是 ( )
针对训练
2. 如图,这些图形都是正方体的平面展开图吗?如果不能确定,折一折,试一试,你还能再画出一些正方体的平面展开图吗?
√
×
√
√
√
√
针对训练
利
胜
持
是
就
坚
3.“坚”在下,“就”在后,“胜”和“利”在哪里?
一个多面体的展开图中,在同一直线上的相邻的三个线框中,首尾两个线框是立体图形中相对的两个面.
“胜”在上,“利”在前.
针对训练
你还记得长方体和圆柱的侧面展开图吗?下图是一些立体图形的展开图,用它们能围成什么样的立体图形?把它们画在一张硬纸片上,剪下来,折叠、粘贴,看看得到的图形和你想象的是否相同.
合作探究
1. 下面图形是一些多面体的表面展开图,你能说出这些多面体的名字吗?
当堂巩固
2. 下列立体图形的平面展开图是什么
当堂巩固
展开
当堂巩固
展开
当堂巩固
1. 下图所示的从正面、上面看到的图形对应的是 ( )
B
A B C D
能力提升
2. 下图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是 ( )
B
能力提升
3. 下图是由一些相同的小正方体构成的几何体的从正面、左面、上面看得到的三个平面图形,这些相同的小正方体的个数是 ( )
A.4个
B.5个
C.6个
D.7个
B
能力提升
4. 下列的三幅平面图是三棱柱的表面展开图的有(多选) ( )
A、C
A B C
能力提升
5. 如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:a= ;b= ;c= .
-2
-7
1
c
7
-1
b
a
2
能力提升
1.(2022 河北)①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
【解答】解:由题意知,组合后的几何体是长方体且由6个小正方体构成,
所以①④符合要求,
故选:D.
感受中考
2.(2022 自贡)如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
【解答】解:根据“点动成线,线动成面,面动成体”,
将矩形纸片ABCD绕边CD所在直线旋转一周,所得到的立体图形是圆柱.
故选:A.
A. B. C. D.
感受中考
3.(2分)(2021 北京1/28)如图是某几何体的展开图,该几何体是( )
A.长方体 B.圆柱 C.圆锥 D.三棱柱
【解答】解:∵圆柱的展开图为两个圆和一个长方形,
∴展开图可得此几何体为圆柱.
故选:B.
【点评】此题主要考查了由展开图得几何体,关键是考查空间想象能力.
感受中考
4.(3分)(2021 广东6/25)下列图形是正方体展开图的个数为( )
A.1个 B.2个 C.3个 D.4个
感受中考
【分析】由平面图形的折叠及正方体的展开图的特征解答即可.
【解答】解:由正方体的四个侧面和底面的特征可知,可以拼成正方体是下列三个图形:
故这些图形是正方体展开图的个数为3个.
故选:C.
【点评】本题考查了几何体的展开图.解题时勿忘记四棱柱的特征及正方体展开图的各种情形.
感受中考
5.(3分)(2021 河北6/26)一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )
A.A代 B.B代 C.C代 D.B代
感受中考
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点对各选项分析判断后利用排除法求解.
【解答】解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
A与点数是1的对面,B与点数是2的对面,C与点数是4的对面,
∵骰子相对两面的点数之和为7,
∴A代表的点数是6,B代表的点数是5,C代表的点数是4.
故选:A.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体是空间图形,从相对面入手,分析及解答问题.
感受中考
课堂小结
常见几何体的展开图:
圆锥 四棱锥 长方体 三棱柱
三棱锥 三棱柱 正方体 圆柱
这节课我们主要学习了从不同方向看立体图形得到平面图形及常见几何体的展开图,谈一谈自己有哪些学习成果.
布置作业
P121:习题4.1:第4题.
P122:习题4.1:第5、6、7题.
P123:习题4.1:第12、13题.
