6.1 图上距离与实际距离(课件)(共39张PPT)
文档属性
| 名称 | 6.1 图上距离与实际距离(课件)(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 11:47:58 | ||
图片预览











文档简介
(共39张PPT)
图上距离与实际距离
The distance on the graph and the actual distance
苏科版九年级下册第6章图形的相似
教学目标
01
了解线段的比
02
理解比例尺、成比例线段、比例、比例中项等概念
03
掌握比例的基本性质以及比例的其他性质
两条线段的比
知识精讲
情境引入
01
Q1:两组图中A、B之间有何关系?
A B
A B
【分析】形状相同、大小相等——全等
知识精讲
情境引入
01
Q2:两组图中A、B之间有何关系?
A B
A B
【分析】形状相同、但是大小不等
知识精讲
情境引入
01
Q3:怎样通过具体数值描述出它们的大小关系呢?(以冰墩墩为例)
A B
A B
在冰墩墩A上取两点C、D,连接CD,测量其长度,记为a
在冰墩墩B上取相应的两点C1、D1,连接C1D1,测量其长度,记为b
C
D
C1
D1
两个冰墩墩图形大小的比,即CD:C1D1,即a:b,
因此,要研究形状相同、大小不同的图形,要先研究对应线段(长度)的比
02
知识精讲
两条线段的比
两条线段长度的比,叫做两条线段的比
两条线段的比a:b中,a叫做比的前项,b叫做比的后项
【两条线段的比具有顺序性,要明确前项与后项】
知识精讲
例1、已知AB长为1dm,CD长为2cm,则AB:CD=________.
【分析】
∵AB=1dm=10cm
∴AB:CD=10:2=5:1
【总结】
(1)计算线段的比,即计算线段长度的比
(2)需保证长度的单位统一
【两条线段的比】
知识精讲
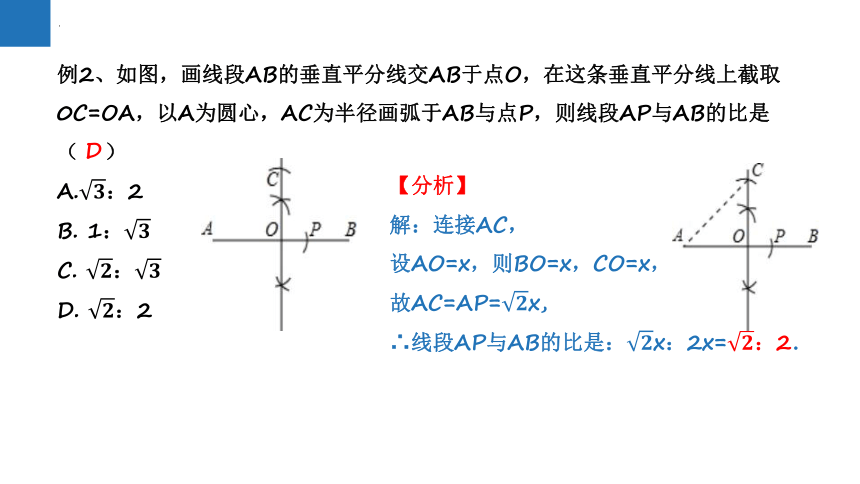
例2、如图,画线段AB的垂直平分线交AB于点O,在这条垂直平分线上截取0C=OA,以A为圆心,AC为半径画弧于AB与点P,则线段AP与AB的比是( )
A.:2
B. 1:
C. :
D. :2
【分析】
解:连接AC,
设AO=x,则BO=x,CO=x,
故AC=AP=x,
∴线段AP与AB的比是:x:2x=:2.
D
成比例线段/比例
知识精讲
情境引入
01
在上面两幅比例尺不同的江苏省地图中,设连接南京与徐州的线段长分别为a、b,连接南京与连云港的线段长分别为c、d,问:
(1)比例尺1:8000000与比例尺1:16000000的含义是什么?
(2)a:b与c:d的比值是否相等?
知识精讲
情境引入
01
【分析】(1)∵比例尺=,∴图1:=,图2:=
(1)比例尺1:8000000与比例尺1:16000000的含义是什么?
知识精讲
情境引入
01
(2)a:b与c:d的比值是否相等?
根据比例尺可得:=2=
先度量出a、b、c、d的大小,再分别计算和的值,
可得:=
【分析】(2)
两种方法都可以哦~
02
知识精讲
成比例线段
1、在四条线段中,如果两条线段的比等于另两条线段的比,
那么这四条线段叫做成比例线段,简称比例线段
注意:四条线段成比例时,要把这四条线段按顺序排列,不能随意颠倒
2、比例:两个比相等的式子叫做比例,如 a:b=c:d
(1)比例的四个项a、b、c、d分别叫做第一、二、三、四比例项
(2)其中a和d又叫做比例外项,b和c叫做比例内项
(3)在比例式a:b=b:c中,b叫做a和c的比例中项
02
知识精讲
Q1:下图中,哪两个矩形的长和宽是成比例线段?
9
6
8
4
6
4
(1) (2) (3)
【分析】
∵(1)长:宽=9:6=3:2;(2)长:宽=8:4=2:1;
(3)长:宽=6:4=3:2
∴第1个矩形和第3个矩形的长和宽是成比例线段
02
知识精讲
Q2:如下图,线段A1B1、B1C1、A2B2、B2C2的端点都在边长为1的小正方形的顶点上,问:这四条线段是成比例线段吗?
【分析】
根据题意:
A1B1=2,B1C1=2;A2B2=,B2C2=
将线段按照从小到大的顺序排列:
即A2B2、A1B1、B2C2、B1C1
∵A2B2:A1B1=:2=1:2 ;
B2C2:B1C1=:2=1:2
∴A2B2:A1B1=B2C2:B1C1
∴这四条线段是成比例线段
C2
C1
B1
B2
A1
A2
02
知识精讲
3、判断四条线段是否是成比例线段的方法:
(1)单位统一——确保四条线段的单位统一
(2)排序——将线段按照从小到大的顺序排列
(3)计算——分别计算排序后的前两条线段的比、后两条线段的比
(4)看——看比是否相等
例3-1、在比例尺是1∶10000的地图上,图距25mm,则实距是________m;如果实距为500m,其图距为________cm.
【比例尺问题】
【分析】
∵比例尺=,
∴=,=
∴实际距离=250000mm=250m,图上距离=0.05m=5cm
【注意】切换单位
250
5
例3-2、在比例尺为1∶10000的地图上,一块面积为2cm 的区域表示的实际面积是___________m .
【分析】
∵比例尺==1∶10000,
∴==,
∴实际面积=200000000cm2=20000m2
【注意】
(1)面积比要平方
(2)切换单位again
20000
例4、下列各组中的四条线段成比例的是( )
A.1cm,2cm,3cm,4cm B.1cm,2cm,20cm,40cm
C.4cm,2cm,5cm,3cm D.5cm,10cm,15cm,20cm
【分析】
A.1×4≠2×3,∴四条线段不成比例;
B.1×40=2×20,∴四条线段成比例;
C.排序:2cm,3cm,4cm,5cm,2×5≠3×4,∴四条线段不成比例;
D.5×20≠10×15,∴四条线段不成比例.
【成比例线段的判断】
B
例5-1、线段a=2cm,b=3cm,c=lcm,那么a、b、c的第四比例项d=________.
例5-2、线段a=6cm,b=2cm,则a、b、a+b的第四比例项是________cm.
【比例的有关概念】
【分析5-1】
∵=,
∴=,
∴d=1.5cm
【分析5-2】
设第四比例项为d
∵=,
∴=,
∴d=cm
【注意】单位不能漏
1.5cm
比例的性质
02
知识精讲
1、比例的基本性质(小学已学):
(1)如果a:b=c:d,那么ad=bc
(2)反过来,如果ad=bc(b≠0,d≠0),那么a:b=c:d
2、推广:
(1)特别地,如果a:b=b:c,那么ac=b2,即比例外项的积=比例中项的平方
(2)如果ad=bc(a、b、c、d均不为0),那么=,=,=,=
比例的基本性质
02
知识精讲
Q1:已知=,判断与是否相等
【分析】
∵=,
∴±1=±1,
∴=
合比定理与分比定理
02
知识精讲
Q2:已知=,判断与是否相等
【分析】
设==k(k≠1),则a=kb,c=kd
∴==,==
∴=
合分比定理
【总结】
本问方法为:设“k”法
02
知识精讲
Q3:已知=,判断与是否相等
【分析】
设==k,则a=kb,c=kd
∴==k==
等比定理
【总结】
本问方法也为:设“k”法
02
知识精讲
3、比例的其他性质
(1)合比定理:如果=,那么=
分比定理:如果=,那么=
(2)合分比定理:如果=(a-b≠0,c-d≠0),那么=
比例的其他性质
02
知识精讲
(3)等比定理:如果=(b±d≠0),那么==
进一步推广:
如果===(分母和≠0),那么==
比例的其他性质
例6-1、若a=4cm,b=9cm,则线段a,b的比例中项是________cm.
【比例的基本性质——求比例中项】
【分析】
设比例中项为m
∵ab=m2,
∴(4cm)×(9cm)=m2,
∵m>0
∴m=6cm
6
例6-2、已知三个数3、6、x,要使其中一个数是其他两数的比例中项,则x的取值是____________________________.
【分析】比例中项指代不明,需分类讨论
①设3为比例中项,则6x=32,解得:x=;
②设6为比例中项,则3x=62,解得:x=12;
③设x为比例中项,则3×6=x2,解得:x=;
综上,x=或x=12或x=
x=或x=12或x=
例7、若a:b=3:4,b:c=1:2,则a:c=________.
【分析】
∵a:b=3:4,b:c=1:2=4:8,
∴a:b:c=3:4:8,
∴a:c=3:8
【比例的其他性质】
3:8
【总结】
本题方法:把b转化成同一个数,进行连比
例8、已知=,那么=________.
【分析】
∵=,
∴-1=-1,即=-,
∴=
例9、已知=,那么=________.
【分析】法一:
∵=,
∴a=b,
∴===4
4
法二:
∵=,
∴设a=3k,b=5k,
∴===4
【对比总结】
设“k”法更简单明了
例10、已知a:b:c=9:11:14,且a+b+c=68,则3a-2b+c=________.
【分析】
∵a:b:c=9:11:14,且a+b+c=68,
∴设a=9k,b=11k,c=14k,
∴9k+11k+14k=68,解得:k=2,
∴a=18,b=22,c=28,
∴3a-2b+c=38
38
例11、已知===,且b+d+f≠0,则=________.
【分析】
∵===,且b+d+f≠0,
∴根据等比定理:=
【总结】
直接用设“k”法推导出的等比定理
课后总结1
两条线段长度的比,叫做两条线段的比
两条线段的比a:b中,a叫做比的前项,b叫做比的后项
【两条线段的比具有顺序性,要明确前项与后项】
课后总结2
3、判断四条线段是否是成比例线段的方法:
(1)单位统一——确保四条线段的单位统一
(2)排序——将线段按照从小到大的顺序排列
(3)计算——分别计算排序后的前两条线段的比、后两条线段的比
(4)看——看比是否相等
1、在四条线段中,如果两条线段的比等于另两条线段的比,
那么这四条线段叫做成比例线段,简称比例线段
注意:四条线段成比例时,要把这四条线段按顺序排列,不能随意颠倒
2、比例:两个比相等的式子叫做比例,如 a:b=c:d
(1)比例的四个项a、b、c、d分别叫做第一、二、三、四比例项
(2)其中a和d又叫做比例外项,b和c叫做比例内项
(3)在比例式a:b=b:c中,b叫做a和c的比例中项
课后总结3
1、比例的基本性质(小学已学):
(1)如果a:b=c:d,那么ad=bc
(2)反过来,如果ad=bc(b≠0,d≠0),那么a:b=c:d
2、推广:
(1)特别地,如果a:b=b:c,那么ac=b2,即比例外项的积=比例中项的平方
(2)如果ad=bc(a、b、c、d均不为0),那么=,=,=,=
3、比例的其他性质
(1)合比定理:如果=,那么=;分比定理:如果=,那么=
(2)合分比定理:如果=(a-b≠0,c-d≠0),那么=
(3)等比定理:如果=(b±d≠0),那么==
进一步推广:如果===(分母和≠0),那么==
谢谢学习
Thank you for learning
图上距离与实际距离
The distance on the graph and the actual distance
苏科版九年级下册第6章图形的相似
教学目标
01
了解线段的比
02
理解比例尺、成比例线段、比例、比例中项等概念
03
掌握比例的基本性质以及比例的其他性质
两条线段的比
知识精讲
情境引入
01
Q1:两组图中A、B之间有何关系?
A B
A B
【分析】形状相同、大小相等——全等
知识精讲
情境引入
01
Q2:两组图中A、B之间有何关系?
A B
A B
【分析】形状相同、但是大小不等
知识精讲
情境引入
01
Q3:怎样通过具体数值描述出它们的大小关系呢?(以冰墩墩为例)
A B
A B
在冰墩墩A上取两点C、D,连接CD,测量其长度,记为a
在冰墩墩B上取相应的两点C1、D1,连接C1D1,测量其长度,记为b
C
D
C1
D1
两个冰墩墩图形大小的比,即CD:C1D1,即a:b,
因此,要研究形状相同、大小不同的图形,要先研究对应线段(长度)的比
02
知识精讲
两条线段的比
两条线段长度的比,叫做两条线段的比
两条线段的比a:b中,a叫做比的前项,b叫做比的后项
【两条线段的比具有顺序性,要明确前项与后项】
知识精讲
例1、已知AB长为1dm,CD长为2cm,则AB:CD=________.
【分析】
∵AB=1dm=10cm
∴AB:CD=10:2=5:1
【总结】
(1)计算线段的比,即计算线段长度的比
(2)需保证长度的单位统一
【两条线段的比】
知识精讲
例2、如图,画线段AB的垂直平分线交AB于点O,在这条垂直平分线上截取0C=OA,以A为圆心,AC为半径画弧于AB与点P,则线段AP与AB的比是( )
A.:2
B. 1:
C. :
D. :2
【分析】
解:连接AC,
设AO=x,则BO=x,CO=x,
故AC=AP=x,
∴线段AP与AB的比是:x:2x=:2.
D
成比例线段/比例
知识精讲
情境引入
01
在上面两幅比例尺不同的江苏省地图中,设连接南京与徐州的线段长分别为a、b,连接南京与连云港的线段长分别为c、d,问:
(1)比例尺1:8000000与比例尺1:16000000的含义是什么?
(2)a:b与c:d的比值是否相等?
知识精讲
情境引入
01
【分析】(1)∵比例尺=,∴图1:=,图2:=
(1)比例尺1:8000000与比例尺1:16000000的含义是什么?
知识精讲
情境引入
01
(2)a:b与c:d的比值是否相等?
根据比例尺可得:=2=
先度量出a、b、c、d的大小,再分别计算和的值,
可得:=
【分析】(2)
两种方法都可以哦~
02
知识精讲
成比例线段
1、在四条线段中,如果两条线段的比等于另两条线段的比,
那么这四条线段叫做成比例线段,简称比例线段
注意:四条线段成比例时,要把这四条线段按顺序排列,不能随意颠倒
2、比例:两个比相等的式子叫做比例,如 a:b=c:d
(1)比例的四个项a、b、c、d分别叫做第一、二、三、四比例项
(2)其中a和d又叫做比例外项,b和c叫做比例内项
(3)在比例式a:b=b:c中,b叫做a和c的比例中项
02
知识精讲
Q1:下图中,哪两个矩形的长和宽是成比例线段?
9
6
8
4
6
4
(1) (2) (3)
【分析】
∵(1)长:宽=9:6=3:2;(2)长:宽=8:4=2:1;
(3)长:宽=6:4=3:2
∴第1个矩形和第3个矩形的长和宽是成比例线段
02
知识精讲
Q2:如下图,线段A1B1、B1C1、A2B2、B2C2的端点都在边长为1的小正方形的顶点上,问:这四条线段是成比例线段吗?
【分析】
根据题意:
A1B1=2,B1C1=2;A2B2=,B2C2=
将线段按照从小到大的顺序排列:
即A2B2、A1B1、B2C2、B1C1
∵A2B2:A1B1=:2=1:2 ;
B2C2:B1C1=:2=1:2
∴A2B2:A1B1=B2C2:B1C1
∴这四条线段是成比例线段
C2
C1
B1
B2
A1
A2
02
知识精讲
3、判断四条线段是否是成比例线段的方法:
(1)单位统一——确保四条线段的单位统一
(2)排序——将线段按照从小到大的顺序排列
(3)计算——分别计算排序后的前两条线段的比、后两条线段的比
(4)看——看比是否相等
例3-1、在比例尺是1∶10000的地图上,图距25mm,则实距是________m;如果实距为500m,其图距为________cm.
【比例尺问题】
【分析】
∵比例尺=,
∴=,=
∴实际距离=250000mm=250m,图上距离=0.05m=5cm
【注意】切换单位
250
5
例3-2、在比例尺为1∶10000的地图上,一块面积为2cm 的区域表示的实际面积是___________m .
【分析】
∵比例尺==1∶10000,
∴==,
∴实际面积=200000000cm2=20000m2
【注意】
(1)面积比要平方
(2)切换单位again
20000
例4、下列各组中的四条线段成比例的是( )
A.1cm,2cm,3cm,4cm B.1cm,2cm,20cm,40cm
C.4cm,2cm,5cm,3cm D.5cm,10cm,15cm,20cm
【分析】
A.1×4≠2×3,∴四条线段不成比例;
B.1×40=2×20,∴四条线段成比例;
C.排序:2cm,3cm,4cm,5cm,2×5≠3×4,∴四条线段不成比例;
D.5×20≠10×15,∴四条线段不成比例.
【成比例线段的判断】
B
例5-1、线段a=2cm,b=3cm,c=lcm,那么a、b、c的第四比例项d=________.
例5-2、线段a=6cm,b=2cm,则a、b、a+b的第四比例项是________cm.
【比例的有关概念】
【分析5-1】
∵=,
∴=,
∴d=1.5cm
【分析5-2】
设第四比例项为d
∵=,
∴=,
∴d=cm
【注意】单位不能漏
1.5cm
比例的性质
02
知识精讲
1、比例的基本性质(小学已学):
(1)如果a:b=c:d,那么ad=bc
(2)反过来,如果ad=bc(b≠0,d≠0),那么a:b=c:d
2、推广:
(1)特别地,如果a:b=b:c,那么ac=b2,即比例外项的积=比例中项的平方
(2)如果ad=bc(a、b、c、d均不为0),那么=,=,=,=
比例的基本性质
02
知识精讲
Q1:已知=,判断与是否相等
【分析】
∵=,
∴±1=±1,
∴=
合比定理与分比定理
02
知识精讲
Q2:已知=,判断与是否相等
【分析】
设==k(k≠1),则a=kb,c=kd
∴==,==
∴=
合分比定理
【总结】
本问方法为:设“k”法
02
知识精讲
Q3:已知=,判断与是否相等
【分析】
设==k,则a=kb,c=kd
∴==k==
等比定理
【总结】
本问方法也为:设“k”法
02
知识精讲
3、比例的其他性质
(1)合比定理:如果=,那么=
分比定理:如果=,那么=
(2)合分比定理:如果=(a-b≠0,c-d≠0),那么=
比例的其他性质
02
知识精讲
(3)等比定理:如果=(b±d≠0),那么==
进一步推广:
如果===(分母和≠0),那么==
比例的其他性质
例6-1、若a=4cm,b=9cm,则线段a,b的比例中项是________cm.
【比例的基本性质——求比例中项】
【分析】
设比例中项为m
∵ab=m2,
∴(4cm)×(9cm)=m2,
∵m>0
∴m=6cm
6
例6-2、已知三个数3、6、x,要使其中一个数是其他两数的比例中项,则x的取值是____________________________.
【分析】比例中项指代不明,需分类讨论
①设3为比例中项,则6x=32,解得:x=;
②设6为比例中项,则3x=62,解得:x=12;
③设x为比例中项,则3×6=x2,解得:x=;
综上,x=或x=12或x=
x=或x=12或x=
例7、若a:b=3:4,b:c=1:2,则a:c=________.
【分析】
∵a:b=3:4,b:c=1:2=4:8,
∴a:b:c=3:4:8,
∴a:c=3:8
【比例的其他性质】
3:8
【总结】
本题方法:把b转化成同一个数,进行连比
例8、已知=,那么=________.
【分析】
∵=,
∴-1=-1,即=-,
∴=
例9、已知=,那么=________.
【分析】法一:
∵=,
∴a=b,
∴===4
4
法二:
∵=,
∴设a=3k,b=5k,
∴===4
【对比总结】
设“k”法更简单明了
例10、已知a:b:c=9:11:14,且a+b+c=68,则3a-2b+c=________.
【分析】
∵a:b:c=9:11:14,且a+b+c=68,
∴设a=9k,b=11k,c=14k,
∴9k+11k+14k=68,解得:k=2,
∴a=18,b=22,c=28,
∴3a-2b+c=38
38
例11、已知===,且b+d+f≠0,则=________.
【分析】
∵===,且b+d+f≠0,
∴根据等比定理:=
【总结】
直接用设“k”法推导出的等比定理
课后总结1
两条线段长度的比,叫做两条线段的比
两条线段的比a:b中,a叫做比的前项,b叫做比的后项
【两条线段的比具有顺序性,要明确前项与后项】
课后总结2
3、判断四条线段是否是成比例线段的方法:
(1)单位统一——确保四条线段的单位统一
(2)排序——将线段按照从小到大的顺序排列
(3)计算——分别计算排序后的前两条线段的比、后两条线段的比
(4)看——看比是否相等
1、在四条线段中,如果两条线段的比等于另两条线段的比,
那么这四条线段叫做成比例线段,简称比例线段
注意:四条线段成比例时,要把这四条线段按顺序排列,不能随意颠倒
2、比例:两个比相等的式子叫做比例,如 a:b=c:d
(1)比例的四个项a、b、c、d分别叫做第一、二、三、四比例项
(2)其中a和d又叫做比例外项,b和c叫做比例内项
(3)在比例式a:b=b:c中,b叫做a和c的比例中项
课后总结3
1、比例的基本性质(小学已学):
(1)如果a:b=c:d,那么ad=bc
(2)反过来,如果ad=bc(b≠0,d≠0),那么a:b=c:d
2、推广:
(1)特别地,如果a:b=b:c,那么ac=b2,即比例外项的积=比例中项的平方
(2)如果ad=bc(a、b、c、d均不为0),那么=,=,=,=
3、比例的其他性质
(1)合比定理:如果=,那么=;分比定理:如果=,那么=
(2)合分比定理:如果=(a-b≠0,c-d≠0),那么=
(3)等比定理:如果=(b±d≠0),那么==
进一步推广:如果===(分母和≠0),那么==
谢谢学习
Thank you for learning
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
