15.2.2 分式的加减(课件)(共43张PPT)
文档属性
| 名称 | 15.2.2 分式的加减(课件)(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 11:49:31 | ||
图片预览











文档简介
(共43张PPT)
人教版 八年级上册数学
第十五章 分式
15.2.2分式的加减
和分数的计算一样,分式除了乘法和除法,还有加减运算,我们来看下面这道题:
问题1:甲工程队完成一项工程需要n天,乙工程队要比甲队多用3天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?
解:∵甲工程队一天完成这项工程的____,
乙工程队一天完成这项工程的_______ ,
∴两队共同工作一天完成这项工程的 ____________.
问题引入
问题2:2019年、2020年、2021年某地的森林面积 (单位:km2) 分别是S1,S2,S3,2021年与2020年相比,森林面积增长率提高了多少?
∵2021年的森林面积增长率是 ,
2020年的森林面积增长率是 ,
∴2021年与2020年相比,
森林面积增长率提高了 .
解:
从上面的问题可知,为讨论数量关系,有时需要进行分式的加减运算。那么分式的加减运算该怎么计算呢?
①两队共同工作一天完成这项工程的 .
②2021年与2020年相比,
森林面积增长率提高了 .
在探索未知事物的时候,我们常用到类比法,将未知与已知进行类比,找出异同点,探索出解决未知的办法。
这一次我们依旧与分数的加减进行类比,我们先回忆一下,分数是如何加减的?
1、同分母分数相加减
例如:
分母相同时,分母不变,只把分子相加减;
一、同分母分式的加减法则
所以同分母分数相加减相同
同分母的分式加减法的法则
同分母分式相加减,分母不变,把分子相加减.
例1 计算:
解:原式
归纳总结:
同分母分式的加减,分母不变,分子相加减,当分子是多项式时,先加括号,然后进行计算,结果要化为最简分式或整式.
–1
1.直接说出运算结果.
(1)
(2)
(3)
(4)
2.计算:
解:原式
解:原式
(1)
(2)
1、异分母分数相加减
例如:
分母不同时,要先通分成同分母的分数,再加减.;
二、异分母分式的加减法则
所以异分母分数相加减相同
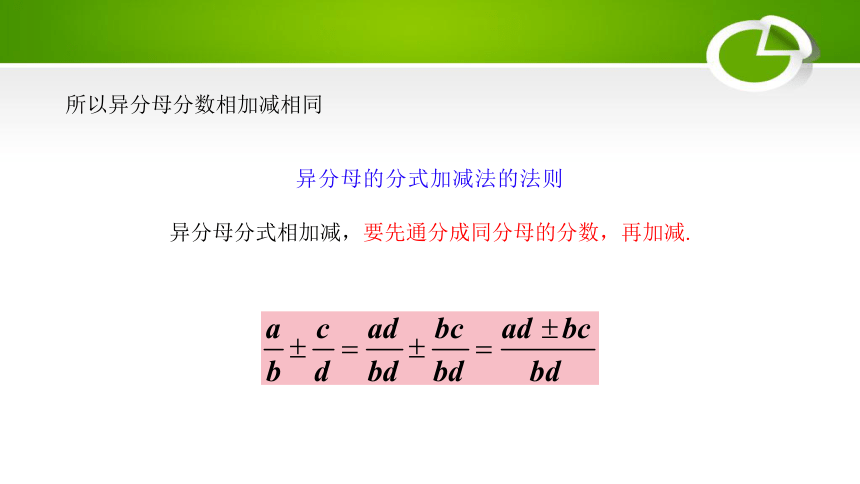
异分母的分式加减法的法则
异分母分式相加减,要先通分成同分母的分数,再加减.
例2 (1)
解:原式
归纳总结:
异分母分式的加减分为两步:第一步通分,化为同分母分式;第二步运用同分母分式的加减法则计算.
(2)
解:原式
分析:
∵a2 –4 =(a+2)(a–2),
其中 (a–2)恰好为第二个分式的分母,所以 (a+2)(a–2)即为最简公分母.
易错点:分子相减时,“减式”为多项式时要添括号!
归纳小结
(1)异分母分式加减运算的关键是通分,再根据同分母分式的加减法法则进行计算.
(2)通分前要将能分解因式的分母分解因式,通分时更容易确定最简公分母.
3.计算:
=x+y
解:原式
=
解:原式
(1)
(2)
解:原式=
易错点:减式为整式且第一项为负时,一般先提取负号,再将括号内的部分作为分母为1的分数的分子,然后按照异分母分式加减进行计算。
解:原式=
1.填空:
4
练一练
2.计算:
解:(1)原式=
(2)原式=
3.先化简,再求值:: ,其中x=2016.
分式的加减
同分母分式相加减
异分母分式相加减
分母不变,把分子相加减
先通分,变为同分母的分式,再加减
同分母加减:
异分母加减:
分式的运算法则
乘法:
除法:
加减法
乘方:
分式的混合运算
互动探究:分式的混合运算
问题:如何计算 ?
请先思考这道题包含的运算,确定运算顺序,再独立完成.
解:
先乘方,再乘除,最后加减
知识要点
分式的混合运算顺序
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
计算结果要化为最简分式或整式.
例1 计算:
解:原式
先算括号里的加法,再算括号外的乘法
注:当式子中出现整式时,把整式看成整体,并把分母看做“1”
或
解:原式
注意:分子或分母是多项式的先因式分解,不能分解的要视为整体.
练一练
解:原式
计算:
解:原式
方法总结:观察题目的结构特点,灵活运用运算律,适当运用计算技巧,可简化运算,提高速度.
例2 计算:
利用乘法分配率简化运算
用两种方法计算:
=
解:(按运算顺序)
原式
=
做一做
解:(利用乘法分配律)
原式
例3:计算
分析:把 和 看成整体,题目的实质是平方
差公式的应用.
解:原式
巧用公式
例4:先化简,再求值: 再从
-4<x<4的范围内选取一个合适的整数x代入求值.
解析:先计算括号里的减法运算,再把除法运算转化成乘法运算,进行约分化简,最后从x的取值范围内选取一数值代入即可.
方法总结:把分式化成最简分式是解题的关键,通分、因式分解和约分是基本环节,注意选数时,要求分母不能为0.
【归纳总结】有关分式化简求值的解题模板
解题步骤 解题注意事项
第一步,将所给分式化为最简分式或整式 正确应用运算法则
第二步,根据条件求出未知数的值 有的可以求出具体值,对于求不出的可考虑整体代入
第三步,将未知数的值代入化简后的式子 要检验未知数的值,使原分式有意义的数值才能代入
1.(2020·黄冈中考)计算: 的结果是____.
课堂练习
2.计算: .
解:原式
解:原式
3.计算: .
4.计算: .
解:原式
提示:将待化简的式子按照分式的混合运算法则进行计算,然后解不等式组得到x的取值范围,在选取整数解时要注意满足分式有意义的条件,否则不能选取该整数.
解:原式 ,
分式的混合运算
分式的混合运算
熟练运用分式的混合运算法则进行计算
先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
课堂小结
人教版 八年级上册数学
第十五章 分式
15.2.2分式的加减
和分数的计算一样,分式除了乘法和除法,还有加减运算,我们来看下面这道题:
问题1:甲工程队完成一项工程需要n天,乙工程队要比甲队多用3天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?
解:∵甲工程队一天完成这项工程的____,
乙工程队一天完成这项工程的_______ ,
∴两队共同工作一天完成这项工程的 ____________.
问题引入
问题2:2019年、2020年、2021年某地的森林面积 (单位:km2) 分别是S1,S2,S3,2021年与2020年相比,森林面积增长率提高了多少?
∵2021年的森林面积增长率是 ,
2020年的森林面积增长率是 ,
∴2021年与2020年相比,
森林面积增长率提高了 .
解:
从上面的问题可知,为讨论数量关系,有时需要进行分式的加减运算。那么分式的加减运算该怎么计算呢?
①两队共同工作一天完成这项工程的 .
②2021年与2020年相比,
森林面积增长率提高了 .
在探索未知事物的时候,我们常用到类比法,将未知与已知进行类比,找出异同点,探索出解决未知的办法。
这一次我们依旧与分数的加减进行类比,我们先回忆一下,分数是如何加减的?
1、同分母分数相加减
例如:
分母相同时,分母不变,只把分子相加减;
一、同分母分式的加减法则
所以同分母分数相加减相同
同分母的分式加减法的法则
同分母分式相加减,分母不变,把分子相加减.
例1 计算:
解:原式
归纳总结:
同分母分式的加减,分母不变,分子相加减,当分子是多项式时,先加括号,然后进行计算,结果要化为最简分式或整式.
–1
1.直接说出运算结果.
(1)
(2)
(3)
(4)
2.计算:
解:原式
解:原式
(1)
(2)
1、异分母分数相加减
例如:
分母不同时,要先通分成同分母的分数,再加减.;
二、异分母分式的加减法则
所以异分母分数相加减相同
异分母的分式加减法的法则
异分母分式相加减,要先通分成同分母的分数,再加减.
例2 (1)
解:原式
归纳总结:
异分母分式的加减分为两步:第一步通分,化为同分母分式;第二步运用同分母分式的加减法则计算.
(2)
解:原式
分析:
∵a2 –4 =(a+2)(a–2),
其中 (a–2)恰好为第二个分式的分母,所以 (a+2)(a–2)即为最简公分母.
易错点:分子相减时,“减式”为多项式时要添括号!
归纳小结
(1)异分母分式加减运算的关键是通分,再根据同分母分式的加减法法则进行计算.
(2)通分前要将能分解因式的分母分解因式,通分时更容易确定最简公分母.
3.计算:
=x+y
解:原式
=
解:原式
(1)
(2)
解:原式=
易错点:减式为整式且第一项为负时,一般先提取负号,再将括号内的部分作为分母为1的分数的分子,然后按照异分母分式加减进行计算。
解:原式=
1.填空:
4
练一练
2.计算:
解:(1)原式=
(2)原式=
3.先化简,再求值:: ,其中x=2016.
分式的加减
同分母分式相加减
异分母分式相加减
分母不变,把分子相加减
先通分,变为同分母的分式,再加减
同分母加减:
异分母加减:
分式的运算法则
乘法:
除法:
加减法
乘方:
分式的混合运算
互动探究:分式的混合运算
问题:如何计算 ?
请先思考这道题包含的运算,确定运算顺序,再独立完成.
解:
先乘方,再乘除,最后加减
知识要点
分式的混合运算顺序
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
计算结果要化为最简分式或整式.
例1 计算:
解:原式
先算括号里的加法,再算括号外的乘法
注:当式子中出现整式时,把整式看成整体,并把分母看做“1”
或
解:原式
注意:分子或分母是多项式的先因式分解,不能分解的要视为整体.
练一练
解:原式
计算:
解:原式
方法总结:观察题目的结构特点,灵活运用运算律,适当运用计算技巧,可简化运算,提高速度.
例2 计算:
利用乘法分配率简化运算
用两种方法计算:
=
解:(按运算顺序)
原式
=
做一做
解:(利用乘法分配律)
原式
例3:计算
分析:把 和 看成整体,题目的实质是平方
差公式的应用.
解:原式
巧用公式
例4:先化简,再求值: 再从
-4<x<4的范围内选取一个合适的整数x代入求值.
解析:先计算括号里的减法运算,再把除法运算转化成乘法运算,进行约分化简,最后从x的取值范围内选取一数值代入即可.
方法总结:把分式化成最简分式是解题的关键,通分、因式分解和约分是基本环节,注意选数时,要求分母不能为0.
【归纳总结】有关分式化简求值的解题模板
解题步骤 解题注意事项
第一步,将所给分式化为最简分式或整式 正确应用运算法则
第二步,根据条件求出未知数的值 有的可以求出具体值,对于求不出的可考虑整体代入
第三步,将未知数的值代入化简后的式子 要检验未知数的值,使原分式有意义的数值才能代入
1.(2020·黄冈中考)计算: 的结果是____.
课堂练习
2.计算: .
解:原式
解:原式
3.计算: .
4.计算: .
解:原式
提示:将待化简的式子按照分式的混合运算法则进行计算,然后解不等式组得到x的取值范围,在选取整数解时要注意满足分式有意义的条件,否则不能选取该整数.
解:原式 ,
分式的混合运算
分式的混合运算
熟练运用分式的混合运算法则进行计算
先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
课堂小结
