28.1.2 余弦、正切课件(共24张PPT)
文档属性
| 名称 | 28.1.2 余弦、正切课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 13:30:06 | ||
图片预览




文档简介
(共24张PPT)
余弦、正切
1. 认识并理解余弦、正切的概念进而得到锐角三角函数的概念.(重点)
2. 能灵活运用锐角三角函数进行相关运算.(重点、难点)
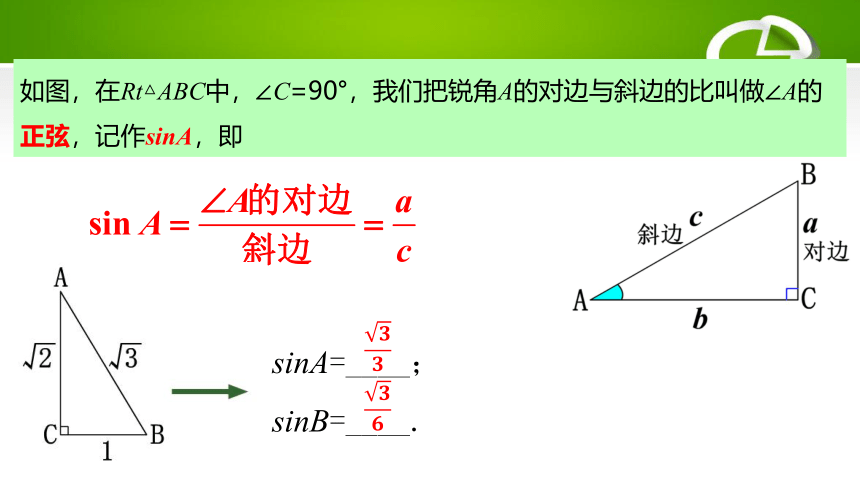
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即
sinA=____;
sinB=____.
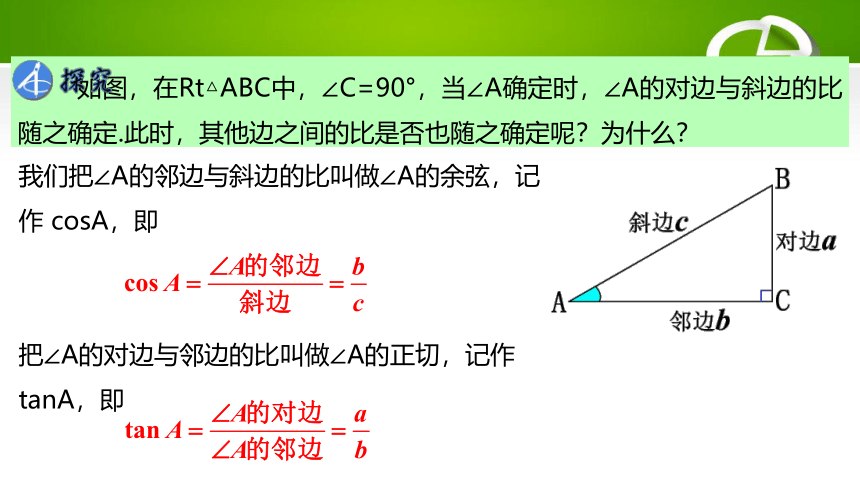
如图,在Rt△ABC中,∠C=90°,当∠A确定时,∠A的对边与斜边的比随之确定.此时,其他边之间的比是否也随之确定呢?为什么?
我们把∠A的邻边与斜边的比叫做∠A的余弦,记作 cosA,即
把∠A的对边与邻边的比叫做∠A的正切,记作tanA,即
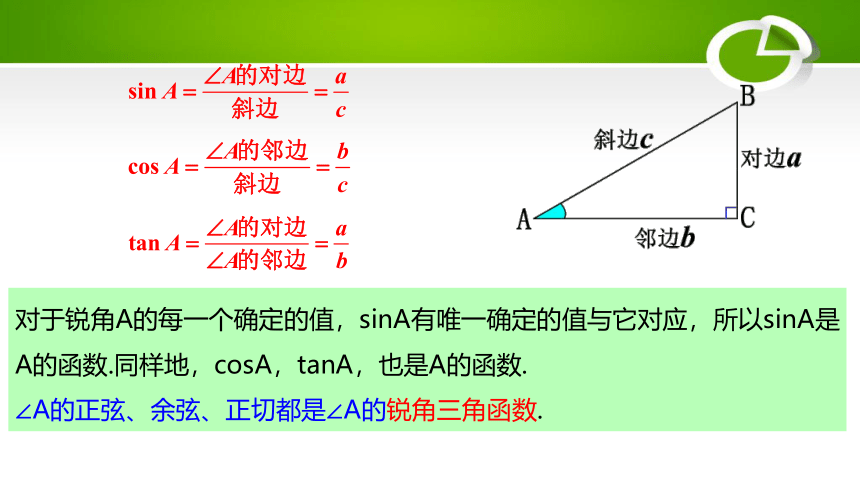
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,cosA,tanA,也是A的函数.
∠A的正弦、余弦、正切都是∠A的锐角三角函数.
例2.如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
解:由勾股定理得
因此sinA= ,
cosA= ,
tanA= .
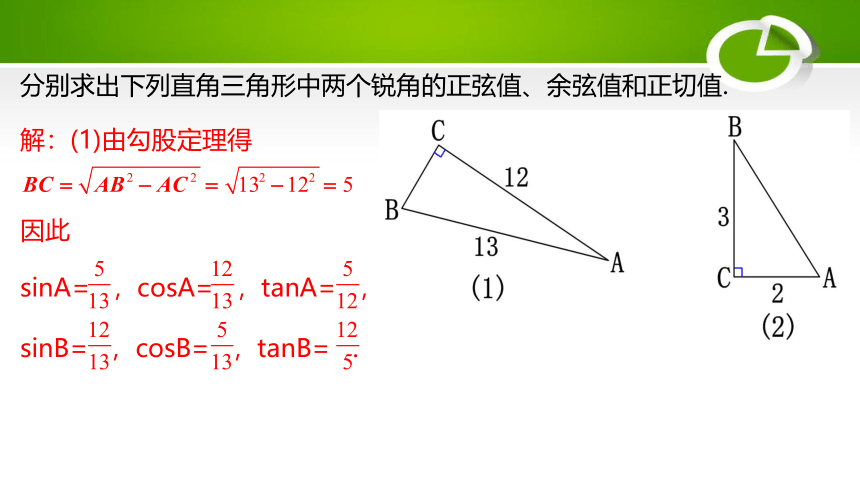
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
解:(1)由勾股定理得
因此
sinA= ,cosA= ,tanA= ,
sinB= ,cosB= ,tanB= .
观察(1)中两锐角的三角函数值,你有什么新发现?
解:(1)由勾股定理得
因此
sinA= ,cosA= ,tanA= ,
sinB= ,cosB= ,tanB= .
Ⅰ.对于任意锐角α,有sinα=cos(90°-α), cos α = sin (90°-α).
Ⅱ.如果两个角互余,那么这两个角的正切值互为倒数.
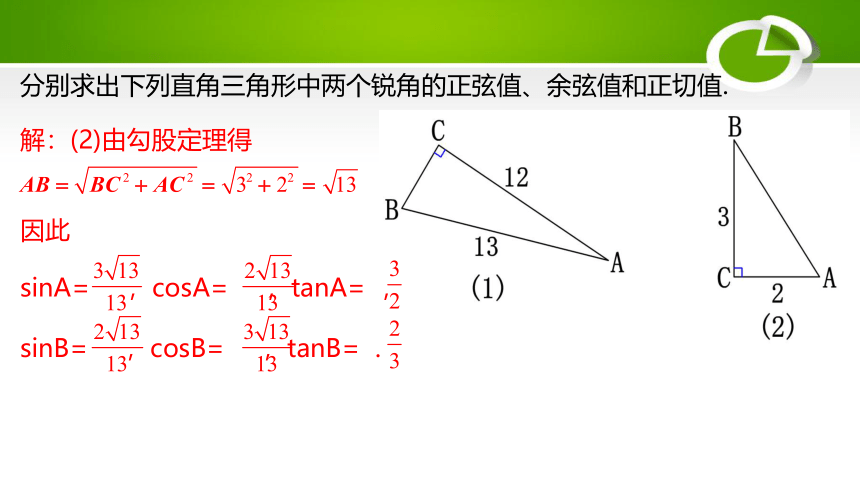
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
解:(2)由勾股定理得
因此
sinA= ,cosA= ,tanA= ,
sinB= ,cosB= ,tanB= .
A
B
C
6
例2.如图,在Rt△ABC中,∠C=90°,BC=6, sinA= ,求cosA、tanB的值.
解:∵
又
∴
【点睛】在直角三角形中,如果已知一边长及一个锐角的某个三角函数值,即可求出其它的所有锐角三角函数值
A
B
C
8
解:∵
如图,在Rt△ABC中,∠C=90°,AC=8,tanA= , 求sinA,cosB 的值.
∴
∴
∴
例3.如图,已知中,,,,边的垂直平分线分别交、于点、.求线段的长.
解:过A作,垂足为点H,如图所示:
在中,,,
∴,,
在中,,
∴,
∴,
∵垂直平分,
∴,,
例3.如图,已知中,,,,边的垂直平分线分别交、于点、.求线段的长.
在中,,
∴,
∴.
如图,在△ABC中,AD上BC于点D,若AD=6,BC=12,tanC=,求:
(1)CD的长
(2)cosB的值
(1)解:∵AD⊥BC,
∴∠ADC=90°,
∵在Rt△ADC中,,
∴;
(2)解:由(1)得CD=4,
∴BD=BC-CD=8,
在Rt△ABD中,由勾股定理得:,
∴.
1.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,则下列关系式正确的是( )
A.b=a·tanA B.b=c·sinA C.a=c·cosB D.c=a·sinA
2.在Rt△ABC中,∠C=90°,AB=4,AC=1,则cosA的值是( )
A.4 B. C. D.
C
B
3.如图,直径为10的☉A经过点C(0,5)和点0(0,0),B是y轴右侧☉A优弧上一点,则∠OBC的余弦值为( )
A. B. C. D.
C
4.如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于( )
A. B. C. D.
B
5.如图,在△ABC中,CA=CB=4,cosC=,则sinB的值为( )
A. B. C. D.
D
6.在Rt△ABC中,∠C=90°,AC=5,BC=4,则tanA=_____.
7.在Rt△ABC中,AB是斜边,AB=,BC=,则cosA=_____.
8.在Rt△ABC中,∠C=90°,tanA=,BC=8,则S△ABC=_____.
9.在Rt△ABC中,∠C=90°,tanA=1,,则sinB=_____.
10.如图,边长为1的小正方形构成的网格中,半径为1的圆的圆心O在格点上,则∠AED的正切值等于_______.
11.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,AD=2BC,AC与BD交于点E,
AC⊥BD,则tan∠BAC的值等于______.
12.如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别是a、b、c,且b=8,c=17.求: sinA、 cosA、 tanA、 sinB、cosB、 tanB.
解:由勾股定理得
因此sinA= cosA= ,tanA= ,
sinB= ,cosB= ,tanB= .
13.如图,在等腰△ABC中,AB=AC, 若AB=2BC,试求∠B的正弦值和正切值.
解:过A作AD⊥BC于D
∵AB=AC,AB=2BC
∴BD=DC=BC=AB
设BD=DC=k,则BC=2k,AB=4k
由勾股定理得
因此,
sinB= ,tanB=
14.如图,在△ABC中,D是AB的中点,DC⊥AC,且tan∠BCD=,求sinA、
cosA、tanA的值.
解:过D作DE⊥DC交BC于E.
在Rt△CDE中tan∠BCD==
可设DE=k,则CD=3k
∵DC⊥AC ∴DE∥AC
∵D为AB中点 ∴E为BC中点∴AC=2DE=2k
∴AD==k
∴sinA==,cosA=,tanA=.
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,cosA,tanA,也是A的函数.
∠A的正弦、余弦、正切都是∠A的锐角三角函数.
余弦、正切
1. 认识并理解余弦、正切的概念进而得到锐角三角函数的概念.(重点)
2. 能灵活运用锐角三角函数进行相关运算.(重点、难点)
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即
sinA=____;
sinB=____.
如图,在Rt△ABC中,∠C=90°,当∠A确定时,∠A的对边与斜边的比随之确定.此时,其他边之间的比是否也随之确定呢?为什么?
我们把∠A的邻边与斜边的比叫做∠A的余弦,记作 cosA,即
把∠A的对边与邻边的比叫做∠A的正切,记作tanA,即
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,cosA,tanA,也是A的函数.
∠A的正弦、余弦、正切都是∠A的锐角三角函数.
例2.如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
解:由勾股定理得
因此sinA= ,
cosA= ,
tanA= .
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
解:(1)由勾股定理得
因此
sinA= ,cosA= ,tanA= ,
sinB= ,cosB= ,tanB= .
观察(1)中两锐角的三角函数值,你有什么新发现?
解:(1)由勾股定理得
因此
sinA= ,cosA= ,tanA= ,
sinB= ,cosB= ,tanB= .
Ⅰ.对于任意锐角α,有sinα=cos(90°-α), cos α = sin (90°-α).
Ⅱ.如果两个角互余,那么这两个角的正切值互为倒数.
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
解:(2)由勾股定理得
因此
sinA= ,cosA= ,tanA= ,
sinB= ,cosB= ,tanB= .
A
B
C
6
例2.如图,在Rt△ABC中,∠C=90°,BC=6, sinA= ,求cosA、tanB的值.
解:∵
又
∴
【点睛】在直角三角形中,如果已知一边长及一个锐角的某个三角函数值,即可求出其它的所有锐角三角函数值
A
B
C
8
解:∵
如图,在Rt△ABC中,∠C=90°,AC=8,tanA= , 求sinA,cosB 的值.
∴
∴
∴
例3.如图,已知中,,,,边的垂直平分线分别交、于点、.求线段的长.
解:过A作,垂足为点H,如图所示:
在中,,,
∴,,
在中,,
∴,
∴,
∵垂直平分,
∴,,
例3.如图,已知中,,,,边的垂直平分线分别交、于点、.求线段的长.
在中,,
∴,
∴.
如图,在△ABC中,AD上BC于点D,若AD=6,BC=12,tanC=,求:
(1)CD的长
(2)cosB的值
(1)解:∵AD⊥BC,
∴∠ADC=90°,
∵在Rt△ADC中,,
∴;
(2)解:由(1)得CD=4,
∴BD=BC-CD=8,
在Rt△ABD中,由勾股定理得:,
∴.
1.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,则下列关系式正确的是( )
A.b=a·tanA B.b=c·sinA C.a=c·cosB D.c=a·sinA
2.在Rt△ABC中,∠C=90°,AB=4,AC=1,则cosA的值是( )
A.4 B. C. D.
C
B
3.如图,直径为10的☉A经过点C(0,5)和点0(0,0),B是y轴右侧☉A优弧上一点,则∠OBC的余弦值为( )
A. B. C. D.
C
4.如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于( )
A. B. C. D.
B
5.如图,在△ABC中,CA=CB=4,cosC=,则sinB的值为( )
A. B. C. D.
D
6.在Rt△ABC中,∠C=90°,AC=5,BC=4,则tanA=_____.
7.在Rt△ABC中,AB是斜边,AB=,BC=,则cosA=_____.
8.在Rt△ABC中,∠C=90°,tanA=,BC=8,则S△ABC=_____.
9.在Rt△ABC中,∠C=90°,tanA=1,,则sinB=_____.
10.如图,边长为1的小正方形构成的网格中,半径为1的圆的圆心O在格点上,则∠AED的正切值等于_______.
11.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,AD=2BC,AC与BD交于点E,
AC⊥BD,则tan∠BAC的值等于______.
12.如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别是a、b、c,且b=8,c=17.求: sinA、 cosA、 tanA、 sinB、cosB、 tanB.
解:由勾股定理得
因此sinA= cosA= ,tanA= ,
sinB= ,cosB= ,tanB= .
13.如图,在等腰△ABC中,AB=AC, 若AB=2BC,试求∠B的正弦值和正切值.
解:过A作AD⊥BC于D
∵AB=AC,AB=2BC
∴BD=DC=BC=AB
设BD=DC=k,则BC=2k,AB=4k
由勾股定理得
因此,
sinB= ,tanB=
14.如图,在△ABC中,D是AB的中点,DC⊥AC,且tan∠BCD=,求sinA、
cosA、tanA的值.
解:过D作DE⊥DC交BC于E.
在Rt△CDE中tan∠BCD==
可设DE=k,则CD=3k
∵DC⊥AC ∴DE∥AC
∵D为AB中点 ∴E为BC中点∴AC=2DE=2k
∴AD==k
∴sinA==,cosA=,tanA=.
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,cosA,tanA,也是A的函数.
∠A的正弦、余弦、正切都是∠A的锐角三角函数.
