28.1.3 特殊角的三角函数值课件(共23张PPT)
文档属性
| 名称 | 28.1.3 特殊角的三角函数值课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 13:32:10 | ||
图片预览





文档简介
(共23张PPT)
特殊角的三角函数值
1.运用三角函数的知识,自主探索,推导出30°、45°、60°角的三角函数值.(重点)
2.熟记三个特殊锐角的三角函数值,并能准确地加以运用.(难点)
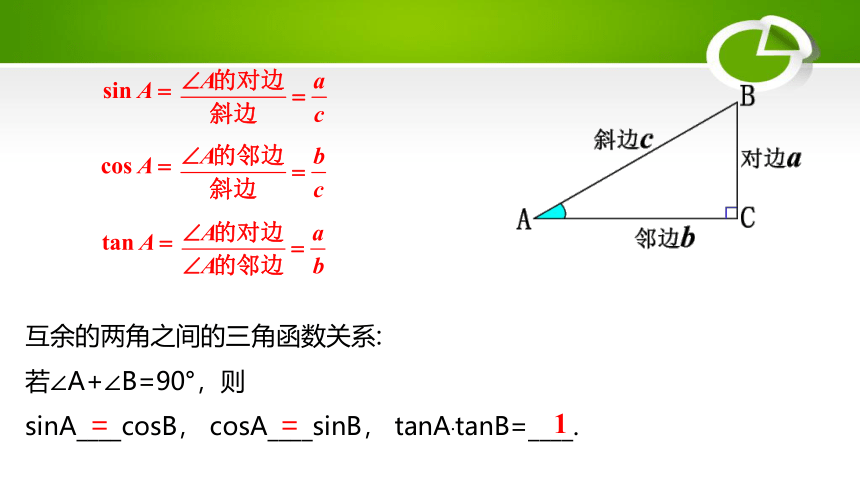
互余的两角之间的三角函数关系:
若∠A+∠B=90°,则
sinA____cosB, cosA____sinB, tanA·tanB=____.
=
=
1
1.如图,在Rt△ABC中,∠C=90°,AB=0.5,AC=0.3,则cosA=____,sinB=____,tanB=____.
2.在Rt△ABC中,∠C=90°,若tanA=,AC=6,则BC=____,AB=______.
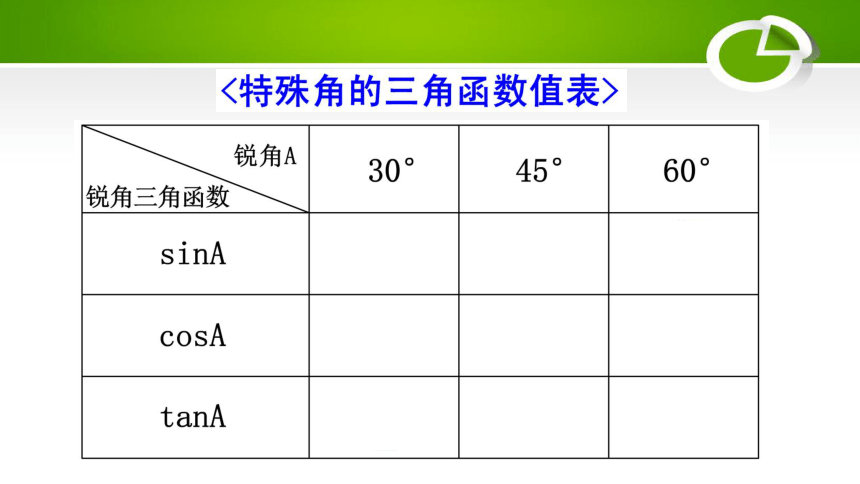
两块三角尺中有几个不同的锐角?这几个锐角的正弦值、余弦值和正切值各是多少?
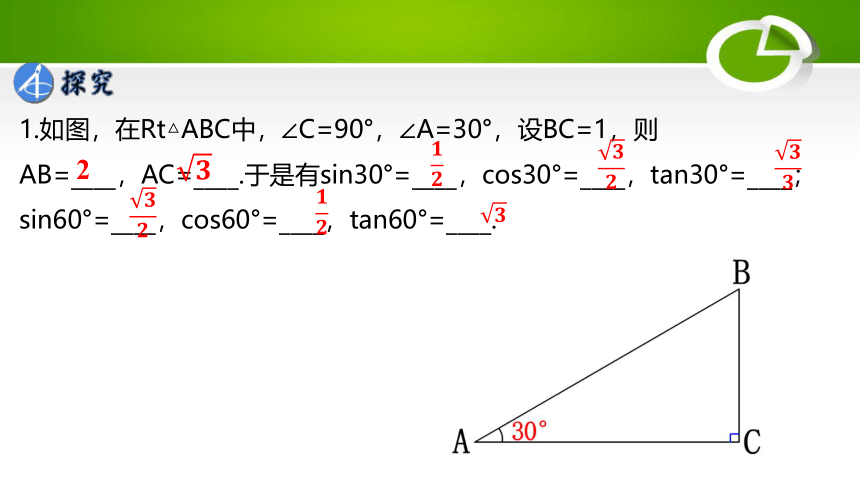
1.如图,在Rt△ABC中,∠C=90°,∠A=30°,设BC=1,则
AB=____,AC=____.于是有sin30°=____,cos30°=____,tan30°=____;sin60°=____,cos60°=____,tan60°=____.
2
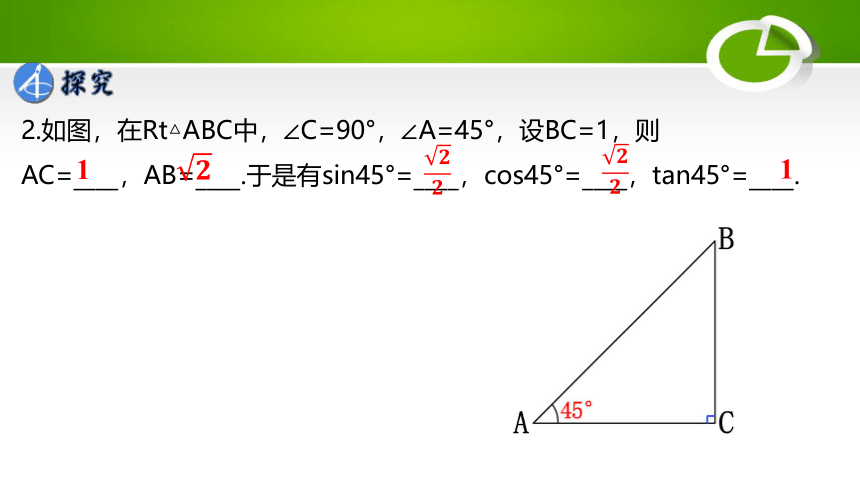
2.如图,在Rt△ABC中,∠C=90°,∠A=45°,设BC=1,则
AC=____,AB=____.于是有sin45°=____,cos45°=____,tan45°=____.
1
1
例1.求下列各式的值:
(1) (2)
解:(1)原式
(2)原式
求下列各式的值:
(1)1-2sin30°cos30° (2)3tan30°-tan45°+2sin60°
(3)(cos230°+sin230°)×tan60°
解:(1)原式
(3)原式
(2)原式
解:在图中,
例2.(1)如图,在Rt△ABC中,∠C=90°,AB= , BC= ,求∠A的度数.
∴∠A = 45°
∵
解:在图中,
∴ α = 60°
∵ tanα =
例2.(2)如图,AO是圆锥的高,OB是底面半径,AO= OB,求α的度数.
在Rt△ABC中,∠C=90°,BC=,AC=,求∠A,∠B的度数.
解:如图,∵ tanB=
∴ ∠B=60°
∴ ∠A=90°-∠B=30°
例3.已知中,都是锐角,且,
(1)分别求出三个内角度数;
(2)若,求长度.
(1)解:
,
,
,
;
例3.已知中,都是锐角,且,
(2)若,求长度.
(2)解:如图:过点C作于点D
,
,
.
已知△ABC中的∠A与∠B满足(1-tanA)2 +|sinB- |=0,试判断△ABC的形状.
解:∵ (1-tanA)2 + |sinB- |=0,
∴ tanA=1,sinB=
∴ ∠A=45°,∠B=60°,
∠C=180°-45°-60°=75°,
∴ △ABC 是锐角三角形.
1.2sin45°的值等于( )
A.1 B. C. D.2
2.Rt△ABC中,∠C=90°,∠A:∠B=1:2,则tanA的值( )
A. B. C. D.
3.在△ABC中,若cosA=,tanB=,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
B
C
A
4.在△ABC中,若+(cosB-)2=0,则∠C为( )
A.30° B.45° C.60° D.90°
5.按如图所示的运算程序,能使输出y值为一的是( )
a=600β=45° B.a=300β=45°
C.a=30°β =60° D.a=60β =60°
D
C
6.计算:cos45°=______.
7.计算 的值是_______.
8.已知2sina-=0,则锐角a=______.
9.化简: =_______.
10.在△ABC中,若|2cosA-1|+(tanB-1)2=0,则∠C=_____.
11.如图,在△ABC中,∠C=90°,tan∠ABC=,BD平分∠ABC,若AD=6,则CD=_____.
1
0
60°
2-
75°
3
12.计算:
(1) sin30°+cos30°tan60° (2) (2cos45°-sin60°)+
(3) 2sin260°-tan30°-2cos245°
解:(1)原式=×=+=2
(2)原式=(-)+=2-+=2
(3)原式=2×-1-2×=-1-1=-
13.如图,△ABC内接于☉O,点D在OC的延长线上,sinB=,∠D=30°,求证: AD是☉O的切线.
证明:连接0A.
∵sinB=
∴∠B=30°
∵
∴∠COA=2∠B=60°
又∠D=30°
∴∠OAD=180°- 60°-30°=90°
∴AD是O0的切线
14.如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.求证: sin2A+cos2A=1.
证明:∵sinA=,cosA= ∴sin2A+cos2A=+=+=
由勾股定理可知,a2+b2=c2
∴sin2A+cos2A=1
特殊角的三角函数值
1.运用三角函数的知识,自主探索,推导出30°、45°、60°角的三角函数值.(重点)
2.熟记三个特殊锐角的三角函数值,并能准确地加以运用.(难点)
互余的两角之间的三角函数关系:
若∠A+∠B=90°,则
sinA____cosB, cosA____sinB, tanA·tanB=____.
=
=
1
1.如图,在Rt△ABC中,∠C=90°,AB=0.5,AC=0.3,则cosA=____,sinB=____,tanB=____.
2.在Rt△ABC中,∠C=90°,若tanA=,AC=6,则BC=____,AB=______.
两块三角尺中有几个不同的锐角?这几个锐角的正弦值、余弦值和正切值各是多少?
1.如图,在Rt△ABC中,∠C=90°,∠A=30°,设BC=1,则
AB=____,AC=____.于是有sin30°=____,cos30°=____,tan30°=____;sin60°=____,cos60°=____,tan60°=____.
2
2.如图,在Rt△ABC中,∠C=90°,∠A=45°,设BC=1,则
AC=____,AB=____.于是有sin45°=____,cos45°=____,tan45°=____.
1
1
例1.求下列各式的值:
(1) (2)
解:(1)原式
(2)原式
求下列各式的值:
(1)1-2sin30°cos30° (2)3tan30°-tan45°+2sin60°
(3)(cos230°+sin230°)×tan60°
解:(1)原式
(3)原式
(2)原式
解:在图中,
例2.(1)如图,在Rt△ABC中,∠C=90°,AB= , BC= ,求∠A的度数.
∴∠A = 45°
∵
解:在图中,
∴ α = 60°
∵ tanα =
例2.(2)如图,AO是圆锥的高,OB是底面半径,AO= OB,求α的度数.
在Rt△ABC中,∠C=90°,BC=,AC=,求∠A,∠B的度数.
解:如图,∵ tanB=
∴ ∠B=60°
∴ ∠A=90°-∠B=30°
例3.已知中,都是锐角,且,
(1)分别求出三个内角度数;
(2)若,求长度.
(1)解:
,
,
,
;
例3.已知中,都是锐角,且,
(2)若,求长度.
(2)解:如图:过点C作于点D
,
,
.
已知△ABC中的∠A与∠B满足(1-tanA)2 +|sinB- |=0,试判断△ABC的形状.
解:∵ (1-tanA)2 + |sinB- |=0,
∴ tanA=1,sinB=
∴ ∠A=45°,∠B=60°,
∠C=180°-45°-60°=75°,
∴ △ABC 是锐角三角形.
1.2sin45°的值等于( )
A.1 B. C. D.2
2.Rt△ABC中,∠C=90°,∠A:∠B=1:2,则tanA的值( )
A. B. C. D.
3.在△ABC中,若cosA=,tanB=,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
B
C
A
4.在△ABC中,若+(cosB-)2=0,则∠C为( )
A.30° B.45° C.60° D.90°
5.按如图所示的运算程序,能使输出y值为一的是( )
a=600β=45° B.a=300β=45°
C.a=30°β =60° D.a=60β =60°
D
C
6.计算:cos45°=______.
7.计算 的值是_______.
8.已知2sina-=0,则锐角a=______.
9.化简: =_______.
10.在△ABC中,若|2cosA-1|+(tanB-1)2=0,则∠C=_____.
11.如图,在△ABC中,∠C=90°,tan∠ABC=,BD平分∠ABC,若AD=6,则CD=_____.
1
0
60°
2-
75°
3
12.计算:
(1) sin30°+cos30°tan60° (2) (2cos45°-sin60°)+
(3) 2sin260°-tan30°-2cos245°
解:(1)原式=×=+=2
(2)原式=(-)+=2-+=2
(3)原式=2×-1-2×=-1-1=-
13.如图,△ABC内接于☉O,点D在OC的延长线上,sinB=,∠D=30°,求证: AD是☉O的切线.
证明:连接0A.
∵sinB=
∴∠B=30°
∵
∴∠COA=2∠B=60°
又∠D=30°
∴∠OAD=180°- 60°-30°=90°
∴AD是O0的切线
14.如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.求证: sin2A+cos2A=1.
证明:∵sinA=,cosA= ∴sin2A+cos2A=+=+=
由勾股定理可知,a2+b2=c2
∴sin2A+cos2A=1
