28.2.1 解直角三角形课件(共26张PPT)
文档属性
| 名称 | 28.2.1 解直角三角形课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
解直角三角形
1. 了解并掌握解直角三角形的概念;
2. 理解直角三角形中的五个元素之间的联系. (重点)
3. 学会解直角三角形. (难点)
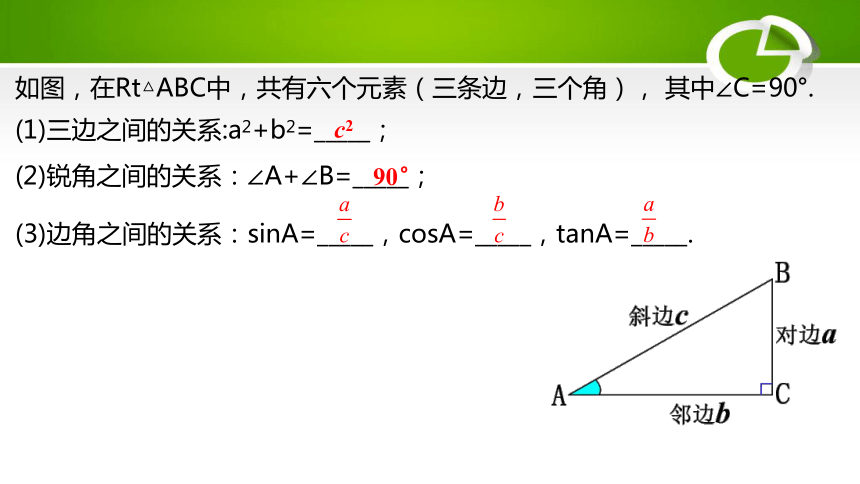
(1)三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
如图,在Rt△ABC中,共有六个元素(三条边,三个角), 其中∠C=90°.
c2
90°
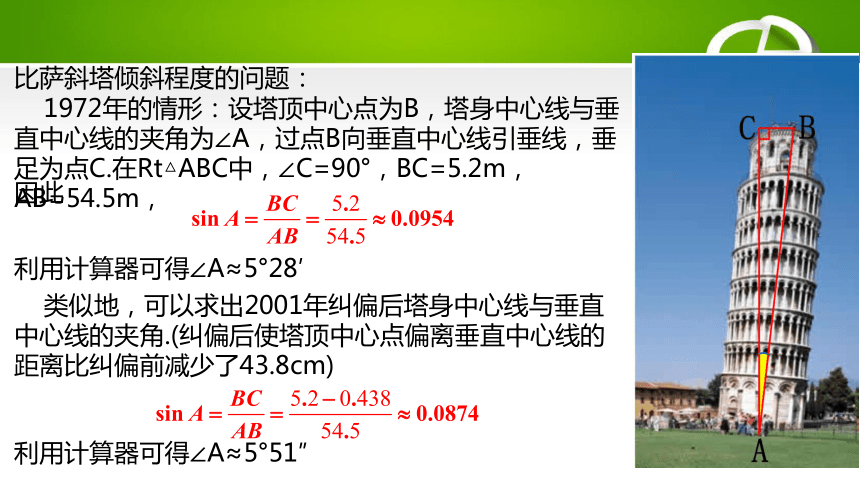
比萨斜塔倾斜程度的问题:
1972年的情形:设塔顶中心点为B,塔身中心线与垂
直中心线的夹角为∠A,过点B向垂直中心线引垂线,垂
足为点C.在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m,
因此
利用计算器可得∠A≈5°28′
类似地,可以求出2001年纠偏后塔身中心线与垂直中心线的夹角.(纠偏后使塔顶中心点偏离垂直中心线的距离比纠偏前减少了43.8cm)
利用计算器可得∠A≈5°51″
比萨斜塔倾斜程度的问题:
1972年的情形:设塔顶中心点为B,塔身中心线与垂
直中心线的夹角为∠A,过点B向垂直中心线引垂线,垂
足为点C.在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m,
因此
利用计算器可得∠A≈5°28′
如果将上述实际问题抽象为数学问题,就是已知直角三角形的斜边和一条直角边,求它的锐角的度数.
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角. 由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
(1)在直角三角形中,除直角外的五个元素之间有哪些关系? (2)知道五个元素中的几个,就可以求其余元素?
(1)三边之间的关系
(2)两锐角之间的关系
(3)边角之间的关系
∠A+∠B=90°
a2+b2=c2(勾股定理)
(3)中的A都可以换成B,同时把a,b互换.
利用这些关系,知道其中的两个元素(至少有一个是边),就可以求出其余三个未知元素.
例1.如图,在Rt△ABC中,∠C=90°,AC=,BC=,解这个直角三角形.
解:∵
∴ ∠A=60°
∠B=90°-∠A=90°-60°=30°
AB=2AC=2
在Rt△ABC中,∠C=90°,a=30,b=20,根据条件解直角三角形.
解:根据勾股定理
例2.如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形(结果保留小数点后一位).
解:
在Rt△ABC中,∠C=90°,∠B=72°,c=14.根据条件解直角三角形.
解:
例3.如图,在△ABC中,sinB=,,AC=5,则△ABC的面积为多少?
D
解:过点A作AD⊥BC,垂足为D.
在RtΔACD中,, AC=5,
∴CD=ACcosC=5=4.
∴由勾股定理得:AD==3.
∵sinB=,
∴∠B=45°.
∴∠BAD=∠B=45°.
∴BD=AD=3.
∴S△ABC=BC AD=(3+4)×3=10.5.
如图,△ABC中,AB=12,BC=15,∠ABC=60°.求tanC的值.
D
解:过点A作AD⊥BC于点D,如图所示:
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵△ABC中,AB=12,
∴,
,
∵BC=15,
∴,
∴=.
例4.如图,已知在中,,垂足为点D,,,
,点E是边的中点.
(1)求边的长;
(2)求的正切值.
(1)解:∵,
∴,
∴,
∵,
∴,
∴;
例4.如图,已知在中,,垂足为点D,,,
,点E是边的中点.
(2)求的正切值.
(2)解:过点E作于点H.
∵,,
∴,
∴,
∵,
∴,
∴,
∴,∴.
如图,在四边形ABCD中,AD∥BC,AB⊥BD于点B.已知∠A = 45°,∠C= 60°,,求AD的长.
解:过点D作DE⊥BC于E
∵ 在Rt△CDE中,∠C = 60°,,
∴,
∵ AB⊥BD,∠A = 45°,∴∠ADB = 45°.
∵AD∥BC,
∴∠DBE =∠ADB = 45°
∴ 在Rt△DBE中,∠DEB = 90°,,
∴ ,
又∵ 在Rt△ABD中,∠ABD= 90°,∠A = 45°,
∴.
1.在中,,,,下列四个选项,正确的是( )
A. B. C. D.
C
2.如图,在中,,,则( )
A. B.2 C. D.
C
3.如图,已知在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足是D,设∠CAB=α,CD=h,那么BC的长度为( )
A. B. C. D.h cosα
B
4.在中,,,,则的度数是( )
A. B. C. D.
D
5.已知:在中,,则BC的值( )
A.只有1个 B.可以有2个 C.可以有3个 D.无数个
B
6.如图,已知第一象限内的点A在反比例函数的图象上,第二象限的点B在反比例函数的图象上,且,则k的值为( )
A. B. C. D.
C
7中,cm,cm,则______.
8.在中,,,是边上的高,,则的长为______.
9.如图,中,,,,则的面积是_______.
10.如图,AD是△ABC的高,,求△ABC的周长.
解:在中,,
∵,,
∴,,
∵在中,,
∴,即,
∴
∴,,
∴△ABC的周长为AB+AC+BD+CD=.
11.如图,在Rt△ABC中,∠C=90°,D是BC边上一点,∠BAD=45°,AC=3,AB=,求BD的长.
解:过D作DE⊥AB于点E,如图所示,
∵∠BAD=45°,
∴∠EAD=∠EDA=45°,
∴AE=DE,
设DE=a,则BE=AB﹣AE=﹣a,
∵AC=3,AB=,∠C=90°,
∴BC=,
∴,
11.如图,在Rt△ABC中,∠C=90°,D是BC边上一点,∠BAD=45°,AC=3,AB=,求BD的长.
∴a=,
经检验,a=是上面方程的解.
∴DE=,BE=2
Rt△BED中,由勾股定理得:
BD2=BE2+DE2=,
∴BD=5.
解直角三角形
1. 了解并掌握解直角三角形的概念;
2. 理解直角三角形中的五个元素之间的联系. (重点)
3. 学会解直角三角形. (难点)
(1)三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
如图,在Rt△ABC中,共有六个元素(三条边,三个角), 其中∠C=90°.
c2
90°
比萨斜塔倾斜程度的问题:
1972年的情形:设塔顶中心点为B,塔身中心线与垂
直中心线的夹角为∠A,过点B向垂直中心线引垂线,垂
足为点C.在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m,
因此
利用计算器可得∠A≈5°28′
类似地,可以求出2001年纠偏后塔身中心线与垂直中心线的夹角.(纠偏后使塔顶中心点偏离垂直中心线的距离比纠偏前减少了43.8cm)
利用计算器可得∠A≈5°51″
比萨斜塔倾斜程度的问题:
1972年的情形:设塔顶中心点为B,塔身中心线与垂
直中心线的夹角为∠A,过点B向垂直中心线引垂线,垂
足为点C.在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m,
因此
利用计算器可得∠A≈5°28′
如果将上述实际问题抽象为数学问题,就是已知直角三角形的斜边和一条直角边,求它的锐角的度数.
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角. 由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
(1)在直角三角形中,除直角外的五个元素之间有哪些关系? (2)知道五个元素中的几个,就可以求其余元素?
(1)三边之间的关系
(2)两锐角之间的关系
(3)边角之间的关系
∠A+∠B=90°
a2+b2=c2(勾股定理)
(3)中的A都可以换成B,同时把a,b互换.
利用这些关系,知道其中的两个元素(至少有一个是边),就可以求出其余三个未知元素.
例1.如图,在Rt△ABC中,∠C=90°,AC=,BC=,解这个直角三角形.
解:∵
∴ ∠A=60°
∠B=90°-∠A=90°-60°=30°
AB=2AC=2
在Rt△ABC中,∠C=90°,a=30,b=20,根据条件解直角三角形.
解:根据勾股定理
例2.如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形(结果保留小数点后一位).
解:
在Rt△ABC中,∠C=90°,∠B=72°,c=14.根据条件解直角三角形.
解:
例3.如图,在△ABC中,sinB=,,AC=5,则△ABC的面积为多少?
D
解:过点A作AD⊥BC,垂足为D.
在RtΔACD中,, AC=5,
∴CD=ACcosC=5=4.
∴由勾股定理得:AD==3.
∵sinB=,
∴∠B=45°.
∴∠BAD=∠B=45°.
∴BD=AD=3.
∴S△ABC=BC AD=(3+4)×3=10.5.
如图,△ABC中,AB=12,BC=15,∠ABC=60°.求tanC的值.
D
解:过点A作AD⊥BC于点D,如图所示:
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵△ABC中,AB=12,
∴,
,
∵BC=15,
∴,
∴=.
例4.如图,已知在中,,垂足为点D,,,
,点E是边的中点.
(1)求边的长;
(2)求的正切值.
(1)解:∵,
∴,
∴,
∵,
∴,
∴;
例4.如图,已知在中,,垂足为点D,,,
,点E是边的中点.
(2)求的正切值.
(2)解:过点E作于点H.
∵,,
∴,
∴,
∵,
∴,
∴,
∴,∴.
如图,在四边形ABCD中,AD∥BC,AB⊥BD于点B.已知∠A = 45°,∠C= 60°,,求AD的长.
解:过点D作DE⊥BC于E
∵ 在Rt△CDE中,∠C = 60°,,
∴,
∵ AB⊥BD,∠A = 45°,∴∠ADB = 45°.
∵AD∥BC,
∴∠DBE =∠ADB = 45°
∴ 在Rt△DBE中,∠DEB = 90°,,
∴ ,
又∵ 在Rt△ABD中,∠ABD= 90°,∠A = 45°,
∴.
1.在中,,,,下列四个选项,正确的是( )
A. B. C. D.
C
2.如图,在中,,,则( )
A. B.2 C. D.
C
3.如图,已知在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足是D,设∠CAB=α,CD=h,那么BC的长度为( )
A. B. C. D.h cosα
B
4.在中,,,,则的度数是( )
A. B. C. D.
D
5.已知:在中,,则BC的值( )
A.只有1个 B.可以有2个 C.可以有3个 D.无数个
B
6.如图,已知第一象限内的点A在反比例函数的图象上,第二象限的点B在反比例函数的图象上,且,则k的值为( )
A. B. C. D.
C
7中,cm,cm,则______.
8.在中,,,是边上的高,,则的长为______.
9.如图,中,,,,则的面积是_______.
10.如图,AD是△ABC的高,,求△ABC的周长.
解:在中,,
∵,,
∴,,
∵在中,,
∴,即,
∴
∴,,
∴△ABC的周长为AB+AC+BD+CD=.
11.如图,在Rt△ABC中,∠C=90°,D是BC边上一点,∠BAD=45°,AC=3,AB=,求BD的长.
解:过D作DE⊥AB于点E,如图所示,
∵∠BAD=45°,
∴∠EAD=∠EDA=45°,
∴AE=DE,
设DE=a,则BE=AB﹣AE=﹣a,
∵AC=3,AB=,∠C=90°,
∴BC=,
∴,
11.如图,在Rt△ABC中,∠C=90°,D是BC边上一点,∠BAD=45°,AC=3,AB=,求BD的长.
∴a=,
经检验,a=是上面方程的解.
∴DE=,BE=2
Rt△BED中,由勾股定理得:
BD2=BE2+DE2=,
∴BD=5.
