第24章 圆 小结与复习 课件(共35张PPT)
文档属性
| 名称 | 第24章 圆 小结与复习 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 634.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 13:18:34 | ||
图片预览







文档简介
(共35张PPT)
小结与复习
第24章 圆 小结与复习
要点梳理
一.旋转的有关概念及性质
1.在平面内,一个图形绕着一个定点(如点O),旋转一定的角度(如θ),得到另一个图形的变换,叫做_____.定点O叫做__________,θ叫做_______.
旋转
旋转中心
旋转角
(1) 对应点到旋转中心的距离相等;
(2) 两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
(3)旋转中心是唯一不动的点.
3.旋转的性质
2.在平面内,一个图形绕着一个定点旋转一定的角度
后,能够与原图形重合,这样的图形叫做______________,这个定点就是__________ .
旋转对称图形
旋转中心
第24章 圆 小结与复习
1.把一个图形(如△ABO)绕定点O旋转180 ,得到一个能够与它重合的图形(如△CDO),这时,图形△ABO与图形△CDO关于点O的对称叫做_________,点O就是________.这两个图形中的对应点叫做关于中心的_________.
二.中心对称的有关概念及性质
中心对称
对称中心
对称点
2.把一个图形绕某一个定点旋转180°,如果旋转后的图形能和原来图形重合,那么这个图形叫做_______________,这个定点叫做它的_________,互相重合的点叫做________.
中心对称图形
对称中心
对称点
成中心对称的两个图形中,对称点的连线经过_________,且被对称中心________.
3.中心对称的性质
对称中心
平分
第24章 圆 小结与复习
三、圆的基本概念及性质
1.定义:到定点的距离等于定长的点的集合叫做圆.
2.有关概念:
(1)弦、直径(圆中最长的弦)
(2)弧、优弧、劣弧、等弧
(3)弦心距
.
O
第24章 圆 小结与复习
四、点与圆的位置关系
●A
●B
●C
点与圆的位置关系 点到圆心的距离d与圆的半径r之间关系
点在圆外
点在圆上
点在圆内
●O
d
r
d﹥r
d=r
d﹤r
第24章 圆 小结与复习
五、圆的对称性
1.圆是轴对称图形,经过圆心的每一条直线都是
它的对称轴.圆有无数条对称轴.
2.圆是中心对称图形,并且绕圆心旋转任何一
个角度都能与自身重合,即圆具有旋转不变性.
.
第24章 圆 小结与复习
3.在同圆或等圆中,相等的圆心角所对的弧相等,
所对的弦也相等.
4.在同圆或等圆中,如果两个圆心角、两条弧、
两条弦中有一组量相等,那么它们所对应的其余
各组量都分别相等.
第24章 圆 小结与复习
●O
A
B
C
D
M└
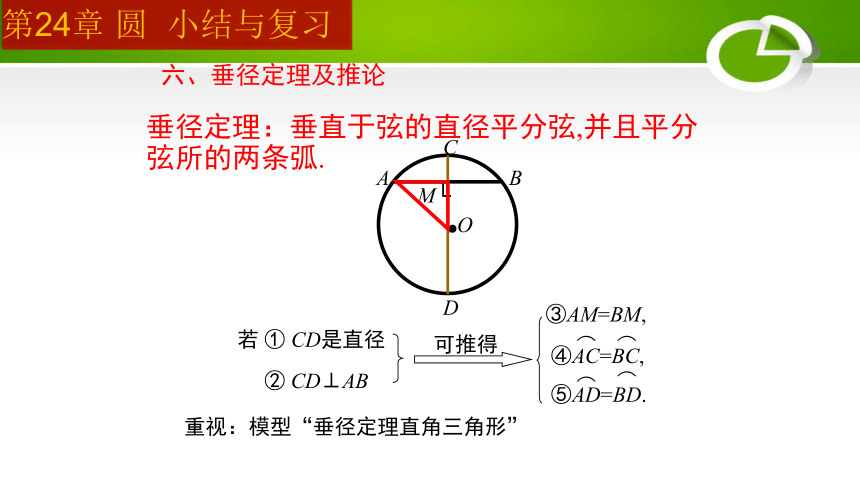
③AM=BM,
重视:模型“垂径定理直角三角形”
若 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
垂径定理:垂直于弦的直径平分弦,并且平分弦所的两条弧.
六、垂径定理及推论
第24章 圆 小结与复习
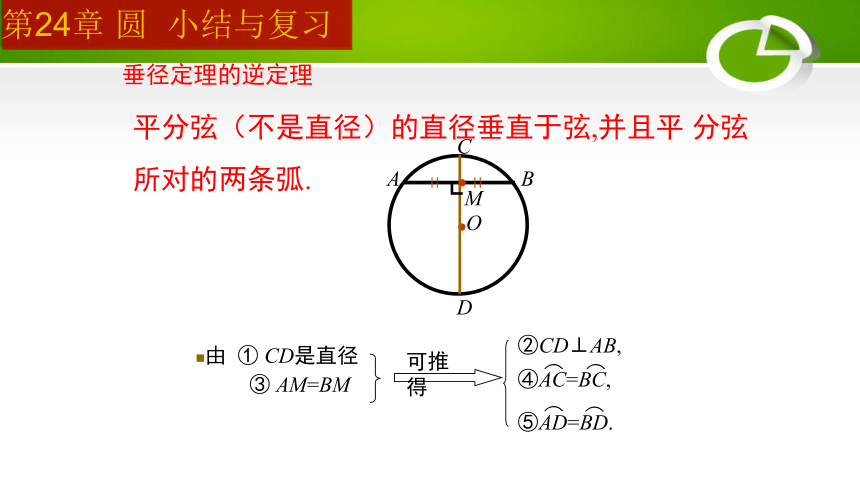
垂径定理的逆定理
②CD⊥AB,
由 ① CD是直径
③ AM=BM
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
●O
C
D
A
B
●
┗
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
M
第24章 圆 小结与复习
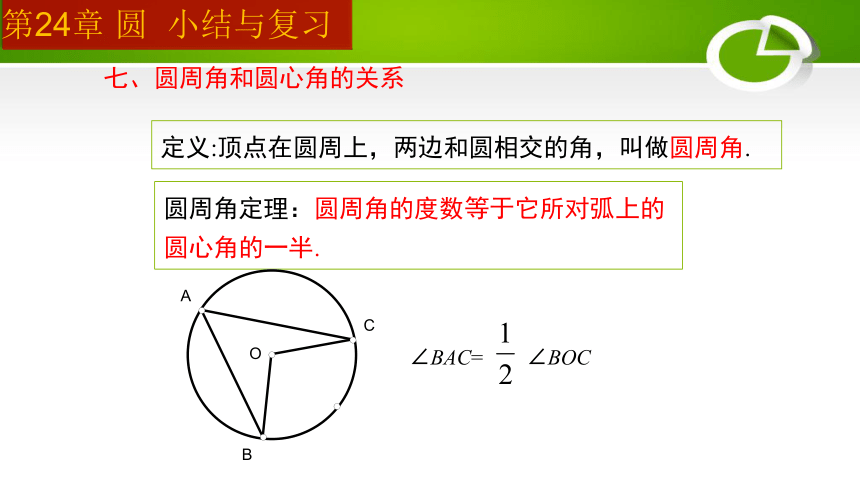
定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.
圆周角定理:圆周角的度数等于它所对弧上的圆心角的一半.
七、圆周角和圆心角的关系
∠BAC= ∠BOC
第24章 圆 小结与复习
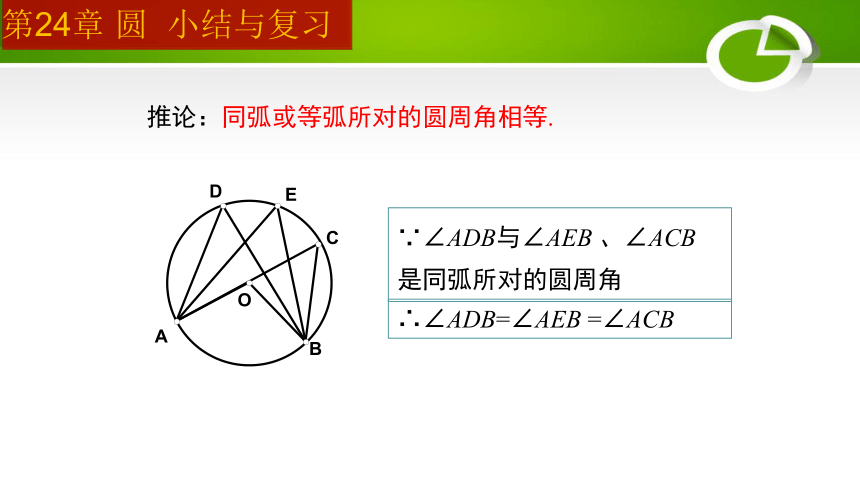
推论:同弧或等弧所对的圆周角相等.
∵∠ADB与∠AEB 、∠ACB 是同弧所对的圆周角
∴∠ADB=∠AEB =∠ACB
第24章 圆 小结与复习
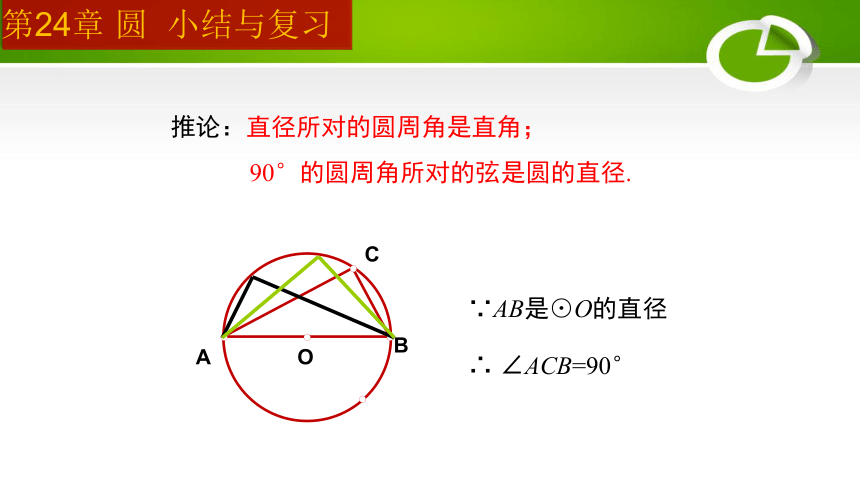
推论:直径所对的圆周角是直角;
90°的圆周角所对的弦是圆的直径.
∵AB是⊙O的直径
∴ ∠ACB=90°
第24章 圆 小结与复习
八、直线和圆的位置关系
直线与圆的位置关系 圆心与直线的距离d与圆的半径r的关系 直线名称 直线与圆的交点个数
相离
相切
相交
●
l
d
r
0
切线
d﹤r
割线
2
d﹥r
—
d=r
1
第24章 圆 小结与复习
九、切线的判定与性质
1.切线的判定一般有三种方法:
a.定义法:和圆有唯一的一个公共点
b.距离法: d=r
c.判定定理:过半径的外端点且垂直于半径的直线
是圆的切线.
2.切线的性质:
圆的切线垂直于经过且点的半径.
第24章 圆 小结与复习
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
切线长:
从圆外一点引圆的切线,这个点与切点间的线段的长称为切线长.
3.切线长及切线长定理
第24章 圆 小结与复习
十、三角形的内切圆及内心
1.与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做三角形的内心.
3.这个三角形叫做圆的外切三角形.
4.三角形的内心就是三角形的三个内角角平分线的交点.
┐
A
C
I
┐
┐
D
E
F
三角形的内心到三角形的三边的距离相等.
重要结论
B
第24章 圆 小结与复习
十一、圆内接正多边形
O
C
D
A
B
M
半径R
圆心角
弦心距r
弦a
圆心
中心角
A
B
C
D
E
F
O
半径R
边心距r
中心
类比学习
圆内接正多边形
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
边心距
正多边形的边心距
1.概念
第24章 圆 小结与复习
①正多边形的内角和=
②中心角=
圆内接正多边形的有
关概念及性质
2.计算公式
第24章 圆 小结与复习
十二、 圆中的计算问题
1.弧长公式
半径为R的圆中,n°圆心角所对的弧长l=________.
2.扇形面积公式
半径为R,圆心角为n°的扇形面积S= ____________.
或
3.弓形面积公式
O
O
弓形的面积=扇形的面积±三角形的面积
第24章 圆 小结与复习
(3)圆锥的侧面积为 .
[注意] 圆锥的侧面展开图的形状是扇形,它的半径等于圆锥的母线长,它的弧长是圆锥底面圆的周长.
4.圆锥的侧面积
(1)圆锥的侧面展开图是一个 .
(2)如果圆锥母线长为l,底面圆的半径为r,那么这个扇形的半径为 ,扇形的弧长为 .
扇形
l
第24章 圆 小结与复习
考点一 旋转变换
1. 如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
解析:(1)根据题意,找准旋转中心,旋转方向及旋转角度,补全图形即可;
(2)由旋转的性质得∠DCF为直角,由EF与CD平行,得到∠EFC为直角,利用SAS得到△BDC与△EFC全等,利用全等三角形对应角相等即可得证.
考点精讲
第24章 圆 小结与复习
F
解:(1)补全图形,如图所示;
(2)由旋转的性质得,DC=FC,∠DCF=90°,
∴∠DCE+∠ECF=90°.
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD,
∵EF∥DC,∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
第24章 圆 小结与复习
考点二 与圆有关的概念
2. 在图中,BC是⊙O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是( )
A. 72° B.54° C. 45° D.36 °
A
B
C
D
解析 根据圆周角定理的推论可知, ∠B= ∠D=36°, ∠BAC=90°,所以∠BAD=54°,故选B.
B
O
第24章 圆 小结与复习
3 如图,工程上常用钢珠来测量零件上小圆孔的口宽,假设钢珠的直径是 10 mm,测得钢珠顶端离零件表面的距离为 8 mm,则这个小圆孔的口宽 AB = mm.
8 mm
A
B
解析 连接 OA,过点 O 作出弓形的高 CD,则 AO = 5 mm,OD = 3 mm,利用勾股定理可算得 AD = 4 mm,所以 AB = 8 mm.
方法归纳 在圆中涉及弓形求线段长问题时,常构造直角三角形来解决.
8
C
D
O
考点三 垂径定理及其应用
第24章 圆 小结与复习
4. 如图,⊙O的直径AE=4cm,∠B=30 °,则AC= .
A
B
C
E
O
2cm
解析 连接CE,则∠E= ∠B=30°, ∠ACE=90°,所以AC= AE=2cm.
方法归纳:有直径,通常构造直径所对的圆周角,将问题转化到直角三角形中解决.
考点四 圆周角定理
第24章 圆 小结与复习
考点五 点或直线与圆的位置关系
5. 如图,已知∠NON=30°,P是ON上的一点,OP=5㎝,若以P点为圆心,r为半径画圆,使射线OM与⊙P只有一个公共点,求r的值或取值范围.
解:当射线OM与⊙P相切时,射线OM
与⊙P只有一个公共点.
过点P作PA⊥OM于A,如图所示.
在Rt△AOP中,r=PA=OP·sin∠POA=2.5(㎝).
第24章 圆 小结与复习
当射线OM与⊙P相交且点O在⊙P内时,射线OM与⊙P只有一个公共点.如图2所示.
∵射线OM与⊙P相交,则r>2.5㎝ ···①
又∵点O在⊙P内,则r>OP,即r>5㎝ ···②
综合①、②可得r>5.
综上所述,当射线OM与⊙P
只有一个公共点时,r=2.5㎝或r>5㎝.
图2
第24章 圆 小结与复习
6. 如图,以△ABC的边AB为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.问:BC与⊙O是否相切?
解:BC与⊙O相切.理由:连接OD,BD,如图.∵DE切⊙O于D,AB为直径,
∴∠EDO=∠ADB=90°.
又∵DE平分CB,∴DE= BC=BE.
∴∠EDB=∠EBD.
又∵∠ODB=∠OBD,∠ODB+∠EDB=90°,∴∠OBD+∠DBE=90°,
即∠ABC=90°.∴BC与⊙O相切.
考点六 切线的性质与判定
第24章 圆 小结与复习
如图,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,
求图中阴影部分的面积.
【解析】观察图形看出,因为四边形ABCD是正方形,所以AC是圆的直径.由于AE,CF都与EF垂直,所以AE与CF平行,所以可以把CF平移到直线AE上,如果点E,F重合时,点C到达点C'的位置,则构造出一个直角三角形AC'C,在这个直角三角形中利用勾股定理,即可求得正方形ABCD的外接圆的半径,进而求得阴影部分的面积.
考点七 圆内接正多边形
第24章 圆 小结与复习
解:将线段FC平移到直线AE上,此时点F与点E重合,
点C到达点C'的位置.连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在Rt△AC'C中,得
∴正方形ABCD外接圆的半径为 .
∴正方形ABCD的边长为
第24章 圆 小结与复习
8.(1)一条弧所对的圆心角为135 ° ,弧长等于半径为5cm的圆的周长的3倍,则这条弧的半径为 .
(2)一个底面直径为10cm,母线长为15cm的圆锥,它的侧面展开图圆心角是 度.
40cm
120
解析 (1)要熟记弧长公式及其变形式公式.即
及 ;还要熟记圆锥及其侧面展开图之间存在的对应的数量关系,即底面圆的周长等于展开后扇形的弧长,母线长等展开后扇形的半径.
考点八 弧长和扇形面积
第24章 圆 小结与复习
10. 如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A,B两点,连接AP并延长分别交⊙P,x轴于点D,E,连接DC并延长交y轴于点F,若点F的坐标为(0,1),点D的坐标为(6,﹣1).
(1)求证:CD=CF;
(2)判断⊙P与x轴的位置关系,并说明理由;
(3)求直线AD的函数表达式.
考点九 有关圆的综合性题目
第24章 圆 小结与复习
(1)证明:过点D作DH⊥x轴于H,则∠CHD=∠COF=90°,如图所示.
∵点F(0,1),点D(6,-1),∴DH=OF=1.
∵∠FCO=∠DCH,
∴△FOC≌△DHC,
∴CD=CF.
(2)解:⊙P与x轴相切.理由如下:
连接CP,如图所示.
∵AP=PD,CD=CF,∴CP∥AF.
∴∠PCE=∠AOC=90°.
∴⊙P与x轴相切.
第24章 圆 小结与复习
(3)由(2)可知CP是△ADF的中位线.
∴AF=2CP. ∵AD=2CP,∴AD=AF.
连接BD,如图所示.∵AD为⊙P的直径,
∴∠ABD=90°.
∴BD=OH=6,OB=DH=OF=1.
设AD=x,则AB=AF-BF=AD-BF=AD-(OB+OF)= x-2.
在Rt△ABD中,由勾股定理,得
AD2=AB2+BD2,即x2=(x-2)2+62,解得 x=10.
∴OA=AB+OB=8+1=9. ∴点A(0,-9).
设直线AD的函数表达式为y=kx+b,
把点A(0,-9),D(6,-1)代入,得
解得
∴直线AD的函数表达式为 .
第24章 圆 小结与复习
课堂小结
圆
旋转
旋转对称及其性质
中心对称及其性质
旋转对称图形
中心对称图形
圆的基本性质
垂径分弦
等圆心角
圆的确定
连半径,作弦心距,构造直角三角形
等弧
等弦
等弦心距
三角形的外接圆
圆周角
圆内接四边形的性质
作弦,构造直径所对的圆周角
与圆有关的位置关系
点与圆的位置关系
直线与圆的位置的关系
有公共点,连半径,证垂直;无公共点,作垂直,证半径;见切点,连半径,得垂直.
与圆有关的计算
正多边形的计算
弧长与扇形面积的计算
切线的判定与性质
第24章 圆 小结与复习
小结与复习
第24章 圆 小结与复习
要点梳理
一.旋转的有关概念及性质
1.在平面内,一个图形绕着一个定点(如点O),旋转一定的角度(如θ),得到另一个图形的变换,叫做_____.定点O叫做__________,θ叫做_______.
旋转
旋转中心
旋转角
(1) 对应点到旋转中心的距离相等;
(2) 两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
(3)旋转中心是唯一不动的点.
3.旋转的性质
2.在平面内,一个图形绕着一个定点旋转一定的角度
后,能够与原图形重合,这样的图形叫做______________,这个定点就是__________ .
旋转对称图形
旋转中心
第24章 圆 小结与复习
1.把一个图形(如△ABO)绕定点O旋转180 ,得到一个能够与它重合的图形(如△CDO),这时,图形△ABO与图形△CDO关于点O的对称叫做_________,点O就是________.这两个图形中的对应点叫做关于中心的_________.
二.中心对称的有关概念及性质
中心对称
对称中心
对称点
2.把一个图形绕某一个定点旋转180°,如果旋转后的图形能和原来图形重合,那么这个图形叫做_______________,这个定点叫做它的_________,互相重合的点叫做________.
中心对称图形
对称中心
对称点
成中心对称的两个图形中,对称点的连线经过_________,且被对称中心________.
3.中心对称的性质
对称中心
平分
第24章 圆 小结与复习
三、圆的基本概念及性质
1.定义:到定点的距离等于定长的点的集合叫做圆.
2.有关概念:
(1)弦、直径(圆中最长的弦)
(2)弧、优弧、劣弧、等弧
(3)弦心距
.
O
第24章 圆 小结与复习
四、点与圆的位置关系
●A
●B
●C
点与圆的位置关系 点到圆心的距离d与圆的半径r之间关系
点在圆外
点在圆上
点在圆内
●O
d
r
d﹥r
d=r
d﹤r
第24章 圆 小结与复习
五、圆的对称性
1.圆是轴对称图形,经过圆心的每一条直线都是
它的对称轴.圆有无数条对称轴.
2.圆是中心对称图形,并且绕圆心旋转任何一
个角度都能与自身重合,即圆具有旋转不变性.
.
第24章 圆 小结与复习
3.在同圆或等圆中,相等的圆心角所对的弧相等,
所对的弦也相等.
4.在同圆或等圆中,如果两个圆心角、两条弧、
两条弦中有一组量相等,那么它们所对应的其余
各组量都分别相等.
第24章 圆 小结与复习
●O
A
B
C
D
M└
③AM=BM,
重视:模型“垂径定理直角三角形”
若 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
垂径定理:垂直于弦的直径平分弦,并且平分弦所的两条弧.
六、垂径定理及推论
第24章 圆 小结与复习
垂径定理的逆定理
②CD⊥AB,
由 ① CD是直径
③ AM=BM
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
●O
C
D
A
B
●
┗
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
M
第24章 圆 小结与复习
定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.
圆周角定理:圆周角的度数等于它所对弧上的圆心角的一半.
七、圆周角和圆心角的关系
∠BAC= ∠BOC
第24章 圆 小结与复习
推论:同弧或等弧所对的圆周角相等.
∵∠ADB与∠AEB 、∠ACB 是同弧所对的圆周角
∴∠ADB=∠AEB =∠ACB
第24章 圆 小结与复习
推论:直径所对的圆周角是直角;
90°的圆周角所对的弦是圆的直径.
∵AB是⊙O的直径
∴ ∠ACB=90°
第24章 圆 小结与复习
八、直线和圆的位置关系
直线与圆的位置关系 圆心与直线的距离d与圆的半径r的关系 直线名称 直线与圆的交点个数
相离
相切
相交
●
l
d
r
0
切线
d﹤r
割线
2
d﹥r
—
d=r
1
第24章 圆 小结与复习
九、切线的判定与性质
1.切线的判定一般有三种方法:
a.定义法:和圆有唯一的一个公共点
b.距离法: d=r
c.判定定理:过半径的外端点且垂直于半径的直线
是圆的切线.
2.切线的性质:
圆的切线垂直于经过且点的半径.
第24章 圆 小结与复习
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
切线长:
从圆外一点引圆的切线,这个点与切点间的线段的长称为切线长.
3.切线长及切线长定理
第24章 圆 小结与复习
十、三角形的内切圆及内心
1.与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做三角形的内心.
3.这个三角形叫做圆的外切三角形.
4.三角形的内心就是三角形的三个内角角平分线的交点.
┐
A
C
I
┐
┐
D
E
F
三角形的内心到三角形的三边的距离相等.
重要结论
B
第24章 圆 小结与复习
十一、圆内接正多边形
O
C
D
A
B
M
半径R
圆心角
弦心距r
弦a
圆心
中心角
A
B
C
D
E
F
O
半径R
边心距r
中心
类比学习
圆内接正多边形
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
边心距
正多边形的边心距
1.概念
第24章 圆 小结与复习
①正多边形的内角和=
②中心角=
圆内接正多边形的有
关概念及性质
2.计算公式
第24章 圆 小结与复习
十二、 圆中的计算问题
1.弧长公式
半径为R的圆中,n°圆心角所对的弧长l=________.
2.扇形面积公式
半径为R,圆心角为n°的扇形面积S= ____________.
或
3.弓形面积公式
O
O
弓形的面积=扇形的面积±三角形的面积
第24章 圆 小结与复习
(3)圆锥的侧面积为 .
[注意] 圆锥的侧面展开图的形状是扇形,它的半径等于圆锥的母线长,它的弧长是圆锥底面圆的周长.
4.圆锥的侧面积
(1)圆锥的侧面展开图是一个 .
(2)如果圆锥母线长为l,底面圆的半径为r,那么这个扇形的半径为 ,扇形的弧长为 .
扇形
l
第24章 圆 小结与复习
考点一 旋转变换
1. 如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
解析:(1)根据题意,找准旋转中心,旋转方向及旋转角度,补全图形即可;
(2)由旋转的性质得∠DCF为直角,由EF与CD平行,得到∠EFC为直角,利用SAS得到△BDC与△EFC全等,利用全等三角形对应角相等即可得证.
考点精讲
第24章 圆 小结与复习
F
解:(1)补全图形,如图所示;
(2)由旋转的性质得,DC=FC,∠DCF=90°,
∴∠DCE+∠ECF=90°.
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD,
∵EF∥DC,∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
第24章 圆 小结与复习
考点二 与圆有关的概念
2. 在图中,BC是⊙O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是( )
A. 72° B.54° C. 45° D.36 °
A
B
C
D
解析 根据圆周角定理的推论可知, ∠B= ∠D=36°, ∠BAC=90°,所以∠BAD=54°,故选B.
B
O
第24章 圆 小结与复习
3 如图,工程上常用钢珠来测量零件上小圆孔的口宽,假设钢珠的直径是 10 mm,测得钢珠顶端离零件表面的距离为 8 mm,则这个小圆孔的口宽 AB = mm.
8 mm
A
B
解析 连接 OA,过点 O 作出弓形的高 CD,则 AO = 5 mm,OD = 3 mm,利用勾股定理可算得 AD = 4 mm,所以 AB = 8 mm.
方法归纳 在圆中涉及弓形求线段长问题时,常构造直角三角形来解决.
8
C
D
O
考点三 垂径定理及其应用
第24章 圆 小结与复习
4. 如图,⊙O的直径AE=4cm,∠B=30 °,则AC= .
A
B
C
E
O
2cm
解析 连接CE,则∠E= ∠B=30°, ∠ACE=90°,所以AC= AE=2cm.
方法归纳:有直径,通常构造直径所对的圆周角,将问题转化到直角三角形中解决.
考点四 圆周角定理
第24章 圆 小结与复习
考点五 点或直线与圆的位置关系
5. 如图,已知∠NON=30°,P是ON上的一点,OP=5㎝,若以P点为圆心,r为半径画圆,使射线OM与⊙P只有一个公共点,求r的值或取值范围.
解:当射线OM与⊙P相切时,射线OM
与⊙P只有一个公共点.
过点P作PA⊥OM于A,如图所示.
在Rt△AOP中,r=PA=OP·sin∠POA=2.5(㎝).
第24章 圆 小结与复习
当射线OM与⊙P相交且点O在⊙P内时,射线OM与⊙P只有一个公共点.如图2所示.
∵射线OM与⊙P相交,则r>2.5㎝ ···①
又∵点O在⊙P内,则r>OP,即r>5㎝ ···②
综合①、②可得r>5.
综上所述,当射线OM与⊙P
只有一个公共点时,r=2.5㎝或r>5㎝.
图2
第24章 圆 小结与复习
6. 如图,以△ABC的边AB为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.问:BC与⊙O是否相切?
解:BC与⊙O相切.理由:连接OD,BD,如图.∵DE切⊙O于D,AB为直径,
∴∠EDO=∠ADB=90°.
又∵DE平分CB,∴DE= BC=BE.
∴∠EDB=∠EBD.
又∵∠ODB=∠OBD,∠ODB+∠EDB=90°,∴∠OBD+∠DBE=90°,
即∠ABC=90°.∴BC与⊙O相切.
考点六 切线的性质与判定
第24章 圆 小结与复习
如图,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,
求图中阴影部分的面积.
【解析】观察图形看出,因为四边形ABCD是正方形,所以AC是圆的直径.由于AE,CF都与EF垂直,所以AE与CF平行,所以可以把CF平移到直线AE上,如果点E,F重合时,点C到达点C'的位置,则构造出一个直角三角形AC'C,在这个直角三角形中利用勾股定理,即可求得正方形ABCD的外接圆的半径,进而求得阴影部分的面积.
考点七 圆内接正多边形
第24章 圆 小结与复习
解:将线段FC平移到直线AE上,此时点F与点E重合,
点C到达点C'的位置.连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在Rt△AC'C中,得
∴正方形ABCD外接圆的半径为 .
∴正方形ABCD的边长为
第24章 圆 小结与复习
8.(1)一条弧所对的圆心角为135 ° ,弧长等于半径为5cm的圆的周长的3倍,则这条弧的半径为 .
(2)一个底面直径为10cm,母线长为15cm的圆锥,它的侧面展开图圆心角是 度.
40cm
120
解析 (1)要熟记弧长公式及其变形式公式.即
及 ;还要熟记圆锥及其侧面展开图之间存在的对应的数量关系,即底面圆的周长等于展开后扇形的弧长,母线长等展开后扇形的半径.
考点八 弧长和扇形面积
第24章 圆 小结与复习
10. 如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A,B两点,连接AP并延长分别交⊙P,x轴于点D,E,连接DC并延长交y轴于点F,若点F的坐标为(0,1),点D的坐标为(6,﹣1).
(1)求证:CD=CF;
(2)判断⊙P与x轴的位置关系,并说明理由;
(3)求直线AD的函数表达式.
考点九 有关圆的综合性题目
第24章 圆 小结与复习
(1)证明:过点D作DH⊥x轴于H,则∠CHD=∠COF=90°,如图所示.
∵点F(0,1),点D(6,-1),∴DH=OF=1.
∵∠FCO=∠DCH,
∴△FOC≌△DHC,
∴CD=CF.
(2)解:⊙P与x轴相切.理由如下:
连接CP,如图所示.
∵AP=PD,CD=CF,∴CP∥AF.
∴∠PCE=∠AOC=90°.
∴⊙P与x轴相切.
第24章 圆 小结与复习
(3)由(2)可知CP是△ADF的中位线.
∴AF=2CP. ∵AD=2CP,∴AD=AF.
连接BD,如图所示.∵AD为⊙P的直径,
∴∠ABD=90°.
∴BD=OH=6,OB=DH=OF=1.
设AD=x,则AB=AF-BF=AD-BF=AD-(OB+OF)= x-2.
在Rt△ABD中,由勾股定理,得
AD2=AB2+BD2,即x2=(x-2)2+62,解得 x=10.
∴OA=AB+OB=8+1=9. ∴点A(0,-9).
设直线AD的函数表达式为y=kx+b,
把点A(0,-9),D(6,-1)代入,得
解得
∴直线AD的函数表达式为 .
第24章 圆 小结与复习
课堂小结
圆
旋转
旋转对称及其性质
中心对称及其性质
旋转对称图形
中心对称图形
圆的基本性质
垂径分弦
等圆心角
圆的确定
连半径,作弦心距,构造直角三角形
等弧
等弦
等弦心距
三角形的外接圆
圆周角
圆内接四边形的性质
作弦,构造直径所对的圆周角
与圆有关的位置关系
点与圆的位置关系
直线与圆的位置的关系
有公共点,连半径,证垂直;无公共点,作垂直,证半径;见切点,连半径,得垂直.
与圆有关的计算
正多边形的计算
弧长与扇形面积的计算
切线的判定与性质
第24章 圆 小结与复习
