专题2.4 二次函数的应用(第2课时) 课件(共29张PPT)
文档属性
| 名称 | 专题2.4 二次函数的应用(第2课时) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
第二章 二次函数
2.4 二次函数的应用
第2课时 利润最大问题
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、熟练掌握用二次函数的性质求出商品利润的最大值问题,学会根据具体情况,由二次函数的性质,表示出正确的最大值;
2、学会根据实际问题的自变量的取值范围求出符合条件的商品利润具体值,可以准确掌握二次函数的实际应用;
导入新课
观察与思考
赶集,是中国一直以来就有的传统,尤其是过年期间,更是热闹!
思考:商品买卖过程中,作为商家利润最大化是永恒的追求.如果你是商家,如何定价才能获得最大利润呢?
讲授新课
知识点一 根据题意表示出利润问题中的数量关系
某商品现在的售价为每件100元,每星期可卖出300件,已知商品的进价为每件60元,则每星期销售额是 元,销售利润 元.
探究交流
30000
12000
数量关系
(1)销售额= 售价×销售量;
(2)利润= 销售额-总成本=单件利润×销售量;
(3)单件利润=售价-进价.
知识点二 利润最大问题解决思路
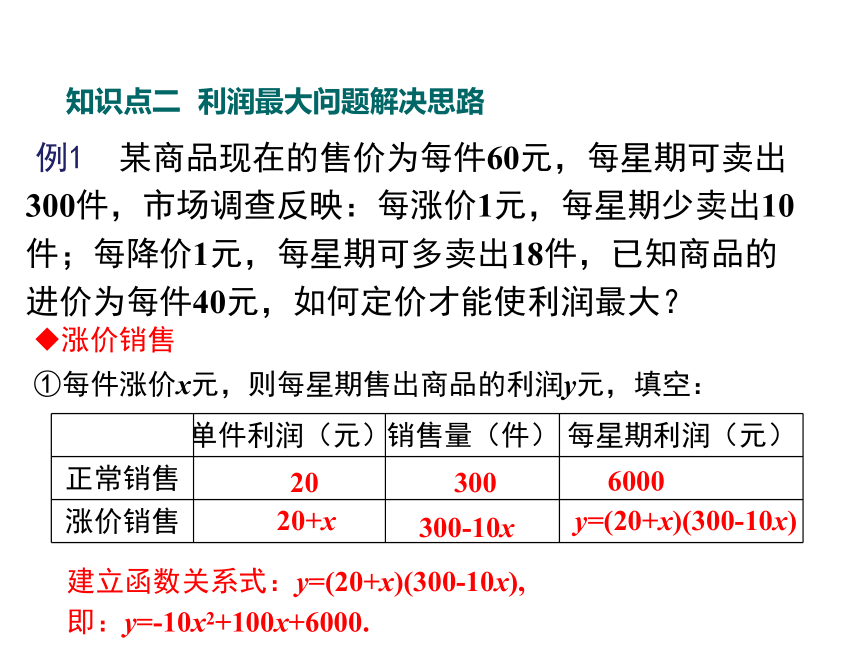
例1 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
涨价销售
①每件涨价x元,则每星期售出商品的利润y元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
涨价销售
20
300
20+x
300-10x
y=(20+x)(300-10x)
建立函数关系式:y=(20+x)(300-10x),
即:y=-10x2+100x+6000.
6000
②自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
当 时,y=-10×52+100×5+6000=6250.
即涨价5元时,最大利润是6250元.
降价销售
①每件降价x元,则每星期售出商品的利润y元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
降价销售
20
300
20-x
300+18x
y=(20-x)(300+18x)
建立函数关系式:y=(20-x)(300+18x),
即:y=-18x2+60x+6000.
例2 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
6000
综合可知,应定价58元时,才能使利润最大。
②自变量x的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤20.
③降价多少元时,利润最大,是多少?
当 时,
即降价 元时,最大利润是6050元.
即:y=-18x2+60x+6000,
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗
知识要点
求解最大利润问题的一般步骤
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润
×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
y=(160+10x)(120-6x)
例3 某旅馆有客房120间,每间房的日租金为160元,每天都客满.经市场调查,如果一间客房日租金每增加10元,则客房每天少出租6间,不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高?最高总收入是多少?
解:设每间客房的日租金提高10x元,则每天客房出租数会
减少6x间,设客房日租金为y万元,则
当x=2时,y有最大值,且y最大=19440.
答:每间客房的日租金提高到180元时,客房日租金的总收入
最高,最大收入为19440.
=-60(x-2)2+19440.
∵x≥0,且120-6x>0,
∴0≤x<20.
这时每间客房的日租金为160+10×2=180(元).
当堂练习
1.将进货单价为30元的某种商品按零售价100元1件卖出时,每天能卖出20件.若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1件,为了获得最大的利润,则应降价( )
A.5元 B.15元 C.25元 D.35元
【答案】C
【详解】解:设应降价x元,根据题意得,
y=(100-x-30)(20+x)=-x2+50x+1400=-(x-25)2+2025.
∵-1<0,
∴ 当x=25时,y取得最大值,
为了获得最大的利润,则应降价25元.
故选C.
2.某景区旅店有30张床位,每床每天收费10元时,可全部租出,若每床每天收费提高10元,则有2张床位不能租出;若每床每天收费再提高10元,则再有2张床位不能租出;若每次按提高10元的这种方法变化下去,则该旅店每天营业收入最多为( )
A.3125元 B.3120元 C.2950元 D.1280元
【答案】D
【详解】解:设每床每晚收费提高x个10元,旅店每天营业收入为y元,
根据题意得:
y=(10+10x)(30-2x)
=-20x2+280x+300
=-20(x-7)2+1280
∴当x=7时,y最大,最大值为1280元,
∴该旅店每天营业收入最多为1280元,
故选:D.
3.某服装店购进单价为15元的童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,为使该服装店平均每天的销售利润最大,则每件的定价为( )
A.21元 B.22元 C.23元 D.24元
【答案】B
【详解】解:设每天的销售利润为w元,每件的定价为x元,则每件的利润为(x-15)元,平均每天售出8+件, 根据题意得:
y=(x-15)(-2x+58)=-2x2+88x-870=-2(x-22)2+98,
∵ -2<0
∴当x=22时, w最大,
即每件的定价为22元时,每天的销售利润最大.
故选:B
4.某超市销售一种商品,每件成本为50元,销售人员经调查发现,该商品每月的销售量y(件)与销售单价x(元)之间满足函数关系式y=-5x+550,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.90元,4500元 B.80元,4500元
C.90元,4000元 D.80元,4000元
【答案】B
【详解】解:设每月总利润为w,
依题意得:w=y(x-50)
=(-5x+550)(x-50)
=-5x2+800x-27500
=-5(x-80)2+4500
∵-5<0,此图象开口向下,又x≥50,
∴当x=80时,w有最大值,最大值为4500元.
故选:B.
5.某件商品的销售利润y(元)与商品单价x(元)之间满足y=-x2+6x-7,不考虑其他因素,该商品的单价定为__________元时,销售一件该商品获得的利润最大,最大利润为__________元.
【答案】 3 2
【详解】解:∵某件商品的销售利润y(元)与商品单价x(元)之间满足
y=-x2+6x-7=-(x-3)2+2,a=-1<0,
∴该商品的单价定为3元时,销售一件该商品获得的利润最大,最大利润为2元,
故答案为:3;2.
6.某服装店销售一批服装,平均每天可售出20件,每件盈利40元,为了扩大销售,尽快减少库存,商店决定采取适当的降价措施,经市场调查发现,如果一件衣服每降价1元,商店平均每天可多售出2件,则每件衣服降价___________元时,服装店每天盈利最多.
【答案】15
【详解】解:设每件衣服降价x元,获得的总利润为y元,
由题意得:y=(40-x)(20+2x),
整理得:y=-2x2+60x+800=-2(x-15)2+1250,
∴当x=15时,y取得最大值;
故答案为:15.
7.某果园有100棵苹果树,平均每棵树可结660个苹果,根据经验估计,在这个果园里每多种一棵树,平均每棵树就会少结6个苹果,则果园里增____棵苹果树,所结苹果的总数最多.
【答案】5
【详解】解:设果园里增x棵苹果树,所结苹果的总数为y,
根据题意得y=(100+x)(660﹣6x)
=﹣6x2+60x+66000
=﹣6(x﹣5)2+66150,
∵a=﹣6,
∴当x=5时,y有最大值66150,
即果园里增5棵苹果树,所结苹果的总数最多.
故答案为5.
8.某企业研发出了一种新产品准备销售,已知研发、生产这种产品的成本为30元/件,据调查年销售量y(万件)关于售价x(元/件)的函数解析式为: ,则当该产品的售价x为________.(元/件)时,企业销售该产品获得的年利润最大.
【答案】50
【详解】解:设企业销售该产品获得的年利润为w元,根据题意得:
当40≤x<60时,
w=(x-30)(-2x+140)=-2x2+200x-4200=-2(x-50)2+800,
∵-2<0,
∴当x=50时,w有最大值,最大值为800;
当60≤x≤70时,
w=(x-30)(-x+80)=-x2+110x-2400=-(x-55)2+625,
∵-1<0,
∴当x>55时,w随x的增大而减小,
∴当x=60时,w有最大值,最大值为600;
∵800>600,
∴当x=50时,w有最大值,
即当该产品的售价x为50(元/件)时,企业销售该产品获得的年利润最大.
故答案为:50
9.超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间满足一次函数关系(其中10<x<25,且x为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.
(1)求y与x之间的函数关系式;
(2)设超市销售该品牌洗手液每天销售利润为w元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
【答案】(1)y=-5x+150(10<x<25)
(2)当每瓶洗手液的售价定为20元时,利润最大,最大利润是500元.
【详解】(1)解:设y=kx+b,
由题意得:,解得:,
∴y=-5x+150(10<x<25);
(2)解:由题意得:
w=(x-10)(-5x+150)
=-5x2+200x-1500
=-5(x-20)2+500
∵a=-5<0,抛物线开口朝下,w有最大值,
∵10<x<25,
∴当x=20时,w有最大值:500;
∴当每瓶洗手液的售价定为20元时,利润最大,最大利润是500元.
10.端午节前夕,某超市从厂家分两次购进A、B两种品牌的粽子,两次进货时,两种品牌粽子的进价不变.第一次购进A品牌粽子100袋和B品牌粽子150袋,总费用为7000元;第二次购进A品牌粽子180袋和B品牌粽子120袋,总费用为8100元.
(1)求A、B两种品牌粽子每袋的进价各是多少元;
(2)当B品牌粽子销售价为每袋54元时,每天可售出20袋,为了促销,该超市决定对B品牌粽子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋.当B品牌粽子每袋的销售价降低多少元时,每天售出B品牌粽子所获得的利润最大?最大利润是多少元?
【详解】(1)解:设A种品牌粽子每袋的进价是x元,B种品牌粽子每袋的进价是y元,
根据题意得,,
解得,
故A种品牌粽子每袋的进价是25元,B种品牌粽子每袋的进价是30元;
(2)解:设B品牌粽子每袋的销售价降低a元,利润为w元,
根据题意得,
w=(54-a-30)(20+5a)=-5a2+100a+480=-5(x-10)2+980,
∵-5<0,
∴当B品牌粽子每袋的销售价降低10元时,每天售出B品牌粽子所获得的利润最大,最大利润是980元.
课堂小结
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总销量=总售价-总成本.
确定自变量的取值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
确定最大利润
利用配方法或公式求最大值或利用函数简图和性质求出.
第二章 二次函数
2.4 二次函数的应用
第2课时 利润最大问题
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、熟练掌握用二次函数的性质求出商品利润的最大值问题,学会根据具体情况,由二次函数的性质,表示出正确的最大值;
2、学会根据实际问题的自变量的取值范围求出符合条件的商品利润具体值,可以准确掌握二次函数的实际应用;
导入新课
观察与思考
赶集,是中国一直以来就有的传统,尤其是过年期间,更是热闹!
思考:商品买卖过程中,作为商家利润最大化是永恒的追求.如果你是商家,如何定价才能获得最大利润呢?
讲授新课
知识点一 根据题意表示出利润问题中的数量关系
某商品现在的售价为每件100元,每星期可卖出300件,已知商品的进价为每件60元,则每星期销售额是 元,销售利润 元.
探究交流
30000
12000
数量关系
(1)销售额= 售价×销售量;
(2)利润= 销售额-总成本=单件利润×销售量;
(3)单件利润=售价-进价.
知识点二 利润最大问题解决思路
例1 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
涨价销售
①每件涨价x元,则每星期售出商品的利润y元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
涨价销售
20
300
20+x
300-10x
y=(20+x)(300-10x)
建立函数关系式:y=(20+x)(300-10x),
即:y=-10x2+100x+6000.
6000
②自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
当 时,y=-10×52+100×5+6000=6250.
即涨价5元时,最大利润是6250元.
降价销售
①每件降价x元,则每星期售出商品的利润y元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
降价销售
20
300
20-x
300+18x
y=(20-x)(300+18x)
建立函数关系式:y=(20-x)(300+18x),
即:y=-18x2+60x+6000.
例2 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
6000
综合可知,应定价58元时,才能使利润最大。
②自变量x的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤20.
③降价多少元时,利润最大,是多少?
当 时,
即降价 元时,最大利润是6050元.
即:y=-18x2+60x+6000,
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗
知识要点
求解最大利润问题的一般步骤
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润
×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
y=(160+10x)(120-6x)
例3 某旅馆有客房120间,每间房的日租金为160元,每天都客满.经市场调查,如果一间客房日租金每增加10元,则客房每天少出租6间,不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高?最高总收入是多少?
解:设每间客房的日租金提高10x元,则每天客房出租数会
减少6x间,设客房日租金为y万元,则
当x=2时,y有最大值,且y最大=19440.
答:每间客房的日租金提高到180元时,客房日租金的总收入
最高,最大收入为19440.
=-60(x-2)2+19440.
∵x≥0,且120-6x>0,
∴0≤x<20.
这时每间客房的日租金为160+10×2=180(元).
当堂练习
1.将进货单价为30元的某种商品按零售价100元1件卖出时,每天能卖出20件.若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1件,为了获得最大的利润,则应降价( )
A.5元 B.15元 C.25元 D.35元
【答案】C
【详解】解:设应降价x元,根据题意得,
y=(100-x-30)(20+x)=-x2+50x+1400=-(x-25)2+2025.
∵-1<0,
∴ 当x=25时,y取得最大值,
为了获得最大的利润,则应降价25元.
故选C.
2.某景区旅店有30张床位,每床每天收费10元时,可全部租出,若每床每天收费提高10元,则有2张床位不能租出;若每床每天收费再提高10元,则再有2张床位不能租出;若每次按提高10元的这种方法变化下去,则该旅店每天营业收入最多为( )
A.3125元 B.3120元 C.2950元 D.1280元
【答案】D
【详解】解:设每床每晚收费提高x个10元,旅店每天营业收入为y元,
根据题意得:
y=(10+10x)(30-2x)
=-20x2+280x+300
=-20(x-7)2+1280
∴当x=7时,y最大,最大值为1280元,
∴该旅店每天营业收入最多为1280元,
故选:D.
3.某服装店购进单价为15元的童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,为使该服装店平均每天的销售利润最大,则每件的定价为( )
A.21元 B.22元 C.23元 D.24元
【答案】B
【详解】解:设每天的销售利润为w元,每件的定价为x元,则每件的利润为(x-15)元,平均每天售出8+件, 根据题意得:
y=(x-15)(-2x+58)=-2x2+88x-870=-2(x-22)2+98,
∵ -2<0
∴当x=22时, w最大,
即每件的定价为22元时,每天的销售利润最大.
故选:B
4.某超市销售一种商品,每件成本为50元,销售人员经调查发现,该商品每月的销售量y(件)与销售单价x(元)之间满足函数关系式y=-5x+550,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.90元,4500元 B.80元,4500元
C.90元,4000元 D.80元,4000元
【答案】B
【详解】解:设每月总利润为w,
依题意得:w=y(x-50)
=(-5x+550)(x-50)
=-5x2+800x-27500
=-5(x-80)2+4500
∵-5<0,此图象开口向下,又x≥50,
∴当x=80时,w有最大值,最大值为4500元.
故选:B.
5.某件商品的销售利润y(元)与商品单价x(元)之间满足y=-x2+6x-7,不考虑其他因素,该商品的单价定为__________元时,销售一件该商品获得的利润最大,最大利润为__________元.
【答案】 3 2
【详解】解:∵某件商品的销售利润y(元)与商品单价x(元)之间满足
y=-x2+6x-7=-(x-3)2+2,a=-1<0,
∴该商品的单价定为3元时,销售一件该商品获得的利润最大,最大利润为2元,
故答案为:3;2.
6.某服装店销售一批服装,平均每天可售出20件,每件盈利40元,为了扩大销售,尽快减少库存,商店决定采取适当的降价措施,经市场调查发现,如果一件衣服每降价1元,商店平均每天可多售出2件,则每件衣服降价___________元时,服装店每天盈利最多.
【答案】15
【详解】解:设每件衣服降价x元,获得的总利润为y元,
由题意得:y=(40-x)(20+2x),
整理得:y=-2x2+60x+800=-2(x-15)2+1250,
∴当x=15时,y取得最大值;
故答案为:15.
7.某果园有100棵苹果树,平均每棵树可结660个苹果,根据经验估计,在这个果园里每多种一棵树,平均每棵树就会少结6个苹果,则果园里增____棵苹果树,所结苹果的总数最多.
【答案】5
【详解】解:设果园里增x棵苹果树,所结苹果的总数为y,
根据题意得y=(100+x)(660﹣6x)
=﹣6x2+60x+66000
=﹣6(x﹣5)2+66150,
∵a=﹣6,
∴当x=5时,y有最大值66150,
即果园里增5棵苹果树,所结苹果的总数最多.
故答案为5.
8.某企业研发出了一种新产品准备销售,已知研发、生产这种产品的成本为30元/件,据调查年销售量y(万件)关于售价x(元/件)的函数解析式为: ,则当该产品的售价x为________.(元/件)时,企业销售该产品获得的年利润最大.
【答案】50
【详解】解:设企业销售该产品获得的年利润为w元,根据题意得:
当40≤x<60时,
w=(x-30)(-2x+140)=-2x2+200x-4200=-2(x-50)2+800,
∵-2<0,
∴当x=50时,w有最大值,最大值为800;
当60≤x≤70时,
w=(x-30)(-x+80)=-x2+110x-2400=-(x-55)2+625,
∵-1<0,
∴当x>55时,w随x的增大而减小,
∴当x=60时,w有最大值,最大值为600;
∵800>600,
∴当x=50时,w有最大值,
即当该产品的售价x为50(元/件)时,企业销售该产品获得的年利润最大.
故答案为:50
9.超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间满足一次函数关系(其中10<x<25,且x为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.
(1)求y与x之间的函数关系式;
(2)设超市销售该品牌洗手液每天销售利润为w元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
【答案】(1)y=-5x+150(10<x<25)
(2)当每瓶洗手液的售价定为20元时,利润最大,最大利润是500元.
【详解】(1)解:设y=kx+b,
由题意得:,解得:,
∴y=-5x+150(10<x<25);
(2)解:由题意得:
w=(x-10)(-5x+150)
=-5x2+200x-1500
=-5(x-20)2+500
∵a=-5<0,抛物线开口朝下,w有最大值,
∵10<x<25,
∴当x=20时,w有最大值:500;
∴当每瓶洗手液的售价定为20元时,利润最大,最大利润是500元.
10.端午节前夕,某超市从厂家分两次购进A、B两种品牌的粽子,两次进货时,两种品牌粽子的进价不变.第一次购进A品牌粽子100袋和B品牌粽子150袋,总费用为7000元;第二次购进A品牌粽子180袋和B品牌粽子120袋,总费用为8100元.
(1)求A、B两种品牌粽子每袋的进价各是多少元;
(2)当B品牌粽子销售价为每袋54元时,每天可售出20袋,为了促销,该超市决定对B品牌粽子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋.当B品牌粽子每袋的销售价降低多少元时,每天售出B品牌粽子所获得的利润最大?最大利润是多少元?
【详解】(1)解:设A种品牌粽子每袋的进价是x元,B种品牌粽子每袋的进价是y元,
根据题意得,,
解得,
故A种品牌粽子每袋的进价是25元,B种品牌粽子每袋的进价是30元;
(2)解:设B品牌粽子每袋的销售价降低a元,利润为w元,
根据题意得,
w=(54-a-30)(20+5a)=-5a2+100a+480=-5(x-10)2+980,
∵-5<0,
∴当B品牌粽子每袋的销售价降低10元时,每天售出B品牌粽子所获得的利润最大,最大利润是980元.
课堂小结
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总销量=总售价-总成本.
确定自变量的取值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
确定最大利润
利用配方法或公式求最大值或利用函数简图和性质求出.
