专题3.7 切线长定理 课件(共34张PPT)
文档属性
| 名称 | 专题3.7 切线长定理 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 00:00:00 | ||
图片预览






文档简介
(共34张PPT)
第三章 圆
3.7 切线长定理
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、理解切线长的概念和定理,学会判定圆的切线,并且求出切线的长;
2、利用切线长定理证明与圆切线相关的几何题;
3、掌握切线长定理与圆其他知识点的综合应用;
导入新课
观察与思考
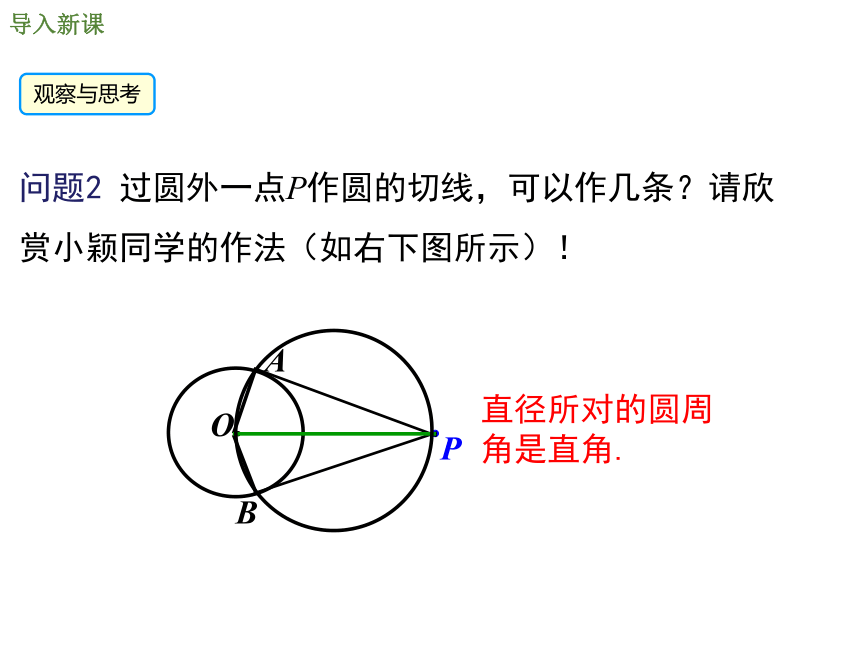
问题2 过圆外一点P作圆的切线,可以作几条?请欣赏小颖同学的作法(如右下图所示)!
O.
P
A
B
直径所对的圆周角是直角.
讲授新课
知识点一 切线长的概念和切线的定理
P
1.切线长的定义:
经过圆外一点作圆的切线,这点和切点之间的线段的长叫作切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
2.切线长与切线的区别在哪里?
合作探究
B
P
O
A
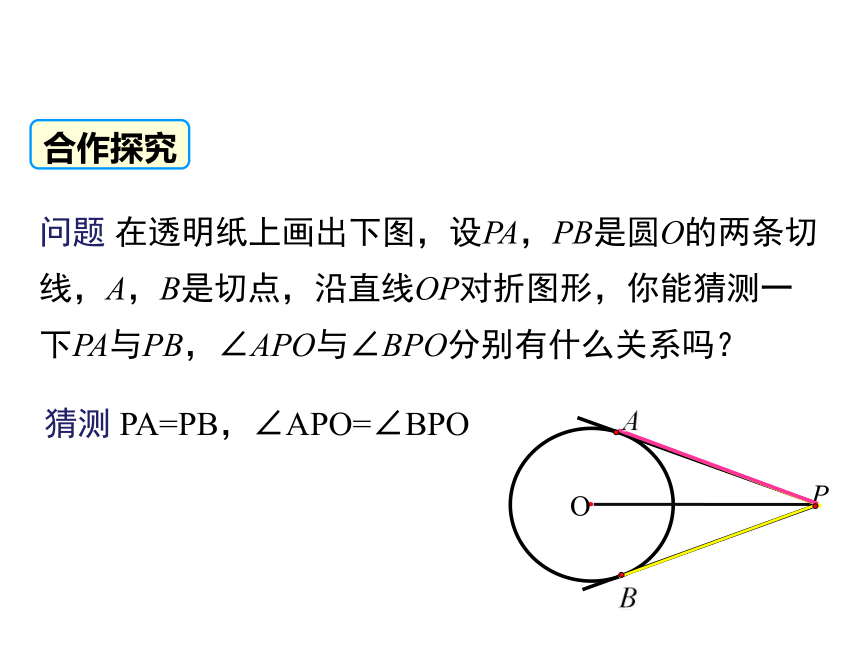
问题 在透明纸上画出下图,设PA,PB是圆O的两条切线,A,B是切点,沿直线OP对折图形,你能猜测一下PA与PB,∠APO与∠BPO分别有什么关系吗?
猜测 PA=PB,∠APO=∠BPO
推导与验证
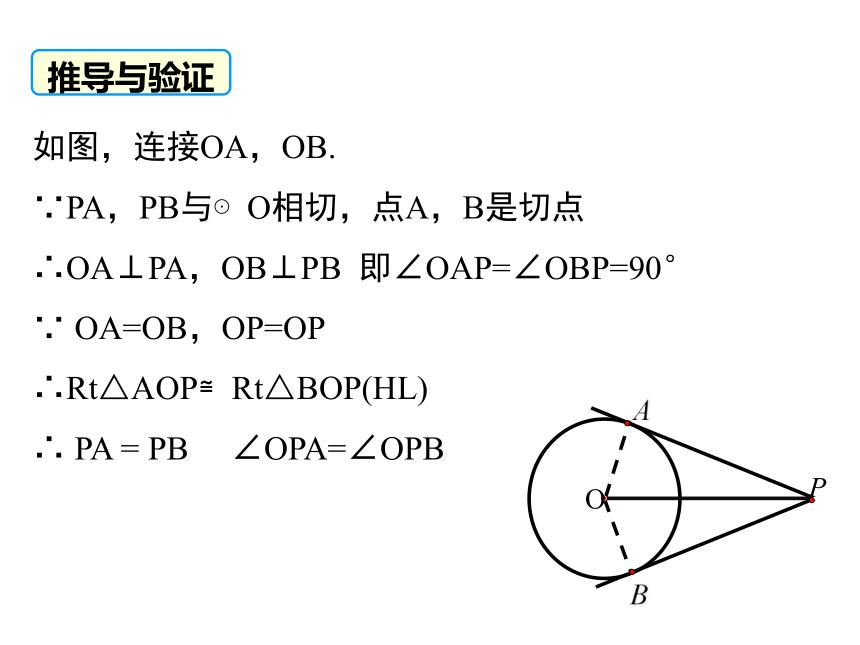
如图,连接OA,OB.
∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB
B
P
O
A
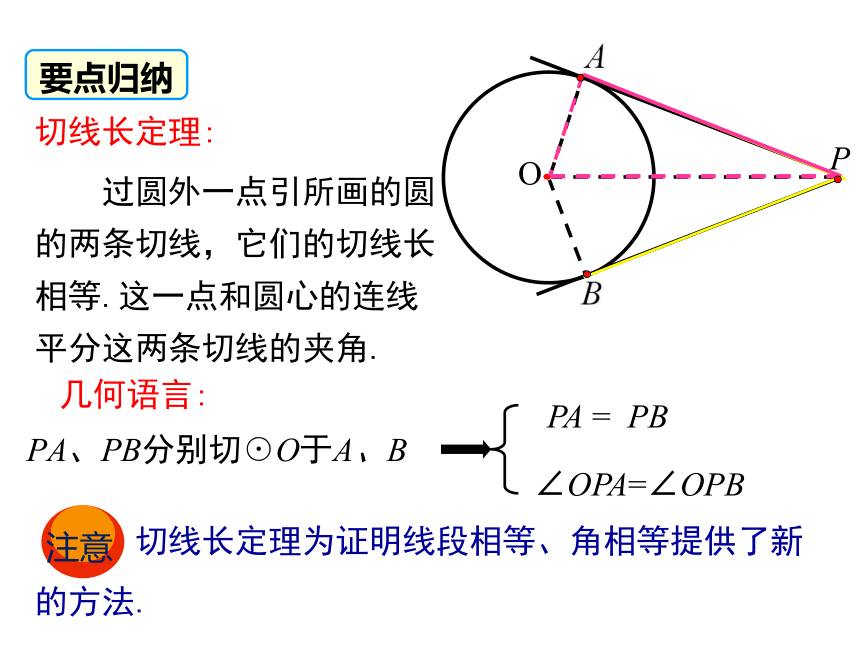
切线长定理:
过圆外一点引所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
切线长定理为证明线段相等、角相等提供了新的方法.
注意
要点归纳
B
P
O
A
O
P
A
B
C
E
D
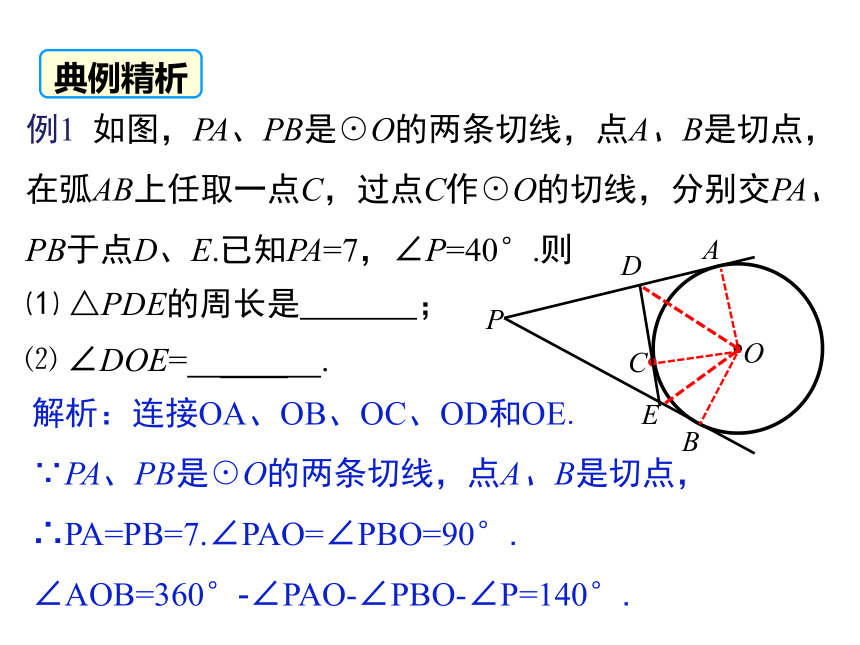
解析:连接OA、OB、OC、OD和OE.
∵PA、PB是☉O的两条切线,点A、B是切点,∴PA=PB=7.∠PAO=∠PBO=90°. ∠AOB=360°-∠PAO-∠PBO-∠P=140°.
⑴ △PDE的周长是 ;
例1 如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E.已知PA=7,∠P=40°.则
⑵ ∠DOE= ____ .
典例精析
又∵DC、DA是☉O的两条切线,点C、A是切点,∴DC=DA.同理可得CE=EB.
l△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.
O
P
A
B
C
E
D
∵OA=OC,OD=OD,∴△AOD≌△COD,
∴∠DOC=∠DOA= ∠AOC.
同理可得∠COE= ∠COB.
∠DOE=∠DOC+∠COE= (∠AOC+
∠COB)=70°.
切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
方法归纳
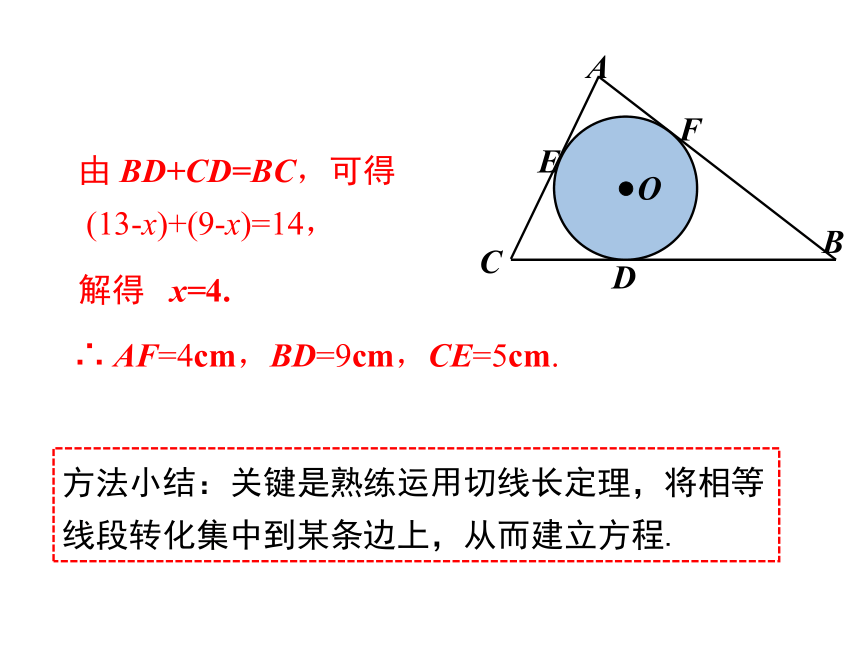
例2 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=(9-x)cm,
BF=BD=AB-AF=(13-x)cm.
想一想:图中你能找出哪些相等的线段?理由是什么?
A
C
B
E
D
F
O
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF=4cm,BD=9cm,CE=5cm.
方法小结:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
解得 x=4.
A
C
B
E
D
F
O
当堂练习
1.如图,○O与正方形ABCD的两边AB、AD相切,且DE与○O相切于E点.若○O的半径为4,且AB=10,则DE的长度为( )
A.5 B.6 C. D.
【答案】B
【分析】连接OE,OF,OG,根据切线性质证四边形ABCD为正方形,根据正方形性质和切线长性质可得DE=DF.
【点睛】本题考查了切线和切线长定理,作辅助线,利用切线长性质求解是关键.
2.如图,⊙O是Rt△ABC的内切圆,D,E,F分别为切点,且∠C=90°.已知AC=12,BC=5,则四边形OFCE的面积为( )
A.1 B.15 C. D.4
【答案】D
【分析】先根据勾股定理求出AB的长,再连接OD,设半径为r,再根据切线长定理,AF=AD,BE=BD,AD+BD=AB,得到关于r的方程,解方程,即可求出四边形OFCE的面积.
3.如图,P为○O外一点,PA、PB分别切圆O于点A、B,CD切○O于点E,分别交PA、PB于点C、D,若△PCD的周长为18,则PA的长度为( )
A.7 B.9 C.12 D.14
【答案】B
【分析】先根据切线长定理得到PA=PB,CA=CE,DE=DB,再利用△PCD的周长为18得到PC+CE+DE+PD=18,然后利用等线段代换得到PA+PB=18,从而得到PA的长.
【点睛】本题考查了切线的性质,利用运用切线长定理是解决问题的关键.
4.如图,○O的半径是1,点P是直线y=-x+2上一动点,过点P作○O的切线,切点为A,连接OA,OP,则AP的最小值为( ).
A. B.1 C. D.
【答案】B
【分析】根据题意设P(a,-a+2),则OP的长可以表示出来,根据圆O的半径是1得OA=1,根据AP是圆O的切线得∠OAP=90°,即可得△OAP是直角三角形,在Rt△OAP中,根据勾股定理得AP2=OP2-OA2,即可得AP2的值,根据二次函数的性质得当a-1=0时,AP有最小值,即可得.
5.如图,PA,PB分别与○O相切于点A,B ,直线EF与○O相切于点C,分别交PA,PB于E,F,且PA=4,则△PEF的周长为______cm.
【答案】8
【分析】根据切线长定理可知AE=CE、BE=CF,进而可求出结果;
【详解】解:∵PA,PB分别与○O相切;
∴ PA=PB=4(cm)
∵EC、EA分别与○O相切
∴AE=CE
同理:BF=CF
∴ C△PEF=8
故答案为:8
6.如图,○O是三角形纸片ABC的内切圆,在○O的右侧沿着○O相切的直线MN剪下△AMN.若△ABC的周长为15cm,BC=4cm,则剪下的△AMN的周长为________cm.
【答案】7
【分析】根据切线长定理求得BC+BD+CE=2BC=8,MN+MA+AN=AD+AE=15-8=7,即可求解.
【详解】解:∵○O是三角形纸片ABC的内切圆,MN与○O相切,
∴BC+BD+CE=2BC=8,MN+MA+AN=AD+AE=15-8=7,
即剪下的△AMN的周长为7cm,
故答案为:7.
7.如图,○O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=12,则BF=_______.
【答案】10
【分析】设BF=BD=x,利用切线长定理,构建方程解决问题即可.
【点睛】本题考查三角形的内心,勾股定理,切线长定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
8.如图,PA和PB是圆O的两条切线,A,B是切点.C是弧AB上任意一点,过点C画○O的切线,分别交PA和PB于D,E两点,已知PA=PB=5cm,则△PDE的周长为___________cm.
【答案】10
【详解】解:∵PA和PB是圆O的两条切线,
∴PA=PB,
同理可得:DA=DC,EB=EC,
∴△PDE的周长
=PD+DE+PE
=PD+DC+EC+PE=PD+DA+EB+PE
=PA+PB=10(cm).
故答案为:10.
9.如图,AB是圆O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求圆O的半径.
【答案】(1)见解析
(2)5
【分析】(1)根据DF⊥CG,CD⊥AB可得∠D=∠G,再由圆周角定理可得∠A=∠D,从而得到∠A=∠G,即可求证;
(2)连接OC,根据等腰三角形的性质和垂径定理可得AE=EG=8,EC=ED=4,然后在Rt△OEC中,由勾股定理,即可求解.
10.如图,线段AB是⊙O的直径,⊙O交线段BC于D,且D是BC的中点,DE⊥AC于E,连接AD.
(1)求证:DE是⊙O的切线;
(2)若AE=1,AB=4,求AD的长
证明:连接OD,
则:OA=OD,∠ODA=∠OAD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,∠B+∠ABD=90°
∴∠CDE+∠EDA=90°
又∵D是BC的中点,
∴AC=AB,
∴∠C=∠B,
∵DE⊥AC
∴∠C+∠CDE=90°
∴∠CDE=∠BAD,
又∵∠ODA=∠OAD,∠CDE+∠EDA=90°,
∴∠ODA+∠EDA=90DU3,即:∠ODE=90°,
∴OD⊥DE
∴DE是⊙O的切线.
解:∵∠CDA=∠CED=90°,∠CAD=∠CAD,
∴,
∴AD2=AE·AC,
∴AC=AB=4,
∴AD2=1×4=4,
∴AD=2或AD=-2(舍);
∴AD的长为2.
课堂小结
切线长
切线长定理
作用
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
三角形内切圆
运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
应用
重要结论
只适合于直角三角形
第三章 圆
3.7 切线长定理
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、理解切线长的概念和定理,学会判定圆的切线,并且求出切线的长;
2、利用切线长定理证明与圆切线相关的几何题;
3、掌握切线长定理与圆其他知识点的综合应用;
导入新课
观察与思考
问题2 过圆外一点P作圆的切线,可以作几条?请欣赏小颖同学的作法(如右下图所示)!
O.
P
A
B
直径所对的圆周角是直角.
讲授新课
知识点一 切线长的概念和切线的定理
P
1.切线长的定义:
经过圆外一点作圆的切线,这点和切点之间的线段的长叫作切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
2.切线长与切线的区别在哪里?
合作探究
B
P
O
A
问题 在透明纸上画出下图,设PA,PB是圆O的两条切线,A,B是切点,沿直线OP对折图形,你能猜测一下PA与PB,∠APO与∠BPO分别有什么关系吗?
猜测 PA=PB,∠APO=∠BPO
推导与验证
如图,连接OA,OB.
∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB
B
P
O
A
切线长定理:
过圆外一点引所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
切线长定理为证明线段相等、角相等提供了新的方法.
注意
要点归纳
B
P
O
A
O
P
A
B
C
E
D
解析:连接OA、OB、OC、OD和OE.
∵PA、PB是☉O的两条切线,点A、B是切点,∴PA=PB=7.∠PAO=∠PBO=90°. ∠AOB=360°-∠PAO-∠PBO-∠P=140°.
⑴ △PDE的周长是 ;
例1 如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E.已知PA=7,∠P=40°.则
⑵ ∠DOE= ____ .
典例精析
又∵DC、DA是☉O的两条切线,点C、A是切点,∴DC=DA.同理可得CE=EB.
l△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.
O
P
A
B
C
E
D
∵OA=OC,OD=OD,∴△AOD≌△COD,
∴∠DOC=∠DOA= ∠AOC.
同理可得∠COE= ∠COB.
∠DOE=∠DOC+∠COE= (∠AOC+
∠COB)=70°.
切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
方法归纳
例2 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=(9-x)cm,
BF=BD=AB-AF=(13-x)cm.
想一想:图中你能找出哪些相等的线段?理由是什么?
A
C
B
E
D
F
O
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF=4cm,BD=9cm,CE=5cm.
方法小结:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
解得 x=4.
A
C
B
E
D
F
O
当堂练习
1.如图,○O与正方形ABCD的两边AB、AD相切,且DE与○O相切于E点.若○O的半径为4,且AB=10,则DE的长度为( )
A.5 B.6 C. D.
【答案】B
【分析】连接OE,OF,OG,根据切线性质证四边形ABCD为正方形,根据正方形性质和切线长性质可得DE=DF.
【点睛】本题考查了切线和切线长定理,作辅助线,利用切线长性质求解是关键.
2.如图,⊙O是Rt△ABC的内切圆,D,E,F分别为切点,且∠C=90°.已知AC=12,BC=5,则四边形OFCE的面积为( )
A.1 B.15 C. D.4
【答案】D
【分析】先根据勾股定理求出AB的长,再连接OD,设半径为r,再根据切线长定理,AF=AD,BE=BD,AD+BD=AB,得到关于r的方程,解方程,即可求出四边形OFCE的面积.
3.如图,P为○O外一点,PA、PB分别切圆O于点A、B,CD切○O于点E,分别交PA、PB于点C、D,若△PCD的周长为18,则PA的长度为( )
A.7 B.9 C.12 D.14
【答案】B
【分析】先根据切线长定理得到PA=PB,CA=CE,DE=DB,再利用△PCD的周长为18得到PC+CE+DE+PD=18,然后利用等线段代换得到PA+PB=18,从而得到PA的长.
【点睛】本题考查了切线的性质,利用运用切线长定理是解决问题的关键.
4.如图,○O的半径是1,点P是直线y=-x+2上一动点,过点P作○O的切线,切点为A,连接OA,OP,则AP的最小值为( ).
A. B.1 C. D.
【答案】B
【分析】根据题意设P(a,-a+2),则OP的长可以表示出来,根据圆O的半径是1得OA=1,根据AP是圆O的切线得∠OAP=90°,即可得△OAP是直角三角形,在Rt△OAP中,根据勾股定理得AP2=OP2-OA2,即可得AP2的值,根据二次函数的性质得当a-1=0时,AP有最小值,即可得.
5.如图,PA,PB分别与○O相切于点A,B ,直线EF与○O相切于点C,分别交PA,PB于E,F,且PA=4,则△PEF的周长为______cm.
【答案】8
【分析】根据切线长定理可知AE=CE、BE=CF,进而可求出结果;
【详解】解:∵PA,PB分别与○O相切;
∴ PA=PB=4(cm)
∵EC、EA分别与○O相切
∴AE=CE
同理:BF=CF
∴ C△PEF=8
故答案为:8
6.如图,○O是三角形纸片ABC的内切圆,在○O的右侧沿着○O相切的直线MN剪下△AMN.若△ABC的周长为15cm,BC=4cm,则剪下的△AMN的周长为________cm.
【答案】7
【分析】根据切线长定理求得BC+BD+CE=2BC=8,MN+MA+AN=AD+AE=15-8=7,即可求解.
【详解】解:∵○O是三角形纸片ABC的内切圆,MN与○O相切,
∴BC+BD+CE=2BC=8,MN+MA+AN=AD+AE=15-8=7,
即剪下的△AMN的周长为7cm,
故答案为:7.
7.如图,○O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=12,则BF=_______.
【答案】10
【分析】设BF=BD=x,利用切线长定理,构建方程解决问题即可.
【点睛】本题考查三角形的内心,勾股定理,切线长定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
8.如图,PA和PB是圆O的两条切线,A,B是切点.C是弧AB上任意一点,过点C画○O的切线,分别交PA和PB于D,E两点,已知PA=PB=5cm,则△PDE的周长为___________cm.
【答案】10
【详解】解:∵PA和PB是圆O的两条切线,
∴PA=PB,
同理可得:DA=DC,EB=EC,
∴△PDE的周长
=PD+DE+PE
=PD+DC+EC+PE=PD+DA+EB+PE
=PA+PB=10(cm).
故答案为:10.
9.如图,AB是圆O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求圆O的半径.
【答案】(1)见解析
(2)5
【分析】(1)根据DF⊥CG,CD⊥AB可得∠D=∠G,再由圆周角定理可得∠A=∠D,从而得到∠A=∠G,即可求证;
(2)连接OC,根据等腰三角形的性质和垂径定理可得AE=EG=8,EC=ED=4,然后在Rt△OEC中,由勾股定理,即可求解.
10.如图,线段AB是⊙O的直径,⊙O交线段BC于D,且D是BC的中点,DE⊥AC于E,连接AD.
(1)求证:DE是⊙O的切线;
(2)若AE=1,AB=4,求AD的长
证明:连接OD,
则:OA=OD,∠ODA=∠OAD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,∠B+∠ABD=90°
∴∠CDE+∠EDA=90°
又∵D是BC的中点,
∴AC=AB,
∴∠C=∠B,
∵DE⊥AC
∴∠C+∠CDE=90°
∴∠CDE=∠BAD,
又∵∠ODA=∠OAD,∠CDE+∠EDA=90°,
∴∠ODA+∠EDA=90DU3,即:∠ODE=90°,
∴OD⊥DE
∴DE是⊙O的切线.
解:∵∠CDA=∠CED=90°,∠CAD=∠CAD,
∴,
∴AD2=AE·AC,
∴AC=AB=4,
∴AD2=1×4=4,
∴AD=2或AD=-2(舍);
∴AD的长为2.
课堂小结
切线长
切线长定理
作用
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
三角形内切圆
运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
应用
重要结论
只适合于直角三角形
