沪科版八年级上册数学 14全等三角形 复习 教案
文档属性
| 名称 | 沪科版八年级上册数学 14全等三角形 复习 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 819.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览



文档简介
全等三角形(复习课)
教学目标
1、熟悉巩固全等三角形的定义、性质、判定,角平分线的性质、判定。
2、熟练掌握三角形全等、角平分线相关证明的思路、方法、技巧,着力解决学生分析问题解决问题的能力。
教学重难点:
三角形全等、角平分线的性质、判定的合理灵活运用,分析解决能力的提升。
教学过程:
一、全等三角形
1.什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?
能够完全重合的两个三角形叫做全等三角形。一个三角形经过平移、翻折、旋转可以得到它的全等形。
2:全等三角形有哪些性质?
(1)全等三角形的对应边相等、对应角相等。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
知识回顾:
一般三角形 ( 全等三角形的复习.pub ) ( 全等三角形的复习.pub )全等的条件 ( 全等三角形的复习.pub ):
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:HL
三角形全等的判定方法:
边边边:三边对应相等的两个三角形全等(可简写成“SSS”)
边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)
角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)
角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)
斜边.直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”)
方法指引
证明两个三角形全等的基本思路:
1:已知两边---A找第三边 (SSS) B找夹角(SAS) C找是否有直角 (HL)
2:已知一边一角---(1)已知一边和它的邻角: A找这边的另一个邻角(ASA) B找这个角的另一个边(SAS) C找这边的对角(AAS)
(2)已知一边和它的对角:A找一角(AAS) B已知角是直角,找一边(HL)
3:已知两角-A找两角的夹边(ASA) B找夹边外的任意边(AAS)
练习
1.证明两个三角形全等,要结合题目的条件和结论,选择恰当的判定方法
2.全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
总之,证明过程中能用简单方法的就不要绕弯路。
二、角的平分线
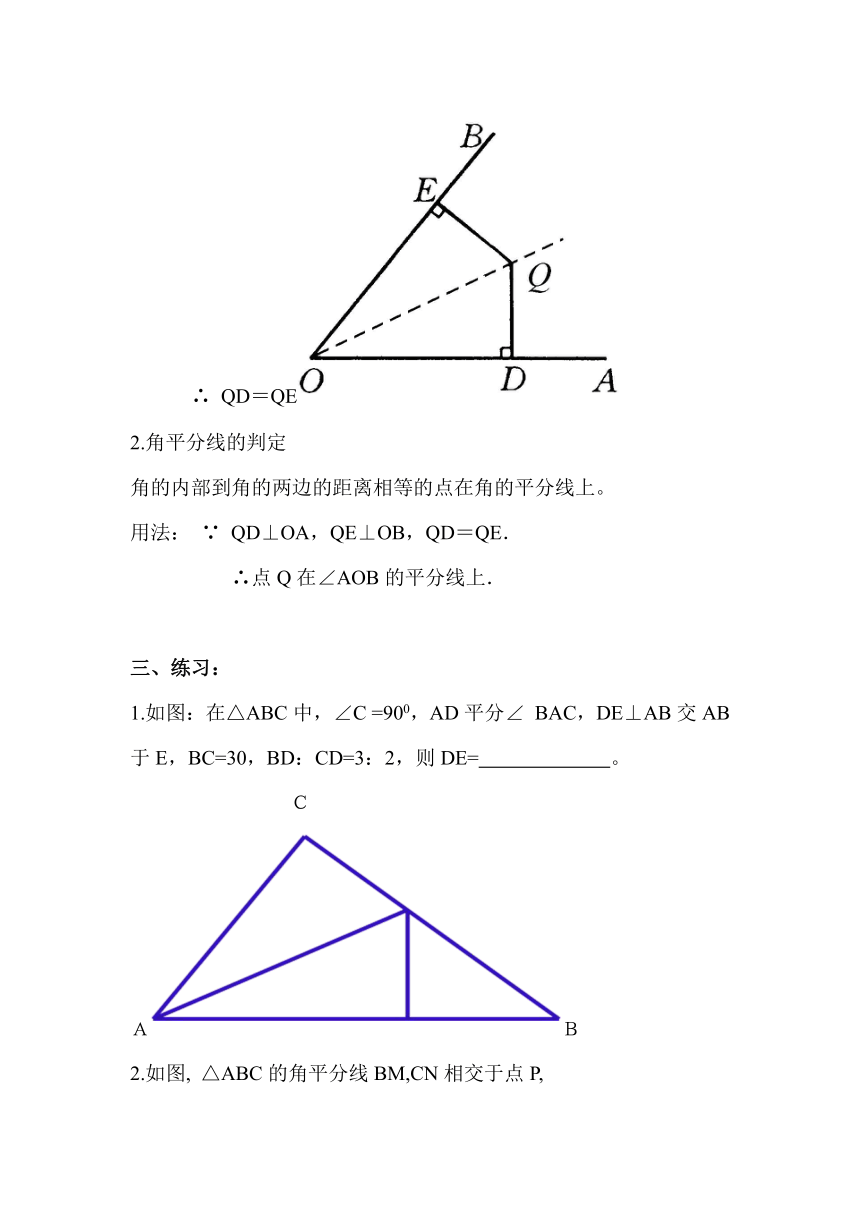
1.角平分线的性质:
角的平分线上的点到角的两边的距离相等.
用法:∵ QD⊥OA,QE⊥OB,
点Q在∠AOB的平分线上
∴ QD=QE
2.角平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上。
用法: ∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
三、练习:
1.如图:在△ABC中,∠C =900,AD平分∠ BAC,DE⊥AB交AB于E,BC=30,BD:CD=3:2,则DE= 。
C
AB
2.如图, △ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB、BC、CA的距离相等
3.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
4.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
变式:以上条件不变,将△ABC绕点C旋转一定角度(大于零度而小于六十度),以上的结论海成立吗?
5:如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?
练习
6:如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。(只写出一种情况)①AB=AC ②DE=DF ③BE=CF
已知: EG∥AF
求证:
拓展题
7.如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.
求证:BC∥EF
拓展题
8.如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,则AB与AC+BD相等吗?请说明理由。
要证明两条线段的和与一条线段相等时常用的两种方法:
1、可在长线段上截取与两条线段中一条相等的一段,然后证明剩余的线段与另一条线段相等。(割)
2、把一个三角形移到另一位置,使两线段补成一条线段,再证明它与长线段相等。(补)
总结提高
学习全等三角形应注意以下几个问题:
(1):要正确区分“对应边”与“对边”,“对应角”与 “对角”的不同含义;
(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
(4):时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”
教学目标
1、熟悉巩固全等三角形的定义、性质、判定,角平分线的性质、判定。
2、熟练掌握三角形全等、角平分线相关证明的思路、方法、技巧,着力解决学生分析问题解决问题的能力。
教学重难点:
三角形全等、角平分线的性质、判定的合理灵活运用,分析解决能力的提升。
教学过程:
一、全等三角形
1.什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?
能够完全重合的两个三角形叫做全等三角形。一个三角形经过平移、翻折、旋转可以得到它的全等形。
2:全等三角形有哪些性质?
(1)全等三角形的对应边相等、对应角相等。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
知识回顾:
一般三角形 ( 全等三角形的复习.pub ) ( 全等三角形的复习.pub )全等的条件 ( 全等三角形的复习.pub ):
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:HL
三角形全等的判定方法:
边边边:三边对应相等的两个三角形全等(可简写成“SSS”)
边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)
角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)
角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)
斜边.直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”)
方法指引
证明两个三角形全等的基本思路:
1:已知两边---A找第三边 (SSS) B找夹角(SAS) C找是否有直角 (HL)
2:已知一边一角---(1)已知一边和它的邻角: A找这边的另一个邻角(ASA) B找这个角的另一个边(SAS) C找这边的对角(AAS)
(2)已知一边和它的对角:A找一角(AAS) B已知角是直角,找一边(HL)
3:已知两角-A找两角的夹边(ASA) B找夹边外的任意边(AAS)
练习
1.证明两个三角形全等,要结合题目的条件和结论,选择恰当的判定方法
2.全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
总之,证明过程中能用简单方法的就不要绕弯路。
二、角的平分线
1.角平分线的性质:
角的平分线上的点到角的两边的距离相等.
用法:∵ QD⊥OA,QE⊥OB,
点Q在∠AOB的平分线上
∴ QD=QE
2.角平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上。
用法: ∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
三、练习:
1.如图:在△ABC中,∠C =900,AD平分∠ BAC,DE⊥AB交AB于E,BC=30,BD:CD=3:2,则DE= 。
C
AB
2.如图, △ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB、BC、CA的距离相等
3.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
4.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
变式:以上条件不变,将△ABC绕点C旋转一定角度(大于零度而小于六十度),以上的结论海成立吗?
5:如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?
练习
6:如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。(只写出一种情况)①AB=AC ②DE=DF ③BE=CF
已知: EG∥AF
求证:
拓展题
7.如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.
求证:BC∥EF
拓展题
8.如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,则AB与AC+BD相等吗?请说明理由。
要证明两条线段的和与一条线段相等时常用的两种方法:
1、可在长线段上截取与两条线段中一条相等的一段,然后证明剩余的线段与另一条线段相等。(割)
2、把一个三角形移到另一位置,使两线段补成一条线段,再证明它与长线段相等。(补)
总结提高
学习全等三角形应注意以下几个问题:
(1):要正确区分“对应边”与“对边”,“对应角”与 “对角”的不同含义;
(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
(4):时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”
