沪科版八年级上册数学 15.3.2利用等腰三角形的性质进行证明 教案
文档属性
| 名称 | 沪科版八年级上册数学 15.3.2利用等腰三角形的性质进行证明 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 57.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 10:49:40 | ||
图片预览


文档简介
利用等腰三角形的性质进行证明
教材分析:在上一课时学习等腰三角形的几个重要性质后,本课时教材主要引导学生利用上述性质进行有关证明。当然,在证明或解答有关数学问题的同时,也进一步巩固了全等三角形等知识内容。本节课教材内容设置的主要目的在于,如何通过运用等腰三角形的性质解决数学问题,进而寻求数学证明的一般思路和方法。
学情分析:在学习本节课之前,学生已经对等腰三角形的性质(包括等边三角形的性质)有了较好掌握,对全等三角形等相关知识内容已经能够较灵活地运用。以此为基础,加上教师的适当引导、合理启发、适时点拨,学生学习本节课的困难就不会太大。
教学目标:
1.知识与技能:掌握等腰三角形、等边三角形的性质及判定两个直角三角形全等的“HL”定理,能够灵活运用它们进行证明和计算;
2.过程与方法:经历利用等腰三角形的性质进行证明或计算的过程,体会问题解决策略的多样性,总结分析、解决问题的方法,感受数学结合等思想方法;
3.情感、态度和价值观:在富有挑战性、丰富多彩的数学活动中,激发学生的探索欲望,培养自主意识、合作意识与探究意识,树立学好数学的信心。
教学重点:利用等腰三角形的性质进行证明或计算。
教学难点:等腰三角形性质的灵活运用及与其他数学知识的综合运用。
教学准备:“几何画板”课件等。
教学过程:
一、回顾思考
师:同学们,上一节课,我们学习了等腰三角形的几个重要性质。大家还记得,都是如何叙述的吗?这节课,我们将利用等腰三角形的这些性质进行证明。(简要板书三个性质及课题:利用等腰三角形的性质进行证明)
生:回顾等腰三角形的性质,口答,准备进入良好学习探究状态。
设计意图:回顾等腰三角形的有关性质,以旧引新,激发学生的探究欲望,为利用等腰三角形的性质进行证明或计算做知识铺垫。
二、温故知新
师:结合“几何画板”演示,引导学生回顾“两边和其中一边的对角分别相等时,两个三角形不一定全等”这一情况。通过“拖动”,改变三角形形状,帮助学生发现,当“其中一边的对角是直角时,两个三角形全等”(即“HL”成立)。
生:与老师互动,观察演示,思考回顾,发现“一般”与“特殊”的关系,体会“变”与“不变”的奥妙。
师:顺势出示问题,求证:斜边和一条直角边分别相等的两个直角三角形全等。
生:在老师的启发引导下,在草稿纸上画图,口述“已知”、“求证”。
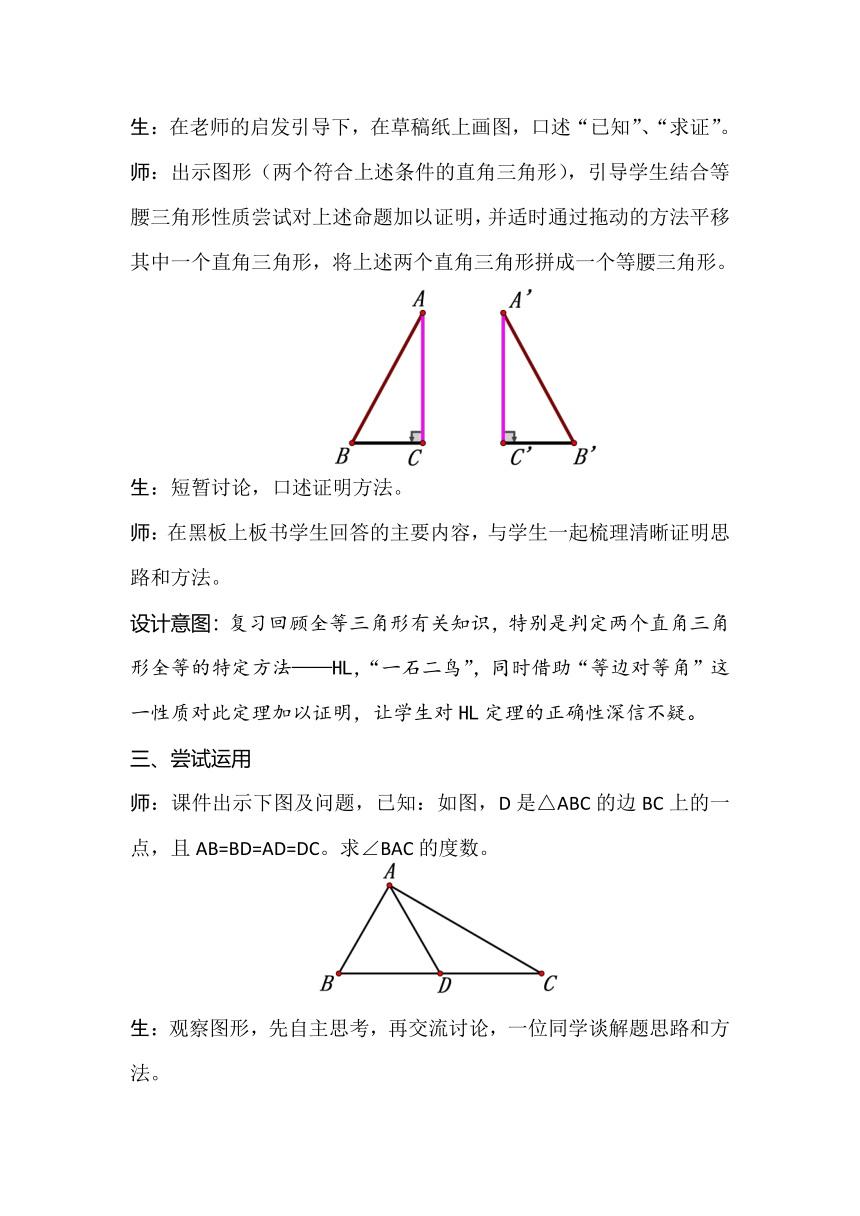
师:出示图形(两个符合上述条件的直角三角形),引导学生结合等腰三角形性质尝试对上述命题加以证明,并适时通过拖动的方法平移其中一个直角三角形,将上述两个直角三角形拼成一个等腰三角形。
生:短暂讨论,口述证明方法。
师:在黑板上板书学生回答的主要内容,与学生一起梳理清晰证明思路和方法。
设计意图:复习回顾全等三角形有关知识,特别是判定两个直角三角形全等的特定方法——HL,“一石二鸟”,同时借助“等边对等角”这一性质对此定理加以证明,让学生对HL定理的正确性深信不疑。
三、尝试运用
师:课件出示下图及问题,已知:如图,D是△ABC的边BC上的一点,且AB=BD=AD=DC。求∠BAC的度数。
生:观察图形,先自主思考,再交流讨论,一位同学谈解题思路和方法。
师:结合学生的解题思路分析,示范板书解题步骤。
设计意图:再次利用等腰三角形性质——“等边对等角”与等边三角形性质进行问题解决,规范解题步骤。
四、创新发散
师:出示以下证明题及图形,引导学生采取几种不同方法证明,已知:如图,点D,E在△ABC的底边BC上,AB=AC,AD=AE。 求证:BD=CE。
生:交流讨论,可能想到用全等三角形知识或等腰三角形的“三线合一”性等加以证明。(两位同学演板,其余同学自主完成,然后评析完善)
师:引导学生思考分析每种证明方法的优劣,进一步优化解题思路。
设计意图:进一步巩固应用等腰三角形性质及全等三角形判定方法,鼓励学生使用多种不同方法解决问题,一题多解,发散思维,培养学生思维的创造性与求异性。
五、转化提升
师:出示如下证明题及图形,引导学生转化,尽量用不同方法证明,如图,已知在△ABC中,AB=AC,BD⊥AC于D。求证:∠BAC=2∠DBC。
生:先自主思考,再集体讨论,然后两位同学分享解题方法。
师:板书学生回答的主要内容,共同评析学生的解题方法。
设计意图:再次利用等腰三角形的“三线合一”性解决问题,或综合利用“等边对等角”及三角形内角和定理解决问题,渗透转化思想,锻炼学生思维的灵活性与可逆性。
六、畅所欲言
师:本节课的学习活动即将结束,谈谈你的感想与收获吧!
生:梳理思路,畅谈本节课学习收获与感受,学会分享。
设计意图:引导学生梳理思路,从整体上建构本节课所学知识,反思自己的学习过程,发展有序思考及有条理地与表达能力。
七、作业布置
师:出示如下作业:1.教科书第136页第3、第4题;2.完成本课时《同步练习》。
生:记录,准备课余时间完成。
设计意图:进一步巩固本节课所学知识内容,将知识巩固与能力培养延伸到课外。
教材分析:在上一课时学习等腰三角形的几个重要性质后,本课时教材主要引导学生利用上述性质进行有关证明。当然,在证明或解答有关数学问题的同时,也进一步巩固了全等三角形等知识内容。本节课教材内容设置的主要目的在于,如何通过运用等腰三角形的性质解决数学问题,进而寻求数学证明的一般思路和方法。
学情分析:在学习本节课之前,学生已经对等腰三角形的性质(包括等边三角形的性质)有了较好掌握,对全等三角形等相关知识内容已经能够较灵活地运用。以此为基础,加上教师的适当引导、合理启发、适时点拨,学生学习本节课的困难就不会太大。
教学目标:
1.知识与技能:掌握等腰三角形、等边三角形的性质及判定两个直角三角形全等的“HL”定理,能够灵活运用它们进行证明和计算;
2.过程与方法:经历利用等腰三角形的性质进行证明或计算的过程,体会问题解决策略的多样性,总结分析、解决问题的方法,感受数学结合等思想方法;
3.情感、态度和价值观:在富有挑战性、丰富多彩的数学活动中,激发学生的探索欲望,培养自主意识、合作意识与探究意识,树立学好数学的信心。
教学重点:利用等腰三角形的性质进行证明或计算。
教学难点:等腰三角形性质的灵活运用及与其他数学知识的综合运用。
教学准备:“几何画板”课件等。
教学过程:
一、回顾思考
师:同学们,上一节课,我们学习了等腰三角形的几个重要性质。大家还记得,都是如何叙述的吗?这节课,我们将利用等腰三角形的这些性质进行证明。(简要板书三个性质及课题:利用等腰三角形的性质进行证明)
生:回顾等腰三角形的性质,口答,准备进入良好学习探究状态。
设计意图:回顾等腰三角形的有关性质,以旧引新,激发学生的探究欲望,为利用等腰三角形的性质进行证明或计算做知识铺垫。
二、温故知新
师:结合“几何画板”演示,引导学生回顾“两边和其中一边的对角分别相等时,两个三角形不一定全等”这一情况。通过“拖动”,改变三角形形状,帮助学生发现,当“其中一边的对角是直角时,两个三角形全等”(即“HL”成立)。
生:与老师互动,观察演示,思考回顾,发现“一般”与“特殊”的关系,体会“变”与“不变”的奥妙。
师:顺势出示问题,求证:斜边和一条直角边分别相等的两个直角三角形全等。
生:在老师的启发引导下,在草稿纸上画图,口述“已知”、“求证”。
师:出示图形(两个符合上述条件的直角三角形),引导学生结合等腰三角形性质尝试对上述命题加以证明,并适时通过拖动的方法平移其中一个直角三角形,将上述两个直角三角形拼成一个等腰三角形。
生:短暂讨论,口述证明方法。
师:在黑板上板书学生回答的主要内容,与学生一起梳理清晰证明思路和方法。
设计意图:复习回顾全等三角形有关知识,特别是判定两个直角三角形全等的特定方法——HL,“一石二鸟”,同时借助“等边对等角”这一性质对此定理加以证明,让学生对HL定理的正确性深信不疑。
三、尝试运用
师:课件出示下图及问题,已知:如图,D是△ABC的边BC上的一点,且AB=BD=AD=DC。求∠BAC的度数。
生:观察图形,先自主思考,再交流讨论,一位同学谈解题思路和方法。
师:结合学生的解题思路分析,示范板书解题步骤。
设计意图:再次利用等腰三角形性质——“等边对等角”与等边三角形性质进行问题解决,规范解题步骤。
四、创新发散
师:出示以下证明题及图形,引导学生采取几种不同方法证明,已知:如图,点D,E在△ABC的底边BC上,AB=AC,AD=AE。 求证:BD=CE。
生:交流讨论,可能想到用全等三角形知识或等腰三角形的“三线合一”性等加以证明。(两位同学演板,其余同学自主完成,然后评析完善)
师:引导学生思考分析每种证明方法的优劣,进一步优化解题思路。
设计意图:进一步巩固应用等腰三角形性质及全等三角形判定方法,鼓励学生使用多种不同方法解决问题,一题多解,发散思维,培养学生思维的创造性与求异性。
五、转化提升
师:出示如下证明题及图形,引导学生转化,尽量用不同方法证明,如图,已知在△ABC中,AB=AC,BD⊥AC于D。求证:∠BAC=2∠DBC。
生:先自主思考,再集体讨论,然后两位同学分享解题方法。
师:板书学生回答的主要内容,共同评析学生的解题方法。
设计意图:再次利用等腰三角形的“三线合一”性解决问题,或综合利用“等边对等角”及三角形内角和定理解决问题,渗透转化思想,锻炼学生思维的灵活性与可逆性。
六、畅所欲言
师:本节课的学习活动即将结束,谈谈你的感想与收获吧!
生:梳理思路,畅谈本节课学习收获与感受,学会分享。
设计意图:引导学生梳理思路,从整体上建构本节课所学知识,反思自己的学习过程,发展有序思考及有条理地与表达能力。
七、作业布置
师:出示如下作业:1.教科书第136页第3、第4题;2.完成本课时《同步练习》。
生:记录,准备课余时间完成。
设计意图:进一步巩固本节课所学知识内容,将知识巩固与能力培养延伸到课外。
