沪科版八年级上册数学 15.4.1角平分线及其画法 教案
文档属性
| 名称 | 沪科版八年级上册数学 15.4.1角平分线及其画法 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 96.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 10:51:06 | ||
图片预览

文档简介
15.4角的平分线
--------角平分线的画法
教学目标
会用尺规作已知角的平分线
会用尺规过一点作已知直线的垂线
教学重点:用尺规作角的平分线
教学难点:尺规作图方法的探究,作法的正确性的证明
教学准备:学生学案、圆规、直尺、多媒体课件
教学设计
一、复习引入
我们已经学习了怎样作出线段的垂直平分线,还记得是哪些方法吗?我们今天来研究角的平分线的作法. 提出问题1
问题1已知∠AOB,你有哪些办法可以画出它的平分线?动手试一试,和小伙伴分享.
引导学生尝试折纸法和度量法.那么我们是否也能用尺规的办法来作出角的平分线呢?
问题2 什么是尺规作图?
尺规作图: 利用没有刻度的直尺和圆规来画图的方法
二、课堂探究
1、如何用尺规作出一个角的平分线呢?
已知:∠AOB
求作:∠AOB的平分线OP
避免简单的技能的模仿,通过一些问题引导学生开动脑筋,自己筹划解决问题的办法,
问题1∠AOB的平分线是什么图形?
问题2怎么确定一条射线?
问题3这条射线有什么特别的性质?
问题4 根据我们的经验,在怎样的条件下会出现两个相等的角?
学生独立思考,讨论怎样创造条件把∠AOB分成两个相等的角:∠AOP和∠BOP,教师指导学生小组讨论并根据讨论尝试尺规画图并最终锁定方法,并写出作法
作法:
(1)以O为圆心,任意长为半径画弧分别交OA、OB于点M、N;
(2)分别以点M、N为圆心,以大于长为半径在角的内部画弧交于点P;
(3)作射线OP,则OP为所要求作的∠AOB的平分线.
注意: (1) “以大于长为半径”的原因;
(2)保留作图痕迹;
(3)结论的合理性的证明.
三、问题解决:
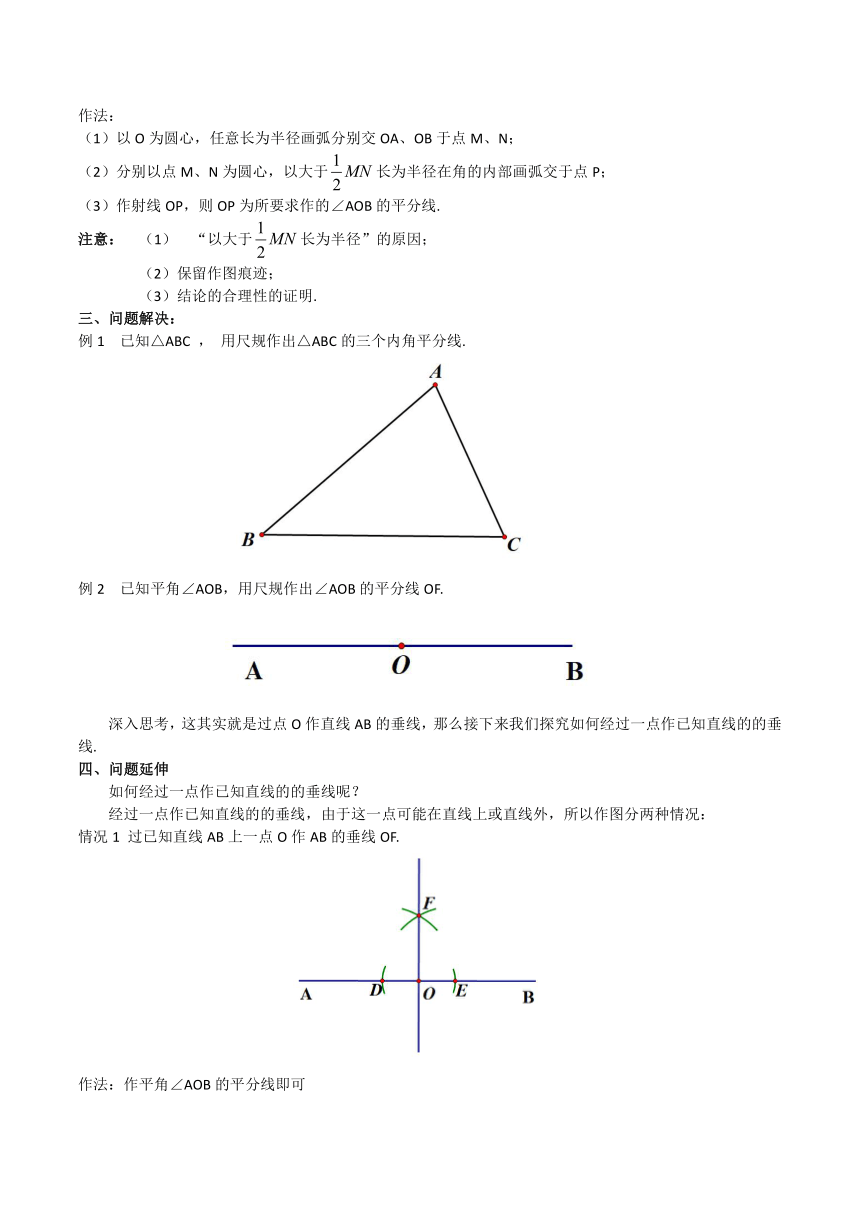
例1 已知△ABC , 用尺规作出△ABC的三个内角平分线.
例2 已知平角∠AOB,用尺规作出∠AOB的平分线OF.
深入思考,这其实就是过点O作直线AB的垂线,那么接下来我们探究如何经过一点作已知直线的的垂线.
四、问题延伸
如何经过一点作已知直线的的垂线呢?
经过一点作已知直线的的垂线,由于这一点可能在直线上或直线外,所以作图分两种情况:
情况1 过已知直线AB上一点O作AB的垂线OF.
作法:作平角∠AOB的平分线即可
情况2 过已知直线AB外一点O作AB的垂线OC
通过问题引导学生自己筹划解决问题的办法
问题1 我们尺规作图可以与垂线相关的线吗?
问题2可否将要作的垂线OC转化为某个线段DE的中垂线?
问题3 点O在线段DE的中垂线上,O需要满足的条件是什么?
学生独立思考,讨论怎样创造线段DE,并使点O在线段DE的中垂线上,教师指导学生小组讨论并根据讨论尝试尺规画图并最终锁定方法,并写出作法.
作法:
(1)以O为圆心,适当的长为半径画弧与直线AB交于点D、E;
(2)分别以点D、E为圆心,以大于长为半径画弧,两弧交于点C;
(3)作射线OC.
则直线OC就是所要求作的垂线.
注意: (1)适当的半径指什么?为什么?对比课本作法描述体会;
(2)保留作图痕迹;
(3)结论的合理性的证明.
五、练习提升
利用尺规作图完成下面的作图(不写作法,保留作图痕迹)
(1)把∠AOB四等分;
(2)已知线段AB,作直线BC垂直AB;
六、课堂小结
我们学会了什么?
在解决问题时,我们积极的思考,大胆的尝试,最终成功解决了问题。我们还用到了类比和转化两种数学思想 。
七、课后思索
已知:线段m,n
求作(1)等腰三角形,使其底边长为m,底边上的高为n;
(2)直角三角形,使其一直角边长为m,斜边长为n;
8、板书设计
15.4角的平分线第一课时尺规作图作已知角的平分线已知:∠AOB求作:∠AOB的平分线OP作法:(1)以O为圆心,任意长为半径画弧分别交OA、OB于点M、N;(2)分别以点M、N为圆心,以大于长为半径在角的内部画弧交于点P;(3)作射线OP,则OP为所要求作的∠AOB的平分线. 二、经过一点作已知直线的垂线情况1 过已知直线AB上一点O作AB的垂线OF. 作法:作平角∠AOB的平分线即可情况2 过已知直线AB外一点O作AB的垂线OC 作法:(1)以O为圆心,适当的长为半径画弧与直线AB交于点D、E;(2)分别以点D、E为圆心,以大于长为半径画弧,两弧交于点C;(3)作射线OC.则直线OC就是所要求作的垂线.
9、知识链接
在公元前465年左右,希腊的天文学家数学家,伊诺皮迪斯明确提出了只能用直尺和圆规来作图,他给出了两个著名的命题:由给定直线外一点做已知直线的垂线和做一个角等于已知角。后来尺规作图逐渐成为一种公约,最后总结在《几何原本》之中。
尺规作图里面有一个著名的问题,就是用尺规作正多边形,在作正七边形正九边形时,都遇到了很大的困难。后来伟大的数学家高斯在大学二年级时给出了正十七边形的尺规作图法,并且给出了哪些正多边形可以用尺规作图,解决了2000年来悬而未决的难题。
尺规作图是一个古老又年轻的话题,同样也是魅力无穷的,它是一种逆向思维的重要训练形式,也可以加深对几何知识的理解。数学就是这样奇妙又美丽,等你来挑战!
--------角平分线的画法
教学目标
会用尺规作已知角的平分线
会用尺规过一点作已知直线的垂线
教学重点:用尺规作角的平分线
教学难点:尺规作图方法的探究,作法的正确性的证明
教学准备:学生学案、圆规、直尺、多媒体课件
教学设计
一、复习引入
我们已经学习了怎样作出线段的垂直平分线,还记得是哪些方法吗?我们今天来研究角的平分线的作法. 提出问题1
问题1已知∠AOB,你有哪些办法可以画出它的平分线?动手试一试,和小伙伴分享.
引导学生尝试折纸法和度量法.那么我们是否也能用尺规的办法来作出角的平分线呢?
问题2 什么是尺规作图?
尺规作图: 利用没有刻度的直尺和圆规来画图的方法
二、课堂探究
1、如何用尺规作出一个角的平分线呢?
已知:∠AOB
求作:∠AOB的平分线OP
避免简单的技能的模仿,通过一些问题引导学生开动脑筋,自己筹划解决问题的办法,
问题1∠AOB的平分线是什么图形?
问题2怎么确定一条射线?
问题3这条射线有什么特别的性质?
问题4 根据我们的经验,在怎样的条件下会出现两个相等的角?
学生独立思考,讨论怎样创造条件把∠AOB分成两个相等的角:∠AOP和∠BOP,教师指导学生小组讨论并根据讨论尝试尺规画图并最终锁定方法,并写出作法
作法:
(1)以O为圆心,任意长为半径画弧分别交OA、OB于点M、N;
(2)分别以点M、N为圆心,以大于长为半径在角的内部画弧交于点P;
(3)作射线OP,则OP为所要求作的∠AOB的平分线.
注意: (1) “以大于长为半径”的原因;
(2)保留作图痕迹;
(3)结论的合理性的证明.
三、问题解决:
例1 已知△ABC , 用尺规作出△ABC的三个内角平分线.
例2 已知平角∠AOB,用尺规作出∠AOB的平分线OF.
深入思考,这其实就是过点O作直线AB的垂线,那么接下来我们探究如何经过一点作已知直线的的垂线.
四、问题延伸
如何经过一点作已知直线的的垂线呢?
经过一点作已知直线的的垂线,由于这一点可能在直线上或直线外,所以作图分两种情况:
情况1 过已知直线AB上一点O作AB的垂线OF.
作法:作平角∠AOB的平分线即可
情况2 过已知直线AB外一点O作AB的垂线OC
通过问题引导学生自己筹划解决问题的办法
问题1 我们尺规作图可以与垂线相关的线吗?
问题2可否将要作的垂线OC转化为某个线段DE的中垂线?
问题3 点O在线段DE的中垂线上,O需要满足的条件是什么?
学生独立思考,讨论怎样创造线段DE,并使点O在线段DE的中垂线上,教师指导学生小组讨论并根据讨论尝试尺规画图并最终锁定方法,并写出作法.
作法:
(1)以O为圆心,适当的长为半径画弧与直线AB交于点D、E;
(2)分别以点D、E为圆心,以大于长为半径画弧,两弧交于点C;
(3)作射线OC.
则直线OC就是所要求作的垂线.
注意: (1)适当的半径指什么?为什么?对比课本作法描述体会;
(2)保留作图痕迹;
(3)结论的合理性的证明.
五、练习提升
利用尺规作图完成下面的作图(不写作法,保留作图痕迹)
(1)把∠AOB四等分;
(2)已知线段AB,作直线BC垂直AB;
六、课堂小结
我们学会了什么?
在解决问题时,我们积极的思考,大胆的尝试,最终成功解决了问题。我们还用到了类比和转化两种数学思想 。
七、课后思索
已知:线段m,n
求作(1)等腰三角形,使其底边长为m,底边上的高为n;
(2)直角三角形,使其一直角边长为m,斜边长为n;
8、板书设计
15.4角的平分线第一课时尺规作图作已知角的平分线已知:∠AOB求作:∠AOB的平分线OP作法:(1)以O为圆心,任意长为半径画弧分别交OA、OB于点M、N;(2)分别以点M、N为圆心,以大于长为半径在角的内部画弧交于点P;(3)作射线OP,则OP为所要求作的∠AOB的平分线. 二、经过一点作已知直线的垂线情况1 过已知直线AB上一点O作AB的垂线OF. 作法:作平角∠AOB的平分线即可情况2 过已知直线AB外一点O作AB的垂线OC 作法:(1)以O为圆心,适当的长为半径画弧与直线AB交于点D、E;(2)分别以点D、E为圆心,以大于长为半径画弧,两弧交于点C;(3)作射线OC.则直线OC就是所要求作的垂线.
9、知识链接
在公元前465年左右,希腊的天文学家数学家,伊诺皮迪斯明确提出了只能用直尺和圆规来作图,他给出了两个著名的命题:由给定直线外一点做已知直线的垂线和做一个角等于已知角。后来尺规作图逐渐成为一种公约,最后总结在《几何原本》之中。
尺规作图里面有一个著名的问题,就是用尺规作正多边形,在作正七边形正九边形时,都遇到了很大的困难。后来伟大的数学家高斯在大学二年级时给出了正十七边形的尺规作图法,并且给出了哪些正多边形可以用尺规作图,解决了2000年来悬而未决的难题。
尺规作图是一个古老又年轻的话题,同样也是魅力无穷的,它是一种逆向思维的重要训练形式,也可以加深对几何知识的理解。数学就是这样奇妙又美丽,等你来挑战!
