沪科版八年级上册数学 15.4.2角平分线的性质定理 教案
文档属性
| 名称 | 沪科版八年级上册数学 15.4.2角平分线的性质定理 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 94.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 10:51:44 | ||
图片预览

文档简介
15.4 角的平分线
一、教学目标
1.使学生掌握角平分线定理及其逆定理,培养学生探索知识的能力。
2.使学生了解能利用角平分线定理及其逆定理证明角或线段相等。
3.渗透点的集合的数学思想。从事物特殊性入手,总结归纳事物的一般性。体现在研究问题时注意纯粹性与完备性,准确、全面地思考问题。
二、教学重点和难点
1.重点:(1)角平分线的性质和判定。(2)点到角的边的距离要强调垂直关系。
2.难点:(1)分清文字命题中的题设(已知)和结论,掌握证明题格式。
(2)把角平分线看作点的集合。
三、教学方法
引导学生发现、探索、研究问题,归纳结论的方法。
四、教学手段
利用投影仪、教具(等腰三角形纸片)使教学反馈速度快、直观。
五、教学过程
(一)复习提问
1.角平分线的概念,角平分线与三角形的角平分线的区别和联系。
2.点到直线(或射线)距离的意义。
(二)引入新课
第一节课已经介绍过角的平分线的概念,那么它有什么重要性质呢?怎样找到这个角的平分线?同学们首先看(教具)。
(1)有一张剪好的纸片,怎样找这个角的平分线?(引导学生回答)。
(2)大家知道,只要把纸片对折,使角的两边叠合在一起,把纸片展开后的折痕就是这个角的平分线,如图3-48。如果我们把对折的纸片继续折一次,然后把纸片展开,就会出现两条折痕,如图3-49中的PM和PN,不难发现,这两条折痕的长相等,而且这种等长的折痕我们可以找出无数对。由此可见,角的平分线除了有平分角的性质,还有其它的性质,这节我们就来研究这个问题。
(三)讲解新课
定理1 在角的平分线上的点到这个角的两边的距离相等。
要向学生讲明,证明这个定理,首先要分清题设和结论,既为写已知、求证做准备,又为引入逆命题及讨论原、逆命题的关系打基础,然后把条件和结论具体化,符号化,写出已知、求证和证明。
题设:一个点在一个角的平分线上。
结论:它到角的两边的距离相等。
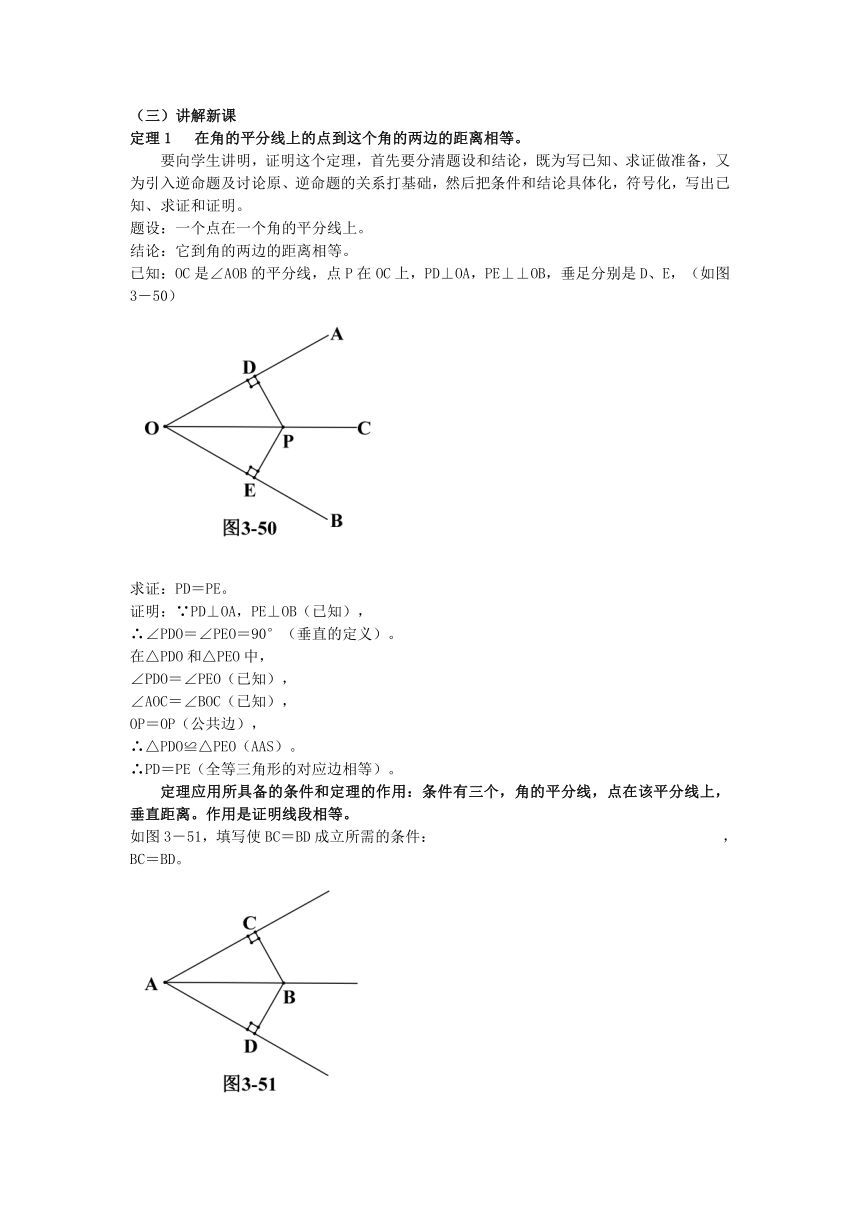
已知:OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥⊥OB,垂足分别是D、E,(如图3-50)
求证:PD=PE。
证明:∵PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°(垂直的定义)。
在△PDO和△PEO中,
∠PDO=∠PEO(已知),
∠AOC=∠BOC(已知),
OP=OP(公共边),
∴△PDO≌△PEO(AAS)。
∴PD=PE(全等三角形的对应边相等)。
定理应用所具备的条件和定理的作用:条件有三个,角的平分线,点在该平分线上,垂直距离。作用是证明线段相等。
如图3-51,填写使BC=BD成立所需的条件: , BC=BD。
猜想图3-51中,由BC⊥AC于点C,BD⊥AD于点D,BC=BD,可以得到什么结论?
用文字语言概括上述猜想,并说明这个命题与定理1有什么联系与区别?
定理2 到一个角的两边的距离相等的点,在这个角的平分线上。
引导学生分析条件、结论,画出图形,写出已知、求证和证明。
已知:PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE,如图3-52。
求证:点P在∠AOB的平分线上。
证明:经过点P作射线OC。
∵PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°(垂直定义)。
在Rt△PDO和Rt△PEO中,
OP=OP(公共边),
PD=PE(已知),
∴Rt△PDO≌Rt△PEO(HL)。
∴∠AOC=∠BOC(全等三角形的对应角相等)。
∴OC是∠AOB 的平分线。
想一想:
在一个角的内部,除角平分线上的点以外,还能找到“到角的两边距离相等”的点吗?
并说明为什么?
在角平分线上,是否有“到角的两边距离不相等的点”呢?为什么?
由定理1、2可知,在一个角内,到角的两边距离相等的点,都在这个角的平分线上;反过来,角的平分线上的点到角的两边距离相等。于是得到下面的结论:
角的平分线是到角的两边距离相等的所有点的集合。
此结论为以后研究轨迹打下基础。
例:已知:如图3-53,四边形ABCD中,AB⊥BC,AD⊥DC,B、D为垂足,线段AC平分∠C,求证:BC=DC。
分析:要证BC=DC,须证点C在∠A平分线上,
须证∠1=∠2,即证90°-∠3=90°-∠4,这由已知条件线段AC平分∠C便可得证。
(例题讲解利用投影仪PPT展示)
(四)课堂小结:
(1)定理1是角平分线的性质定理,只要证出一射线是某角的平分线,就可知道它上面的点到角的两边距离相等,利用它可以证明线段相等;定理2是角平分线的判定定理,只要证出一个点到角的两边距离相等,就可以判定该点与顶点联线是这个角的平分线,利用它可以证明角相等。
(2)用这两个定理,一定具备两个垂直距离(即点到直线的距离)。证明过程中要直接应用这两个定理,而不要去寻找全等三角形(这样作实际是重新证了一次定理)。
一、教学目标
1.使学生掌握角平分线定理及其逆定理,培养学生探索知识的能力。
2.使学生了解能利用角平分线定理及其逆定理证明角或线段相等。
3.渗透点的集合的数学思想。从事物特殊性入手,总结归纳事物的一般性。体现在研究问题时注意纯粹性与完备性,准确、全面地思考问题。
二、教学重点和难点
1.重点:(1)角平分线的性质和判定。(2)点到角的边的距离要强调垂直关系。
2.难点:(1)分清文字命题中的题设(已知)和结论,掌握证明题格式。
(2)把角平分线看作点的集合。
三、教学方法
引导学生发现、探索、研究问题,归纳结论的方法。
四、教学手段
利用投影仪、教具(等腰三角形纸片)使教学反馈速度快、直观。
五、教学过程
(一)复习提问
1.角平分线的概念,角平分线与三角形的角平分线的区别和联系。
2.点到直线(或射线)距离的意义。
(二)引入新课
第一节课已经介绍过角的平分线的概念,那么它有什么重要性质呢?怎样找到这个角的平分线?同学们首先看(教具)。
(1)有一张剪好的纸片,怎样找这个角的平分线?(引导学生回答)。
(2)大家知道,只要把纸片对折,使角的两边叠合在一起,把纸片展开后的折痕就是这个角的平分线,如图3-48。如果我们把对折的纸片继续折一次,然后把纸片展开,就会出现两条折痕,如图3-49中的PM和PN,不难发现,这两条折痕的长相等,而且这种等长的折痕我们可以找出无数对。由此可见,角的平分线除了有平分角的性质,还有其它的性质,这节我们就来研究这个问题。
(三)讲解新课
定理1 在角的平分线上的点到这个角的两边的距离相等。
要向学生讲明,证明这个定理,首先要分清题设和结论,既为写已知、求证做准备,又为引入逆命题及讨论原、逆命题的关系打基础,然后把条件和结论具体化,符号化,写出已知、求证和证明。
题设:一个点在一个角的平分线上。
结论:它到角的两边的距离相等。
已知:OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥⊥OB,垂足分别是D、E,(如图3-50)
求证:PD=PE。
证明:∵PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°(垂直的定义)。
在△PDO和△PEO中,
∠PDO=∠PEO(已知),
∠AOC=∠BOC(已知),
OP=OP(公共边),
∴△PDO≌△PEO(AAS)。
∴PD=PE(全等三角形的对应边相等)。
定理应用所具备的条件和定理的作用:条件有三个,角的平分线,点在该平分线上,垂直距离。作用是证明线段相等。
如图3-51,填写使BC=BD成立所需的条件: , BC=BD。
猜想图3-51中,由BC⊥AC于点C,BD⊥AD于点D,BC=BD,可以得到什么结论?
用文字语言概括上述猜想,并说明这个命题与定理1有什么联系与区别?
定理2 到一个角的两边的距离相等的点,在这个角的平分线上。
引导学生分析条件、结论,画出图形,写出已知、求证和证明。
已知:PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE,如图3-52。
求证:点P在∠AOB的平分线上。
证明:经过点P作射线OC。
∵PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°(垂直定义)。
在Rt△PDO和Rt△PEO中,
OP=OP(公共边),
PD=PE(已知),
∴Rt△PDO≌Rt△PEO(HL)。
∴∠AOC=∠BOC(全等三角形的对应角相等)。
∴OC是∠AOB 的平分线。
想一想:
在一个角的内部,除角平分线上的点以外,还能找到“到角的两边距离相等”的点吗?
并说明为什么?
在角平分线上,是否有“到角的两边距离不相等的点”呢?为什么?
由定理1、2可知,在一个角内,到角的两边距离相等的点,都在这个角的平分线上;反过来,角的平分线上的点到角的两边距离相等。于是得到下面的结论:
角的平分线是到角的两边距离相等的所有点的集合。
此结论为以后研究轨迹打下基础。
例:已知:如图3-53,四边形ABCD中,AB⊥BC,AD⊥DC,B、D为垂足,线段AC平分∠C,求证:BC=DC。
分析:要证BC=DC,须证点C在∠A平分线上,
须证∠1=∠2,即证90°-∠3=90°-∠4,这由已知条件线段AC平分∠C便可得证。
(例题讲解利用投影仪PPT展示)
(四)课堂小结:
(1)定理1是角平分线的性质定理,只要证出一射线是某角的平分线,就可知道它上面的点到角的两边距离相等,利用它可以证明线段相等;定理2是角平分线的判定定理,只要证出一个点到角的两边距离相等,就可以判定该点与顶点联线是这个角的平分线,利用它可以证明角相等。
(2)用这两个定理,一定具备两个垂直距离(即点到直线的距离)。证明过程中要直接应用这两个定理,而不要去寻找全等三角形(这样作实际是重新证了一次定理)。
