江西省吉安市第一中学2022-2023学年高三上学期期中考试文科数学试题(Word版含答案)
文档属性
| 名称 | 江西省吉安市第一中学2022-2023学年高三上学期期中考试文科数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 11:11:00 | ||
图片预览

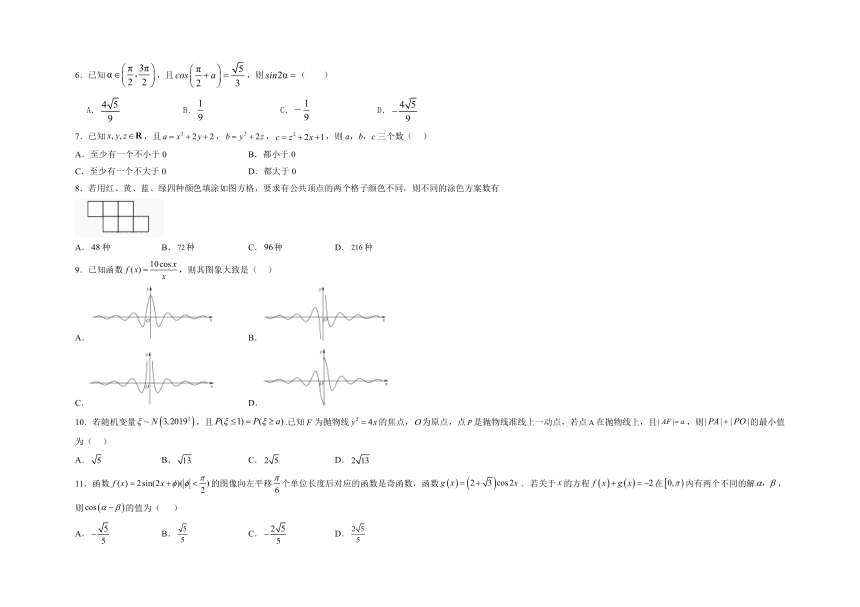



文档简介
吉安市名校2022-2023学年高三上学期期中考试
数学试卷(文科)
一、选择题(本大题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.设集合,,则( )
A. B. C. D.
2.某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该校共有2000名同学,每名同学依据自己的兴趣爱好最多可参加其中一个,各个社团的人数比例的饼状图如图所示,其中参加朗诵社团的同学有8名,参加太极拳社团的有12名,则( )
A.这五个社团的总人数为100
B.脱口秀社团的人数占五个社团总人数的20%
C.这五个社团总人数占该校学生人数的8%
D.从这五个社团中任选一人,其来脱口秀社团或舞蹈社团的概率为50%
3.已知是等比数列,若,且,则( )
A. B. C. D.
4.的展开式中的系数为( )
A.25 B.20 C.15 D.10
5.已知在区间上单调递增,则实数的取值范围是( )
A. B. C. D.
6.已知,且,则( )
A. B. C.- D.
7.已知,且,,,则a,b,c三个数( )
A.至少有一个不小于0 B.都小于0
C.至少有一个不大于0 D.都大于0
8.若用红、黄、蓝、绿四种颜色填涂如图方格,要求有公共顶点的两个格子颜色不同,则不同的涂色方案数有
A.种 B.种 C.种 D.种
9.已知函数,则其图象大致是( )
A. B.
C. D.
10.若随机变量,且.已知为抛物线的焦点,为原点,点是抛物线准线上一动点,若点在抛物线上,且,则的最小值为( )
A. B. C. D.
11.函数的图像向左平移个单位长度后对应的函数是奇函数,函数.若关于的方程在内有两个不同的解,则的值为( )
A. B. C. D.
12.将方程 的实数根称为函数 的“新驻点”.记函数 , 的“新驻点”分别为a,b,c,则( )
A. B. C. D.
二、填空题(本大题共4个小题,每小题5分,共20分。)
13.某人有3种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点上各装一个灯泡,要求同一条线段两端的灯泡不同色,则不同的安装方法共有____________种.(用数字作答)
14.已知平面向量,,,,满足,,,若,则的取值范围是________.
15.如图所示,已知双曲线:的右焦点为,双曲线的右支上一点,它关于原点的对称点为,满足,且,则双曲线的离心率是 .
16.如图,在单位正方体中,点P是线段上的动点,给出以下四个命题:
①直线与直线所成角的大小为定值;
②二面角的大小为定值;
③若Q是对角线,上一点,则长度的最小值为;
④若R是线段BD上一动点,则直线PR与直线有可能平行.
其中真命题有 (填序号).
三、解答题(本大题共6小题,共70分。解答应写出必要的文字说明或推理、验算过程。)
17.(本题12分)记的内角的对边分别为,已知.
(1)求的值;
(2)若的外接圆半径为,求的面积.
18.(本题12分)如图, 四棱锥中,底面为矩形,平面, 点在线段上.
(1)若为的中点, 证明:平面;
(2)若,,若二面角的大小为,试求的值.
19.(本题12分) 某地区对高一年级学生进行体质健康测试(简称体测),现随机抽取了900名学生的体测结果等级(“良好及以下”或“优秀”)进行分析.得到如下列联表:
良好及以下 优秀 合计
男 450 200 650
女 150 100 250
合计 600 300 900
附表及公式:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
其中,.
(1)计算并判断是否有99%的把握认为本次体测结果等级与性别有关系?
(2)将频率视为概率,用样本估计总体.若从该地区高一所有学生中,采取随机抽样的方法每次抽取1名学生成绩进行具体指标分析,连续抽取3次,且各次抽取的结果相互独立,记被抽取到的3名学生的体测等级为“优秀”的人数为,求的分布列和数学期望.
20.(本题12分)已知椭圆的一个焦点与短轴的一个端点连线的倾斜角为,直线与椭圆相交于和两点,且为坐标原点.
(1)求椭圆的方程;
(2)直线与椭圆交于两点,直线的斜率为,直线的斜率为,且,求的取值范围.
21.(本题12分) 已知指数函数若函数,且满足:
(1)求指数函数的解析式;
(2)已知函数 ,若有两个不同的实根,求实数的取值范围.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分
22.(本题10分)选修4—4:坐标系与参数方程
已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
23.(本题10分) 选修4—5:不等式选讲
已知函数.
(1)求不等式的解集;
(2)若,且,其中是的最小值,求的最小值.
答案
1.D
【分析】利用交集运算即可.
【详解】因为,,所以
故选:D
2.B
【分析】根据饼状图及有关数据得各个社团比例,计算人数及相应概率判断各选项.
【详解】这五个社团的总人数为,.A错误,C错误.
因为太极拳社团人数的占比为,所以脱口秀社团人数的占比为
,B正确.从这五个社团中任选一人,其来自脱口秀社团或舞蹈社团的概率为,D错误.
故选:B.
3.C
【分析】分别求出和展开式中的系数,最后相加即可.
【详解】由题意,.
故答案为:C.
4.B
【分析】根据二项式系数的增减性即可求解.
【详解】的展开式中第5项的二项式系数为,要使最大,由二项式系数的单调性可知当时,最大,故,
故选:B.
5.D
【分析】由题意可知在上恒成立,即在上恒成立,参变分离,构造函数,求出的最小值即可.
【详解】因为,所以,
因为在区间上单调递增,所以在上恒成立,
即在上恒成立,所以,令,则,当时,所以在上单调递增,又因为,且,所以,
故选:D.
6.A
【分析】根据三角函数的诱导公式和基本关系式,求得,,结合正弦的倍角公式,即可求解.
【详解】由已知得,又因为,故
故答案为:A
7.A
【分析】由配方可得,从而得出答案.
【详解】
所以,则a,b,c三个数至少有一个不小于0
故选:A
8.C
【详解】分析:直接按照乘法分步原理解答.
详解:
按照以下顺序涂色,
,
所以由乘法分步原理得总的方案数为种.
所以总的方案数为96,
故答案为:C
点睛:(1)本题主要考查排列组合计数原理的应用,意在考查学生的逻辑思维能力和排列组合的基本运算能力.解答排列组合时,要思路清晰,排组分清.(2)解答本题时,要注意审题,“有公共顶点的两个格子颜色不同”,如C和D有公共的顶点,所以颜色不能相同.
9.B
【分析】利用排除法,先判断函数的奇偶性,再根据函数值的变化情况分析判断.
【详解】函数的定义域为,
因为,
所以为奇函数,其图象关于原点对称,所以排除AC,
当时,当时,,,
所以,所以排除D,
故选:B
10.D
【分析】根据已知条件先得到的值即得到了的值,再利用抛物线的定义由的值可得到点的坐标为,要求的最小值即要在准线上找一点到两个定点的距离之和最小,最后利用平面几何的方法即可求出距离之和的最小值.
【详解】随机变量,且,
1和关于对称,
即,
设为第一象限中的点,,
抛物线方程为:,,
解得即,
关于准线的对称点为,
根据对称性可得:
当且仅当三点共线时等号成立.如图
故选:D
【点睛】本题考查了利用抛物线的定义求解距离,定直线上的动点到两个定点的距离之和的最小值,关键是利用对称性把距离之和最小值转化为三点共线问题,属于较难题.
11.D
【分析】利用函数的图象变换规律,利用三角函数的图象和三角恒等变形,可得,即,,从而得到,进而得到的值.
【详解】函数的图像向左平移个单位长度后,可得的图象.
由条件为奇函数,则,即
又,所以,即
关于的方程在内有两个不同的解,
即在内有两个不同的解,
即在内有两个不同的解,
即,其中(为锐角) 在内有两个不同的解,
即方程即在内有两个不同的解,
由,则,
所以,
所以
则,即,
所以,
故选:D
【点睛】本题主要考查函数的图象变换规律,三角函数的图象的对称性,诱导公式,正弦函数的定义域和值域,属于中档题.
12.A
【分析】根据新定义,利用指数式求得a;利用对数式,结合利用导数研究函数的单调性求得b;根据三角函数的性质求得c,从而求解
【详解】解:由f(x)=ex-x得f'(x)=ex-1,则由“新驻点”的定义得f(a)=f'(a),即ea-a=ea-1,解得a=1;
由g(x)=lnx得,同理可得g(x)=g'(x),即,
构造函数,则,
当x∈(0,+∞)时,r'(x)>0,r(x)单调递增,
∵r(1)=ln1-1=-1<0,,r(b)=0,
∴1由h(x)=sinx, 得h'(x)=cosx,则sinc=cosc,所以tanc=1,∴
所以c故答案为:A
13.
【分析】利用分步计数原理,先安排底面三个顶点,再安排底面的三个顶点.由分步计数原理可知所有的安排方法.
【详解】先安排下底面三个顶点共有种不同的安排方法,
再安排上底面的三个顶点共有种不同的安排方法,
由分步计数原理可知:共有种不同的安排方法,
故答案为:.
14.
【分析】根据已知得到与终点的轨迹,设出利用圆的相关知识即可求得的范围.
【详解】由已知,,,设
不妨设,,
可得
又因为,故
所以,即
所以,易知,终点在以为圆心,为半径的圆上.
终点在以为圆心,为半径的圆上.
的取值范围为与终点距离的取值范围
故
故答案为:
15.
【分析】设双曲线的左焦点为 ,连接 , ,根据双曲线的对称性可知四边形 为平行四边形,由题意以及双曲线定义和余弦定理,进而得出 ,再利用双曲线的离心率公式变形得出双曲线 的离心率。
【详解】设双曲线的左焦点为 ,连接 , ,根据双曲线的对称性可知,
四边形 为平行四边形,由题意以及双曲线定义,
可得 ,
则 , , ,
所以 ,
即 ,即 ,
所以双曲线 的离心率为: 。
故答案为: 。
16.①②④
【分析】对于①,由正方体的性质可得,进行判断;对于②,由平面与平面所成的二面角为定值进行判断;对于③,将平面沿直线翻折到平面内,过C点做,,,此时的值最小,从而可求得结果;对于④,设,结合余弦定理可得在上必然存在一点E,使得二面角为, 设平面EBD与平面的交线为ED,则,过P点作BD的垂线PR,从而可得结论.
【详解】解:对于①,由正方体的性质可知,平面,又平面,
故,异面直线与直线的所成的角为定值,①正确;
对于②,平面即为平面,平面与平面所成的二面角为定值,
而这两个平面位置固定不变,故二面角为定值,②正确;
对于③,将平面沿直线翻折到平面内,平面图如下,
过C点做,,,
此时,的值最小,
由题可知,,
,
则,
故,又,
故的最小值为,故③错误;
对于④,在正方体中易证平面,
设,则即为二面角的平面角,
又正方体棱长为1,故,则,
由余弦定理得,故,同理,
故在上必然存在一点E,使得二面角为,
即平面平面,平面EBD与平面的交线为ED,
则,过P点作BD的垂线PR,此时平面,
又平面,故,故④正确.
故答案为:①②④.
17.(1)
(2)
【分析】(1)由正弦定理得,再由余弦定理得,代入可求;
(2)利用正弦定理得到,再依次求出的值,最后利用三角形面积公式求得结果.
(1)
在中,由正弦定理及已知,得.
又,由余弦定理得
所以.
(2)
在中,由正弦定理得,
则,
由(1)得,
,
所以.
18.(1)证明见解析
(2)
【分析】(1)连接交于,连接,利用中位线的性质可得出,再利用线面平行的判定定理可证得结论成立;
(2)以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,设,其中,利用空间向量法可得出关于的等式,结合的取值范围可求得的值,即可得解.
(1)
证明:连接交于,连接,
因为四边形为矩形,为的中点,
又因为为的中点,则,
因为平面,平面,因此,平面.
(2)
解:由题设平面,四边形为矩形,
以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
平面,平面,,
所以,,
则、、、,
设,其中,
则,,
设平面的法向量为,则,
取,可得,
易知平面的一个法向量为,
由题可得,
因为,解得,此时.
19.
(1)解:依题意, 的观测值 ,
故有99%的把握认为本次体测结果等级与性别有关系.
(2)解:依题意,体测结果等级为“优秀”的概率为 ,
的取值有0,1,2,3,
则 , ,
, ,
则 的分布列为:
0 1 2 3
P
所以 的数学期望 .
【分析】(1)根据公式求出K2的观测值,结合表中数据即可判断是否有99%的把握认为本次体测结果等级与性别有关系;
(2)写出随机变量的可能取值,求出相应的概率,列出分布列,求出数期望即可.
20.(1)
(2)
【分析】(1)由题意,建立关于的方程组,求解方程组即可得答案;
(2)设,若直线的斜率存在,设的方程为,联立方程组,由韦达定理及,可得,且,进而可得;当直线的斜率不存在时,易得.综上,即可得答案.
(1)
解:不妨设左焦点为,上顶点为,则,
所以,
因为直线与椭圆相交于和两点,且,
所以将点的坐标代入椭圆的方程,得,
联立方程组,解得,
所以椭圆的方程为;
(2)
解:设,
若直线的斜率存在,设的方程为,联立方程组,
消去得,则,
又,所以,且,即,则,
因为,
所以,整理得,
则,且恒成立,
所以,
又,且,
所以,即;
当直线的斜率不存在时,,又,解得,
所以
综上,的取值范围为.
21.
(1)解法1:
令,则;
由于为指数函数,故 ,
解法2:
设
(2)解:由题意知: ,即可
若,则 ,
若则
(ⅰ)当,即时
符合,不符合;
则,
(ⅱ)当,即时
不符合,
综上所述:的取值范围是
【分析】(1) 解法1:利用,令,则,再利用为指数函数得出k的值,从而得出指数函数f(x)的解析式;
解法2:
设 ,再利用以及函数的解析式和代入法,进而得出实数k的值,再利用 进而得出b的值, 从而得出指数函数f(x)的解析式。
(2) 由题意知分段函数的解析式为,再利用分类讨论的方法和方程求解方法以及不等式求解方法,进而得出实数的取值范围。
22.(1);(2).
【详解】试题分析:(1) 先根据同角三角函数关系cos2t+sin2t=1消参数得普通方程:(x-4)2+(y-5)2=25 ,再根据将普通方程化为极坐标方程:(2)将代入得得,也可利用直角坐标方程求交点,再转化为极坐标
试题解析: (1)∵C1的参数方程为
∴(x-4)2+(y-5)2=25(cos2t+sin2t)=25,
即C1的直角坐标方程为(x-4)2+(y-5)2=25,
把代入(x-4)2+(y-5)2=25,
化简得:.
(2)C2的直角坐标方程为x2+y2=2y,C1的直角坐标方程为(x-4)2+(y-5)2=25,
∴C1与C2交点的直角坐标为(1,1),(0,2).
∴C1与C2交点的极坐标为.
考点:参数方程化普通方程,直角坐标方程化极坐标方程
23.(1)
(2)最小值为
【分析】(1)分情况讨论将绝对值不等式转化为分段函数,解不等式即可;根据(2)由(1)知,再根据“1”的代换,根据基本不等式计算得解.
(1)
函数.
因为,
所以等价于,或,或,
解得,或,或
即不等式的解集为;
(2)
由(1)可知在上单调递减,在上单调递增,
故,即,则,
,
因为,所以,
当且仅当时,等号成立,
则,故的最小值为.
数学试卷(文科)
一、选择题(本大题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.设集合,,则( )
A. B. C. D.
2.某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该校共有2000名同学,每名同学依据自己的兴趣爱好最多可参加其中一个,各个社团的人数比例的饼状图如图所示,其中参加朗诵社团的同学有8名,参加太极拳社团的有12名,则( )
A.这五个社团的总人数为100
B.脱口秀社团的人数占五个社团总人数的20%
C.这五个社团总人数占该校学生人数的8%
D.从这五个社团中任选一人,其来脱口秀社团或舞蹈社团的概率为50%
3.已知是等比数列,若,且,则( )
A. B. C. D.
4.的展开式中的系数为( )
A.25 B.20 C.15 D.10
5.已知在区间上单调递增,则实数的取值范围是( )
A. B. C. D.
6.已知,且,则( )
A. B. C.- D.
7.已知,且,,,则a,b,c三个数( )
A.至少有一个不小于0 B.都小于0
C.至少有一个不大于0 D.都大于0
8.若用红、黄、蓝、绿四种颜色填涂如图方格,要求有公共顶点的两个格子颜色不同,则不同的涂色方案数有
A.种 B.种 C.种 D.种
9.已知函数,则其图象大致是( )
A. B.
C. D.
10.若随机变量,且.已知为抛物线的焦点,为原点,点是抛物线准线上一动点,若点在抛物线上,且,则的最小值为( )
A. B. C. D.
11.函数的图像向左平移个单位长度后对应的函数是奇函数,函数.若关于的方程在内有两个不同的解,则的值为( )
A. B. C. D.
12.将方程 的实数根称为函数 的“新驻点”.记函数 , 的“新驻点”分别为a,b,c,则( )
A. B. C. D.
二、填空题(本大题共4个小题,每小题5分,共20分。)
13.某人有3种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点上各装一个灯泡,要求同一条线段两端的灯泡不同色,则不同的安装方法共有____________种.(用数字作答)
14.已知平面向量,,,,满足,,,若,则的取值范围是________.
15.如图所示,已知双曲线:的右焦点为,双曲线的右支上一点,它关于原点的对称点为,满足,且,则双曲线的离心率是 .
16.如图,在单位正方体中,点P是线段上的动点,给出以下四个命题:
①直线与直线所成角的大小为定值;
②二面角的大小为定值;
③若Q是对角线,上一点,则长度的最小值为;
④若R是线段BD上一动点,则直线PR与直线有可能平行.
其中真命题有 (填序号).
三、解答题(本大题共6小题,共70分。解答应写出必要的文字说明或推理、验算过程。)
17.(本题12分)记的内角的对边分别为,已知.
(1)求的值;
(2)若的外接圆半径为,求的面积.
18.(本题12分)如图, 四棱锥中,底面为矩形,平面, 点在线段上.
(1)若为的中点, 证明:平面;
(2)若,,若二面角的大小为,试求的值.
19.(本题12分) 某地区对高一年级学生进行体质健康测试(简称体测),现随机抽取了900名学生的体测结果等级(“良好及以下”或“优秀”)进行分析.得到如下列联表:
良好及以下 优秀 合计
男 450 200 650
女 150 100 250
合计 600 300 900
附表及公式:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
其中,.
(1)计算并判断是否有99%的把握认为本次体测结果等级与性别有关系?
(2)将频率视为概率,用样本估计总体.若从该地区高一所有学生中,采取随机抽样的方法每次抽取1名学生成绩进行具体指标分析,连续抽取3次,且各次抽取的结果相互独立,记被抽取到的3名学生的体测等级为“优秀”的人数为,求的分布列和数学期望.
20.(本题12分)已知椭圆的一个焦点与短轴的一个端点连线的倾斜角为,直线与椭圆相交于和两点,且为坐标原点.
(1)求椭圆的方程;
(2)直线与椭圆交于两点,直线的斜率为,直线的斜率为,且,求的取值范围.
21.(本题12分) 已知指数函数若函数,且满足:
(1)求指数函数的解析式;
(2)已知函数 ,若有两个不同的实根,求实数的取值范围.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分
22.(本题10分)选修4—4:坐标系与参数方程
已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
23.(本题10分) 选修4—5:不等式选讲
已知函数.
(1)求不等式的解集;
(2)若,且,其中是的最小值,求的最小值.
答案
1.D
【分析】利用交集运算即可.
【详解】因为,,所以
故选:D
2.B
【分析】根据饼状图及有关数据得各个社团比例,计算人数及相应概率判断各选项.
【详解】这五个社团的总人数为,.A错误,C错误.
因为太极拳社团人数的占比为,所以脱口秀社团人数的占比为
,B正确.从这五个社团中任选一人,其来自脱口秀社团或舞蹈社团的概率为,D错误.
故选:B.
3.C
【分析】分别求出和展开式中的系数,最后相加即可.
【详解】由题意,.
故答案为:C.
4.B
【分析】根据二项式系数的增减性即可求解.
【详解】的展开式中第5项的二项式系数为,要使最大,由二项式系数的单调性可知当时,最大,故,
故选:B.
5.D
【分析】由题意可知在上恒成立,即在上恒成立,参变分离,构造函数,求出的最小值即可.
【详解】因为,所以,
因为在区间上单调递增,所以在上恒成立,
即在上恒成立,所以,令,则,当时,所以在上单调递增,又因为,且,所以,
故选:D.
6.A
【分析】根据三角函数的诱导公式和基本关系式,求得,,结合正弦的倍角公式,即可求解.
【详解】由已知得,又因为,故
故答案为:A
7.A
【分析】由配方可得,从而得出答案.
【详解】
所以,则a,b,c三个数至少有一个不小于0
故选:A
8.C
【详解】分析:直接按照乘法分步原理解答.
详解:
按照以下顺序涂色,
,
所以由乘法分步原理得总的方案数为种.
所以总的方案数为96,
故答案为:C
点睛:(1)本题主要考查排列组合计数原理的应用,意在考查学生的逻辑思维能力和排列组合的基本运算能力.解答排列组合时,要思路清晰,排组分清.(2)解答本题时,要注意审题,“有公共顶点的两个格子颜色不同”,如C和D有公共的顶点,所以颜色不能相同.
9.B
【分析】利用排除法,先判断函数的奇偶性,再根据函数值的变化情况分析判断.
【详解】函数的定义域为,
因为,
所以为奇函数,其图象关于原点对称,所以排除AC,
当时,当时,,,
所以,所以排除D,
故选:B
10.D
【分析】根据已知条件先得到的值即得到了的值,再利用抛物线的定义由的值可得到点的坐标为,要求的最小值即要在准线上找一点到两个定点的距离之和最小,最后利用平面几何的方法即可求出距离之和的最小值.
【详解】随机变量,且,
1和关于对称,
即,
设为第一象限中的点,,
抛物线方程为:,,
解得即,
关于准线的对称点为,
根据对称性可得:
当且仅当三点共线时等号成立.如图
故选:D
【点睛】本题考查了利用抛物线的定义求解距离,定直线上的动点到两个定点的距离之和的最小值,关键是利用对称性把距离之和最小值转化为三点共线问题,属于较难题.
11.D
【分析】利用函数的图象变换规律,利用三角函数的图象和三角恒等变形,可得,即,,从而得到,进而得到的值.
【详解】函数的图像向左平移个单位长度后,可得的图象.
由条件为奇函数,则,即
又,所以,即
关于的方程在内有两个不同的解,
即在内有两个不同的解,
即在内有两个不同的解,
即,其中(为锐角) 在内有两个不同的解,
即方程即在内有两个不同的解,
由,则,
所以,
所以
则,即,
所以,
故选:D
【点睛】本题主要考查函数的图象变换规律,三角函数的图象的对称性,诱导公式,正弦函数的定义域和值域,属于中档题.
12.A
【分析】根据新定义,利用指数式求得a;利用对数式,结合利用导数研究函数的单调性求得b;根据三角函数的性质求得c,从而求解
【详解】解:由f(x)=ex-x得f'(x)=ex-1,则由“新驻点”的定义得f(a)=f'(a),即ea-a=ea-1,解得a=1;
由g(x)=lnx得,同理可得g(x)=g'(x),即,
构造函数,则,
当x∈(0,+∞)时,r'(x)>0,r(x)单调递增,
∵r(1)=ln1-1=-1<0,,r(b)=0,
∴1
所以c
13.
【分析】利用分步计数原理,先安排底面三个顶点,再安排底面的三个顶点.由分步计数原理可知所有的安排方法.
【详解】先安排下底面三个顶点共有种不同的安排方法,
再安排上底面的三个顶点共有种不同的安排方法,
由分步计数原理可知:共有种不同的安排方法,
故答案为:.
14.
【分析】根据已知得到与终点的轨迹,设出利用圆的相关知识即可求得的范围.
【详解】由已知,,,设
不妨设,,
可得
又因为,故
所以,即
所以,易知,终点在以为圆心,为半径的圆上.
终点在以为圆心,为半径的圆上.
的取值范围为与终点距离的取值范围
故
故答案为:
15.
【分析】设双曲线的左焦点为 ,连接 , ,根据双曲线的对称性可知四边形 为平行四边形,由题意以及双曲线定义和余弦定理,进而得出 ,再利用双曲线的离心率公式变形得出双曲线 的离心率。
【详解】设双曲线的左焦点为 ,连接 , ,根据双曲线的对称性可知,
四边形 为平行四边形,由题意以及双曲线定义,
可得 ,
则 , , ,
所以 ,
即 ,即 ,
所以双曲线 的离心率为: 。
故答案为: 。
16.①②④
【分析】对于①,由正方体的性质可得,进行判断;对于②,由平面与平面所成的二面角为定值进行判断;对于③,将平面沿直线翻折到平面内,过C点做,,,此时的值最小,从而可求得结果;对于④,设,结合余弦定理可得在上必然存在一点E,使得二面角为, 设平面EBD与平面的交线为ED,则,过P点作BD的垂线PR,从而可得结论.
【详解】解:对于①,由正方体的性质可知,平面,又平面,
故,异面直线与直线的所成的角为定值,①正确;
对于②,平面即为平面,平面与平面所成的二面角为定值,
而这两个平面位置固定不变,故二面角为定值,②正确;
对于③,将平面沿直线翻折到平面内,平面图如下,
过C点做,,,
此时,的值最小,
由题可知,,
,
则,
故,又,
故的最小值为,故③错误;
对于④,在正方体中易证平面,
设,则即为二面角的平面角,
又正方体棱长为1,故,则,
由余弦定理得,故,同理,
故在上必然存在一点E,使得二面角为,
即平面平面,平面EBD与平面的交线为ED,
则,过P点作BD的垂线PR,此时平面,
又平面,故,故④正确.
故答案为:①②④.
17.(1)
(2)
【分析】(1)由正弦定理得,再由余弦定理得,代入可求;
(2)利用正弦定理得到,再依次求出的值,最后利用三角形面积公式求得结果.
(1)
在中,由正弦定理及已知,得.
又,由余弦定理得
所以.
(2)
在中,由正弦定理得,
则,
由(1)得,
,
所以.
18.(1)证明见解析
(2)
【分析】(1)连接交于,连接,利用中位线的性质可得出,再利用线面平行的判定定理可证得结论成立;
(2)以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,设,其中,利用空间向量法可得出关于的等式,结合的取值范围可求得的值,即可得解.
(1)
证明:连接交于,连接,
因为四边形为矩形,为的中点,
又因为为的中点,则,
因为平面,平面,因此,平面.
(2)
解:由题设平面,四边形为矩形,
以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
平面,平面,,
所以,,
则、、、,
设,其中,
则,,
设平面的法向量为,则,
取,可得,
易知平面的一个法向量为,
由题可得,
因为,解得,此时.
19.
(1)解:依题意, 的观测值 ,
故有99%的把握认为本次体测结果等级与性别有关系.
(2)解:依题意,体测结果等级为“优秀”的概率为 ,
的取值有0,1,2,3,
则 , ,
, ,
则 的分布列为:
0 1 2 3
P
所以 的数学期望 .
【分析】(1)根据公式求出K2的观测值,结合表中数据即可判断是否有99%的把握认为本次体测结果等级与性别有关系;
(2)写出随机变量的可能取值,求出相应的概率,列出分布列,求出数期望即可.
20.(1)
(2)
【分析】(1)由题意,建立关于的方程组,求解方程组即可得答案;
(2)设,若直线的斜率存在,设的方程为,联立方程组,由韦达定理及,可得,且,进而可得;当直线的斜率不存在时,易得.综上,即可得答案.
(1)
解:不妨设左焦点为,上顶点为,则,
所以,
因为直线与椭圆相交于和两点,且,
所以将点的坐标代入椭圆的方程,得,
联立方程组,解得,
所以椭圆的方程为;
(2)
解:设,
若直线的斜率存在,设的方程为,联立方程组,
消去得,则,
又,所以,且,即,则,
因为,
所以,整理得,
则,且恒成立,
所以,
又,且,
所以,即;
当直线的斜率不存在时,,又,解得,
所以
综上,的取值范围为.
21.
(1)解法1:
令,则;
由于为指数函数,故 ,
解法2:
设
(2)解:由题意知: ,即可
若,则 ,
若则
(ⅰ)当,即时
符合,不符合;
则,
(ⅱ)当,即时
不符合,
综上所述:的取值范围是
【分析】(1) 解法1:利用,令,则,再利用为指数函数得出k的值,从而得出指数函数f(x)的解析式;
解法2:
设 ,再利用以及函数的解析式和代入法,进而得出实数k的值,再利用 进而得出b的值, 从而得出指数函数f(x)的解析式。
(2) 由题意知分段函数的解析式为,再利用分类讨论的方法和方程求解方法以及不等式求解方法,进而得出实数的取值范围。
22.(1);(2).
【详解】试题分析:(1) 先根据同角三角函数关系cos2t+sin2t=1消参数得普通方程:(x-4)2+(y-5)2=25 ,再根据将普通方程化为极坐标方程:(2)将代入得得,也可利用直角坐标方程求交点,再转化为极坐标
试题解析: (1)∵C1的参数方程为
∴(x-4)2+(y-5)2=25(cos2t+sin2t)=25,
即C1的直角坐标方程为(x-4)2+(y-5)2=25,
把代入(x-4)2+(y-5)2=25,
化简得:.
(2)C2的直角坐标方程为x2+y2=2y,C1的直角坐标方程为(x-4)2+(y-5)2=25,
∴C1与C2交点的直角坐标为(1,1),(0,2).
∴C1与C2交点的极坐标为.
考点:参数方程化普通方程,直角坐标方程化极坐标方程
23.(1)
(2)最小值为
【分析】(1)分情况讨论将绝对值不等式转化为分段函数,解不等式即可;根据(2)由(1)知,再根据“1”的代换,根据基本不等式计算得解.
(1)
函数.
因为,
所以等价于,或,或,
解得,或,或
即不等式的解集为;
(2)
由(1)可知在上单调递减,在上单调递增,
故,即,则,
,
因为,所以,
当且仅当时,等号成立,
则,故的最小值为.
同课章节目录
