人教A版(2019)高中数学选择性必修第三册 6.3《二项式定理》名师课件(共48张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 6.3《二项式定理》名师课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览











文档简介
(共48张PPT)
二项式定理研究的是的展开式.
…
…
情境引入
问题1:的展开式是什么?
多项式乘法的再认识
规律: 每个括号内任取一个字母相乘构成了展开式中的每一项.
展开式有几项?每一项是怎样构成的?
情境引入
问题2:展开式中每一项是怎样构成的?
展开式有几项?
人教A版同步教材名师课件
二项式定理
学习目标
学 习 目 标 核心素养
掌握二项式定理及其展开式的通项公式 数学抽象
能熟练进行二项式的展开及求解某些指定的项 数学运算
会利用赋值法推导二项式系数的性质 逻辑推理
理解并掌握杨辉三角的性质 数学抽象
理解并掌握二项式定理的应用 逻辑推理和数学运算
学习目标
学习目标:
1.掌握二项式定理的概念、通项、 展开式;
2.掌握并会应用二项式定理.
学科核心素养:
1.经历由的展开式推导出的展开式的过程,发展学生的数学抽象核心素养.
2.结合实例,掌握用二项展开式的通项公式求展开式中的指定项的方法,发展学生的数学运算核心素养.
3.在应用二项式定理解决问题的过程中,发展学生的逻辑推理核心素养.
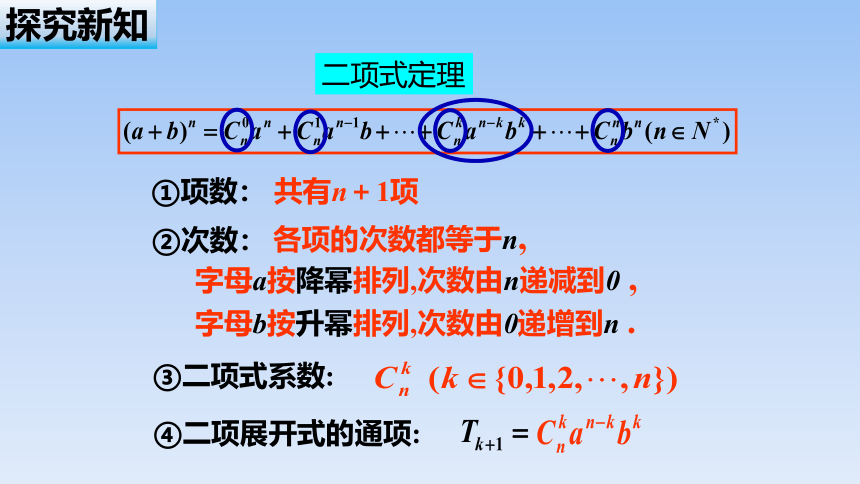
探究新知
① 项:
② 系数:
1
③ 展开式:
探究1 推导 的展开式.
探究新知
猜想
探究2 仿照上述过程,推导 的展开式.
探究新知
①项:
②系数:
探究3:请分析 的展开过程,证明猜想.
…
…
③展开式:
探究新知
④二项展开式的通项:
③二项式系数:
①项数:
②次数:
共有n+1项
各项的次数都等于n,
字母a按降幂排列,次数由n递减到0 ,
字母b按升幂排列,次数由0递增到n .
二项式定理
典例讲解
例1、求的展开式.
法一:直接展开
解析
典例讲解
例1、求的展开式.
法二:先化简后展开
解析
典例讲解
例2、求的展开式.
思考3:你能否直接求出展开式的第3项?
思考1:展开式的第3项的系数是多少?
思考2:展开式的第3项的二项式系数是多少?
典例讲解
例2、 (1)求的展开式的第4项及其二项式系数;
(2)求的展开式中项的系数.
(1) 的展开式的第4项是
其对应的二项式系数
解析
典例讲解
例2、 (1)求的展开式的第4项及其二项式系数;
(2)求的展开式中项的系数.
(2)先求出是展开式的哪一项,再求它的系数:
故项的系数.
解析
注意区别二项式系数与项的系数的概念
二项式系数: ;
项的系数:二项式系数与数字系数的积
典例讲解
例3、化简: .
公式的逆用!
解析
方法归纳
(2)二项展开式的通项:
1.二项式定理:
2.思想方法
(1)二项式系数:
(2) 用计数原理分析二项式的展开过程.
(1) 从特殊到一般的数学思维方式.
(3) 类比、等价转换的思想.
变式训练
1.求的展开式中的倒数第4项
的展开式有13项,倒数第4项是它的第10项
解析
变式训练
2.的(1)中间两项(2)常数项
解析
(1)展开式共有10项,中间两项是第5、6项
变式训练
2.的(1)中间两项(2)常数项
解析
(2)
得
探究新知
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
“杨辉三角”
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
探究新知
杨辉三角
此表在我国南宋数学家杨辉1261年所著的《详解九章算法》里就已经出现,并且北宋数学家贾宪(约公元11 世纪)已使用过它.
杨辉(南宋)
在欧洲,这个表被认为是法国数学家帕斯卡(1623-1662)首先发现的,他们把这个表叫做帕斯卡三角. 杨辉三角的发现要比欧洲早五百年左右.
探究新知
n=6----
n=5-------
n=4----------
对称性
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
n=3--------------
n=1------------------
n=2----------------
n=1------------------
n=2----------------
n=3--------------
n=1---------------------
n=2----------------
1.对称性.与首末两端“等距离”的两个二项式系数相等 .
二项式系数的性质
探究新知
4+6=10
2+1=3
例如:
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
2
1
3
4
6
10
1
7
35
21
1
35
21
7
纵向:相邻两行的数有什么关系?
在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和.(“双肩”和)
2.各二项式系数的和
二项式系数的性质
赋值法
探究新知
例4、在二项式的展开式中,求:
(1)二项式系数之和;
(2)各项系数之和;
(3)所有奇数项系数之和;
(4)系数绝对值的和.
设.
(1)二项式系数之和为.
(2)各项系数之和为,
令,
所以.
解析
典例讲解
例4、在二项式的展开式中,求:
(1)二项式系数之和;
(2)各项系数之和;
(3)所有奇数项系数之和;
(4)系数绝对值的和.
(3)由(2)知,
令,可得,
将两式相加可得.
即为所有奇数项系数之和.
解析
典例讲解
例4、在二项式的展开式中,求:
(1)二项式系数之和;
(2)各项系数之和;
(3)所有奇数项系数之和;
(4)系数绝对值的和.
(4)法一:,
令,
则 .
法二:
即为的展开式中各项系数之和,
令得,
.
解析
典例讲解
方法归纳
(1)对形如的式子求其展开式的各项系数之和,常用赋值法,只需令即可;
对的式子求其展开式各项系数之和,只需令即可.
(2)一般地,若,则展开式中各项系数之和为,奇数项系数之和为偶数项系数之和为
二项展开式中系数和的求法
变式训练
展开式的通项为
即
, 得
3. 已知
A.32 B.1 C. D.1或
解析
B
探究新知
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
当n为偶数如2、4、6时,中间一项最大
3.增减性与最大值
横向:每行系数大小变化趋势?
当n为奇数如1、3、5时,中间两项最大
n=6---
n=5------
n=4---------
n=3------------
n=1--------------------
n=2---------------
n=1--------------------
n=2---------------
n=3------------
n=1--------------------
n=2---------------
n=6---
n=5------
n=4---------
n=3------------
n=1--------------------
n=2---------------
探究新知
可知,当 时,
二项式系数前半部分逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值.
增减性与最大值
证明:(法一)
探究新知
可知,当 时,
二项式系数前半部分逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值.
证明:(法二)
增减性与最大值
探究新知
1 2 3 4 5 6
1
5
10
15
20
r
o
定义域为 { 0, 1, 2, … , n }.
其图象是7个孤立点.
函数角度
图象法
直线 作为对称轴将图象分成对称的两部分
当n= 6时,
探究新知
n
O
O
n
当n是偶数时,中间的一项 取得最大值.
当n是奇数时,中间的两项 和 相等,且同时取得最大值.
n为奇数;
如n=7
n为偶数;如n=6
4
3
3
6
7
10
20
30
20
15
6
计算各行二项式系数的和,你能发现什么规律?
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
n=6---
n=5----------
n=4--------------
n=3-------------------
n=1----------------------------
n=2-----------------------
n
探究新知
例5、在的展开式中,求:
(1)二项式系数最大的项;
(2)系数绝对值最大的项;
(3)系数最大的项.
(1)二项式系数最大的项是第11项.
(2)设系数绝对值最大的项是第项,于是
化简得,
解之得.
因为,所以,
即是系数绝对值最大的项.
典例讲解
解析
例5、在的展开式中,求:
(1)二项式系数最大的项;
(2)系数绝对值最大的项;
(3)系数最大的项.
(3)由于系数为正的项为奇数项,
故可设第项系数最大(),于是
化简得
解之得,
即第项系数最大.
典例讲解
解析
方法归纳
(1)二项式系数的最大项的求法
求二项式系数的最大项,根据二项式系数的性质对中的进行讨论.
①当为奇数时,中间两项的二项式系数最大.
②当为偶数时,中间一项的二项式系数最大.
(2)展开式中系数的最大项的求法
求展开式中系数的最大项与求二项式系数最大项是不同的,需要根据各项系数的正、负变化情况进行分析.如求
的展开式中系数的最大项,一般采用待定系数法.设展开式中各项系数分别为,且第项最大,应用, ,解出,即得出系数的最大项.
变式训练
4.求的展开式中系数最小的项.
设中第项的系数的绝对值最大,则有
,所以.
因为,
所以.
所以.
,
所以系数最小的项为.
解析
素养提炼
1.杨辉三角直观地给出了二项式系数的性质,有关杨辉三角的问题,要从横看、竖看、隔行看、连续看等多角度找出数据与组合数的关系规律.
2.求展开式中的系数或展开式中的系数的和、差的关键是给字母赋值,赋值的选择则需根据所求的展开式系数和
特征来确定.一般地对字母赋的值为1或-1,但在解决具体问题时要灵活掌握.
素养提炼
3.求展开式中系数的最大值问题.
在系数均为正的前提下,求它们的最大值只需比较相邻两个的大小,根据通项公式正确地列出不等式(组)即可.即设第项的系数最大,则的系数的系数的系数的系数.
当堂练习
1.已知展开式的二项式系数之和为256.
(1)求;
(2)若展开式中常数项为,求的值;
(3)若展开式中系数最大项只有第6项和第7项,求的取值情况.
(1)二项式系数之和为,可得.
(2)设常数项为第项,则
,
故,即,
则,解得.
解析
当堂练习
1.已知展开式的二项式系数之和为256.
(1)求;
(2)若展开式中常数项为,求的值;
(3)若展开式中系数最大项只有第6项和第7项,求的取值情况.
(3)易知,设第项系数最大.
则,
化简可得.
由于只有第6项和第7项系数最大,
所以.即.
所以只能等于2.
解析
当堂练习
2.若的展开式中只有第6项系数最大,则该展开式中的常数项为( )
A.210 B.252 C.462 D.10
由于展开式中只有第6项的系数最大,且其系数等于其二项式系数,所以展开式项数为11,从而,于是得其常数项为252.
解析
B
当堂练习
3.如何求展开式中含的项?
展开式中含的项是由中的与分别与展开式中常数项及项分别相乘再把积相加得.即展开式中含的项为.
解析
4.试证:在展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
在二项式定理中,令,则:
即在展开式中,奇数项的二项式系数的和等于
偶数项的二项式系数的和.
赋值法
解析
当堂练习
归纳小结
二项式定理
概念 公式=_________________________________称为二项式定理
二项式系数 各项系数____()叫做展开式的二项式系数
二项式通项 是展开式中的第 项,可记做
二项展开式
作 业
课本P34习题6.3:5、6
二项式定理研究的是的展开式.
…
…
情境引入
问题1:的展开式是什么?
多项式乘法的再认识
规律: 每个括号内任取一个字母相乘构成了展开式中的每一项.
展开式有几项?每一项是怎样构成的?
情境引入
问题2:展开式中每一项是怎样构成的?
展开式有几项?
人教A版同步教材名师课件
二项式定理
学习目标
学 习 目 标 核心素养
掌握二项式定理及其展开式的通项公式 数学抽象
能熟练进行二项式的展开及求解某些指定的项 数学运算
会利用赋值法推导二项式系数的性质 逻辑推理
理解并掌握杨辉三角的性质 数学抽象
理解并掌握二项式定理的应用 逻辑推理和数学运算
学习目标
学习目标:
1.掌握二项式定理的概念、通项、 展开式;
2.掌握并会应用二项式定理.
学科核心素养:
1.经历由的展开式推导出的展开式的过程,发展学生的数学抽象核心素养.
2.结合实例,掌握用二项展开式的通项公式求展开式中的指定项的方法,发展学生的数学运算核心素养.
3.在应用二项式定理解决问题的过程中,发展学生的逻辑推理核心素养.
探究新知
① 项:
② 系数:
1
③ 展开式:
探究1 推导 的展开式.
探究新知
猜想
探究2 仿照上述过程,推导 的展开式.
探究新知
①项:
②系数:
探究3:请分析 的展开过程,证明猜想.
…
…
③展开式:
探究新知
④二项展开式的通项:
③二项式系数:
①项数:
②次数:
共有n+1项
各项的次数都等于n,
字母a按降幂排列,次数由n递减到0 ,
字母b按升幂排列,次数由0递增到n .
二项式定理
典例讲解
例1、求的展开式.
法一:直接展开
解析
典例讲解
例1、求的展开式.
法二:先化简后展开
解析
典例讲解
例2、求的展开式.
思考3:你能否直接求出展开式的第3项?
思考1:展开式的第3项的系数是多少?
思考2:展开式的第3项的二项式系数是多少?
典例讲解
例2、 (1)求的展开式的第4项及其二项式系数;
(2)求的展开式中项的系数.
(1) 的展开式的第4项是
其对应的二项式系数
解析
典例讲解
例2、 (1)求的展开式的第4项及其二项式系数;
(2)求的展开式中项的系数.
(2)先求出是展开式的哪一项,再求它的系数:
故项的系数.
解析
注意区别二项式系数与项的系数的概念
二项式系数: ;
项的系数:二项式系数与数字系数的积
典例讲解
例3、化简: .
公式的逆用!
解析
方法归纳
(2)二项展开式的通项:
1.二项式定理:
2.思想方法
(1)二项式系数:
(2) 用计数原理分析二项式的展开过程.
(1) 从特殊到一般的数学思维方式.
(3) 类比、等价转换的思想.
变式训练
1.求的展开式中的倒数第4项
的展开式有13项,倒数第4项是它的第10项
解析
变式训练
2.的(1)中间两项(2)常数项
解析
(1)展开式共有10项,中间两项是第5、6项
变式训练
2.的(1)中间两项(2)常数项
解析
(2)
得
探究新知
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
“杨辉三角”
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
探究新知
杨辉三角
此表在我国南宋数学家杨辉1261年所著的《详解九章算法》里就已经出现,并且北宋数学家贾宪(约公元11 世纪)已使用过它.
杨辉(南宋)
在欧洲,这个表被认为是法国数学家帕斯卡(1623-1662)首先发现的,他们把这个表叫做帕斯卡三角. 杨辉三角的发现要比欧洲早五百年左右.
探究新知
n=6----
n=5-------
n=4----------
对称性
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
n=3--------------
n=1------------------
n=2----------------
n=1------------------
n=2----------------
n=3--------------
n=1---------------------
n=2----------------
1.对称性.与首末两端“等距离”的两个二项式系数相等 .
二项式系数的性质
探究新知
4+6=10
2+1=3
例如:
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
2
1
3
4
6
10
1
7
35
21
1
35
21
7
纵向:相邻两行的数有什么关系?
在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和.(“双肩”和)
2.各二项式系数的和
二项式系数的性质
赋值法
探究新知
例4、在二项式的展开式中,求:
(1)二项式系数之和;
(2)各项系数之和;
(3)所有奇数项系数之和;
(4)系数绝对值的和.
设.
(1)二项式系数之和为.
(2)各项系数之和为,
令,
所以.
解析
典例讲解
例4、在二项式的展开式中,求:
(1)二项式系数之和;
(2)各项系数之和;
(3)所有奇数项系数之和;
(4)系数绝对值的和.
(3)由(2)知,
令,可得,
将两式相加可得.
即为所有奇数项系数之和.
解析
典例讲解
例4、在二项式的展开式中,求:
(1)二项式系数之和;
(2)各项系数之和;
(3)所有奇数项系数之和;
(4)系数绝对值的和.
(4)法一:,
令,
则 .
法二:
即为的展开式中各项系数之和,
令得,
.
解析
典例讲解
方法归纳
(1)对形如的式子求其展开式的各项系数之和,常用赋值法,只需令即可;
对的式子求其展开式各项系数之和,只需令即可.
(2)一般地,若,则展开式中各项系数之和为,奇数项系数之和为偶数项系数之和为
二项展开式中系数和的求法
变式训练
展开式的通项为
即
, 得
3. 已知
A.32 B.1 C. D.1或
解析
B
探究新知
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
当n为偶数如2、4、6时,中间一项最大
3.增减性与最大值
横向:每行系数大小变化趋势?
当n为奇数如1、3、5时,中间两项最大
n=6---
n=5------
n=4---------
n=3------------
n=1--------------------
n=2---------------
n=1--------------------
n=2---------------
n=3------------
n=1--------------------
n=2---------------
n=6---
n=5------
n=4---------
n=3------------
n=1--------------------
n=2---------------
探究新知
可知,当 时,
二项式系数前半部分逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值.
增减性与最大值
证明:(法一)
探究新知
可知,当 时,
二项式系数前半部分逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值.
证明:(法二)
增减性与最大值
探究新知
1 2 3 4 5 6
1
5
10
15
20
r
o
定义域为 { 0, 1, 2, … , n }.
其图象是7个孤立点.
函数角度
图象法
直线 作为对称轴将图象分成对称的两部分
当n= 6时,
探究新知
n
O
O
n
当n是偶数时,中间的一项 取得最大值.
当n是奇数时,中间的两项 和 相等,且同时取得最大值.
n为奇数;
如n=7
n为偶数;如n=6
4
3
3
6
7
10
20
30
20
15
6
计算各行二项式系数的和,你能发现什么规律?
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
n=6---
n=5----------
n=4--------------
n=3-------------------
n=1----------------------------
n=2-----------------------
n
探究新知
例5、在的展开式中,求:
(1)二项式系数最大的项;
(2)系数绝对值最大的项;
(3)系数最大的项.
(1)二项式系数最大的项是第11项.
(2)设系数绝对值最大的项是第项,于是
化简得,
解之得.
因为,所以,
即是系数绝对值最大的项.
典例讲解
解析
例5、在的展开式中,求:
(1)二项式系数最大的项;
(2)系数绝对值最大的项;
(3)系数最大的项.
(3)由于系数为正的项为奇数项,
故可设第项系数最大(),于是
化简得
解之得,
即第项系数最大.
典例讲解
解析
方法归纳
(1)二项式系数的最大项的求法
求二项式系数的最大项,根据二项式系数的性质对中的进行讨论.
①当为奇数时,中间两项的二项式系数最大.
②当为偶数时,中间一项的二项式系数最大.
(2)展开式中系数的最大项的求法
求展开式中系数的最大项与求二项式系数最大项是不同的,需要根据各项系数的正、负变化情况进行分析.如求
的展开式中系数的最大项,一般采用待定系数法.设展开式中各项系数分别为,且第项最大,应用, ,解出,即得出系数的最大项.
变式训练
4.求的展开式中系数最小的项.
设中第项的系数的绝对值最大,则有
,所以.
因为,
所以.
所以.
,
所以系数最小的项为.
解析
素养提炼
1.杨辉三角直观地给出了二项式系数的性质,有关杨辉三角的问题,要从横看、竖看、隔行看、连续看等多角度找出数据与组合数的关系规律.
2.求展开式中的系数或展开式中的系数的和、差的关键是给字母赋值,赋值的选择则需根据所求的展开式系数和
特征来确定.一般地对字母赋的值为1或-1,但在解决具体问题时要灵活掌握.
素养提炼
3.求展开式中系数的最大值问题.
在系数均为正的前提下,求它们的最大值只需比较相邻两个的大小,根据通项公式正确地列出不等式(组)即可.即设第项的系数最大,则的系数的系数的系数的系数.
当堂练习
1.已知展开式的二项式系数之和为256.
(1)求;
(2)若展开式中常数项为,求的值;
(3)若展开式中系数最大项只有第6项和第7项,求的取值情况.
(1)二项式系数之和为,可得.
(2)设常数项为第项,则
,
故,即,
则,解得.
解析
当堂练习
1.已知展开式的二项式系数之和为256.
(1)求;
(2)若展开式中常数项为,求的值;
(3)若展开式中系数最大项只有第6项和第7项,求的取值情况.
(3)易知,设第项系数最大.
则,
化简可得.
由于只有第6项和第7项系数最大,
所以.即.
所以只能等于2.
解析
当堂练习
2.若的展开式中只有第6项系数最大,则该展开式中的常数项为( )
A.210 B.252 C.462 D.10
由于展开式中只有第6项的系数最大,且其系数等于其二项式系数,所以展开式项数为11,从而,于是得其常数项为252.
解析
B
当堂练习
3.如何求展开式中含的项?
展开式中含的项是由中的与分别与展开式中常数项及项分别相乘再把积相加得.即展开式中含的项为.
解析
4.试证:在展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
在二项式定理中,令,则:
即在展开式中,奇数项的二项式系数的和等于
偶数项的二项式系数的和.
赋值法
解析
当堂练习
归纳小结
二项式定理
概念 公式=_________________________________称为二项式定理
二项式系数 各项系数____()叫做展开式的二项式系数
二项式通项 是展开式中的第 项,可记做
二项展开式
作 业
课本P34习题6.3:5、6
