人教A版(2019)高中数学选择性必修第三册【整合课件】6.3.2二项式系数的性质 课件(共19张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册【整合课件】6.3.2二项式系数的性质 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 363.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
计数原理
第六章
6.3.2 二项式系数的性质
6.3 二项式定理
课程内容标准 学科素养凝练
1.掌握二项式系数的性质及其应用. 2.掌握“赋值法”并会灵活运用. 在运用二项式系数性质及赋值法求解问题的过程中,提升逻辑推理、数学运算的核心素养.
课前 预习案
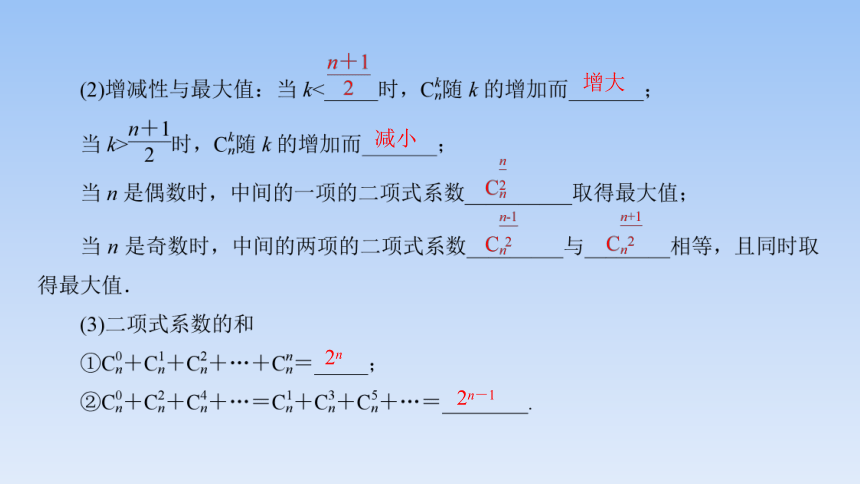
二项式系数的性质
首末两端“等距离”
增大
减小
2n
2n-1
答案 (1)× (2)× (3)×
2.已知(a+b)n展开式中只有第5项的二项式系数最大,则n等于 ( )
A.11 B.10
C.9 D.8
答案 D
3.(1+2x)2n的展开式中,二项式系数最大的项所在的项数是第________项.
答案 n+1
解析 (1+2x)2n的展开式中共有2n+1项,中间一项的系数最大,即第n+1项.
设(1-2x)2 015=a0+a1x+a2x2+…+a2 015·x2 015(x∈R).
(1)求a0+a1+a2+…+a2 015的值;
(2)求a1+a3+a5+…+a2 015的值;
(3)求|a0|+|a1|+|a2|+…+|a2 015|的值.
课堂 探究案
探究一 求展开式系数的和
[变式] 已知条件不变,试求a1+2a2+3a3+…+2 015a2 015的值.
解 ∵(1-2x)2 015=a0+a1x+a2x2+…+a2 015x2 015,
∴两边求导得2 015(1-2x)2 014·(-2)
=0+a1+2a2x+3a3x2+…+2 015a2 015x2 014,
令x=1得,-4 030=a1+2a2+3a3+…+2 015a2 015,
∴a1+2a2+3a3+…+2 015a2 015=-4 030.
[方法总结] “赋值法”的应用
“赋值法”是解决二项展开式中项的系数常用的方法,根据题目要求,灵活赋给字母不同值.一般地,要使展开式中项的关系变为系数的关系,令x=0可得常数项,令x=1可得所有项系数之和,令x=-1可得偶次项系数之和与奇次项系数之和的差.
[训练1] 已知(x-m)7=a0+a1x+a2x2+…a7x7的展开式中x4的系数是-35,则a1+a2+a3+…+a7为多少?
探究二 二项式系数性质的应用
解题程序:
第一步:泛读题目明待求结论:求展开式中二项式系数最大的项和系数最大的项.
第二步:精读题目挖已知条件:二项式各项系数和比各项的二项式系数和大992.
第三步:建立联系寻解题思路:(1)根据已知条件求出n,利用通项公式和二项式系数的性质求解;(2)用通项公式求特定项.
第四步:书写过程养规范习惯.
[方法总结]
1.求二项式系数最大的项,根据二项式系数的性质,当n为奇数时,中间两项的二项式系数最大;当n为偶数时,中间一项的二项式系数最大.
2.求展开式中系数最大项与求二项式系数最大项是不同的,需根据各项系数的正、负变化情况,一般采用列不等式组,解不等式的方法求得.
[训练2] 已知(1+2x)n的展开式所有的二项式系数之和为128.
(1)求展开式中的二项式系数最大项;
(2)求展开式中的系数最大项.
计数原理
第六章
6.3.2 二项式系数的性质
6.3 二项式定理
课程内容标准 学科素养凝练
1.掌握二项式系数的性质及其应用. 2.掌握“赋值法”并会灵活运用. 在运用二项式系数性质及赋值法求解问题的过程中,提升逻辑推理、数学运算的核心素养.
课前 预习案
二项式系数的性质
首末两端“等距离”
增大
减小
2n
2n-1
答案 (1)× (2)× (3)×
2.已知(a+b)n展开式中只有第5项的二项式系数最大,则n等于 ( )
A.11 B.10
C.9 D.8
答案 D
3.(1+2x)2n的展开式中,二项式系数最大的项所在的项数是第________项.
答案 n+1
解析 (1+2x)2n的展开式中共有2n+1项,中间一项的系数最大,即第n+1项.
设(1-2x)2 015=a0+a1x+a2x2+…+a2 015·x2 015(x∈R).
(1)求a0+a1+a2+…+a2 015的值;
(2)求a1+a3+a5+…+a2 015的值;
(3)求|a0|+|a1|+|a2|+…+|a2 015|的值.
课堂 探究案
探究一 求展开式系数的和
[变式] 已知条件不变,试求a1+2a2+3a3+…+2 015a2 015的值.
解 ∵(1-2x)2 015=a0+a1x+a2x2+…+a2 015x2 015,
∴两边求导得2 015(1-2x)2 014·(-2)
=0+a1+2a2x+3a3x2+…+2 015a2 015x2 014,
令x=1得,-4 030=a1+2a2+3a3+…+2 015a2 015,
∴a1+2a2+3a3+…+2 015a2 015=-4 030.
[方法总结] “赋值法”的应用
“赋值法”是解决二项展开式中项的系数常用的方法,根据题目要求,灵活赋给字母不同值.一般地,要使展开式中项的关系变为系数的关系,令x=0可得常数项,令x=1可得所有项系数之和,令x=-1可得偶次项系数之和与奇次项系数之和的差.
[训练1] 已知(x-m)7=a0+a1x+a2x2+…a7x7的展开式中x4的系数是-35,则a1+a2+a3+…+a7为多少?
探究二 二项式系数性质的应用
解题程序:
第一步:泛读题目明待求结论:求展开式中二项式系数最大的项和系数最大的项.
第二步:精读题目挖已知条件:二项式各项系数和比各项的二项式系数和大992.
第三步:建立联系寻解题思路:(1)根据已知条件求出n,利用通项公式和二项式系数的性质求解;(2)用通项公式求特定项.
第四步:书写过程养规范习惯.
[方法总结]
1.求二项式系数最大的项,根据二项式系数的性质,当n为奇数时,中间两项的二项式系数最大;当n为偶数时,中间一项的二项式系数最大.
2.求展开式中系数最大项与求二项式系数最大项是不同的,需根据各项系数的正、负变化情况,一般采用列不等式组,解不等式的方法求得.
[训练2] 已知(1+2x)n的展开式所有的二项式系数之和为128.
(1)求展开式中的二项式系数最大项;
(2)求展开式中的系数最大项.
