人教A版(2019)高中数学选择性必修第三册 6.3.1二项式定理课件 课件(共24张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 6.3.1二项式定理课件 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 11:36:35 | ||
图片预览







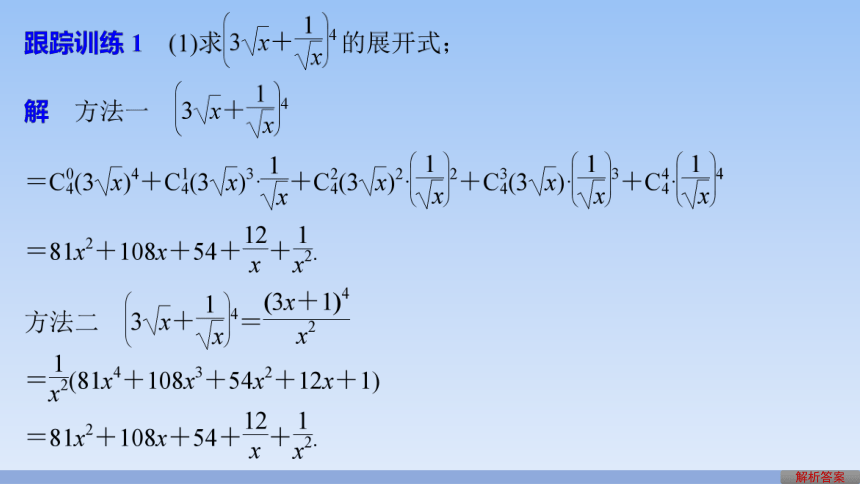
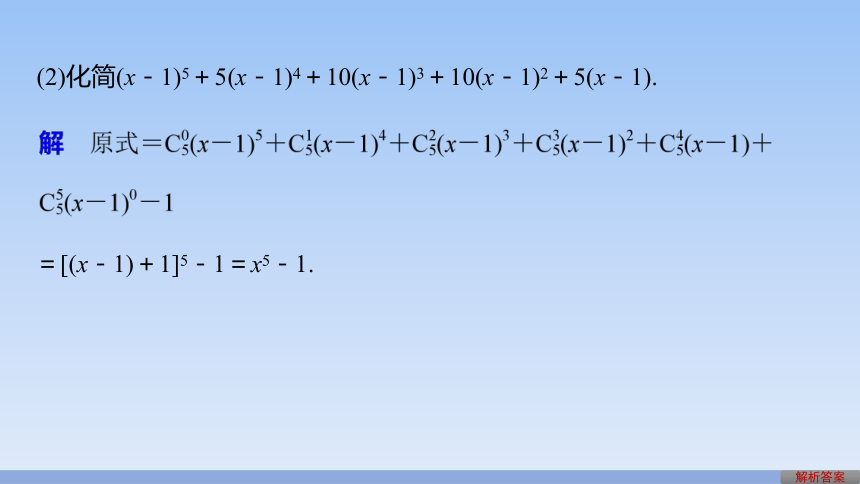
文档简介
(共24张PPT)
6.3.1 二项式定理
1.能用计数原理证明二项式定理.
2.掌握二项式定理及其展开式的通项公式.
3.会用二项式定理解决与二项展开式有关的简单问题.
问题导学
题型探究
达标检测
学习目标
答案
问题导学 新知探究 点点落实
知识点 二项式定理及其相关概念
思考1 我们在初中学习了(a+b)2=a2+2ab+b2,试用多项式的乘法推导(a+b)3,(a+b)4的展开式.
答案 (a+b)3=a3+3a2b+3ab2+b3,(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
思考2 上述两个等式的右侧有何特点?
答案 (a+b)3的展开式有4项,每项的次数是3;
(a+b)4的展开式有5项,每一项的次数为4.
答案
思考3 你能用组合的观点说明(a+b)4是如何展开的吗?
答案 (a+b)4=(a+b)(a+b)(a+b)(a+b).
由多项式的乘法法则知,从每个(a+b)中选a或选b相乘即得展开式中的一项.
思考4 能用类比方法写出(a+b)n(n∈N*)的展开式吗?
二项式定理 公式(a+b)n= ,
称为二项式定理
二项式系数 _________________
通项 Tk+1=________
二项式定理 的特例
答案
返回
类型一 二项式定理的正用、逆用
例1 (1)求(x+2y)4的展开式.
题型探究 重点难点 个个击破
=x4+8x3y+24x2y2+32xy3+16y4.
解析答案
反思与感悟
反思与感悟
1.(a+b)n的二项展开式有n+1项,是和的形式,各项的幂指数规律是:(1)各项的次数等于n;(2)字母a按降幂排列,从第一项起,次数由n逐项减1直到0;字母b按升幂排列,从第一项起,次数由0逐项加1直到n.
2.逆用二项式定理可以化简多项式,体现的是整体思想.注意分析已知多项式的特点,向二项展开式的形式靠拢.
解析答案
解析答案
(2)化简(x-1)5+5(x-1)4+10(x-1)3+10(x-1)2+5(x-1).
=[(x-1)+1]5-1=x5-1.
解析答案
类型二 求二项展开式的特定项
(1)n的值;
所以n2=81,n=9.
解析答案
(2)展开式中含x2的项.
解 设第k+1项含x3项,
所以第二项为含x3的项:
反思与感悟
反思与感悟
解析答案
跟踪训练2 (1)求二项式 的展开式中第6项的二项式系数和第6项的系数;
解 由已知得二项展开式的通项为Tr+1
解析答案
解 设展开式中的第r+1项为含x3的项,则
∴9-2r=3,∴r=3,即展开式中第四项含x3,
解析答案
类型三 求展开式中的特定项
(1)求n;
(2)求含x2的项的系数;
(3)求展开式中所有的有理项.
反思与感悟
解 通项公式为:
(1)∵第6项为常数项,
∵r∈Z,∴k应为偶数.
所以第3项,第6项与第9项为有理项,它们分别为405x2,-61 236,295 245x-2.
k=2,0,-2即r=2,5,8.
反思与感悟
1.求二项展开式的特定项的常见题型
(1)求第k项,Tk= ;
(2)求含xk的项(或xpyq的项);
(3)求常数项;
(4)求有理项.
2.求二项展开式的特定项的常用方法
(1)对于常数项,隐含条件是字母的指数为0(即0次项);
(2)对于有理项,一般是先写出通项公式,其所有的字母的指数恰好都是整数的项.解这类问题必须合并通项公式中同一字母的指数,根据具体要求,令其属于整数,再根据数的整除性来求解;
(3)对于二项展开式中的整式项,其通项公式中同一字母的指数应是非负整数,求解方式与求有理项一致.
反思与感悟
解析答案
当9-2r=3时,解得r=3,代入得x3的系数,
1
解析答案
返回
7
解析答案
达标检测
1.二项式(a+b)2n的展开式的项数是( )
A.2n B.2n+1
C.2n-1 D.2(n+1)
解析 展开式的项数比指数大1.
1
2
3
4
B
解析答案
2.二项式(x+1)n(n∈N*)的展开式中x3的系数为15,则n等于( )
A.4 B.5
C.6 D.7
解得:n=6或-5(舍去).
C
1
2
3
4
解析答案
3.(x-y)(x+y)8的展开式中x2y7的系数为______.(用数字填写答案)
解析 利用二项展开式的通项公式求解.
-20
1
2
3
4
解析答案
1
2
3
4
返回
规律与方法
1.注意区分项的二项式系数与系数的概念.
2.要牢记 是展开式的第k+1项,不要误认为是第k项.
3.求解特定项时必须合并通项公式中同一字母的指数,根据具体要求,令其为特定值.
6.3.1 二项式定理
1.能用计数原理证明二项式定理.
2.掌握二项式定理及其展开式的通项公式.
3.会用二项式定理解决与二项展开式有关的简单问题.
问题导学
题型探究
达标检测
学习目标
答案
问题导学 新知探究 点点落实
知识点 二项式定理及其相关概念
思考1 我们在初中学习了(a+b)2=a2+2ab+b2,试用多项式的乘法推导(a+b)3,(a+b)4的展开式.
答案 (a+b)3=a3+3a2b+3ab2+b3,(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
思考2 上述两个等式的右侧有何特点?
答案 (a+b)3的展开式有4项,每项的次数是3;
(a+b)4的展开式有5项,每一项的次数为4.
答案
思考3 你能用组合的观点说明(a+b)4是如何展开的吗?
答案 (a+b)4=(a+b)(a+b)(a+b)(a+b).
由多项式的乘法法则知,从每个(a+b)中选a或选b相乘即得展开式中的一项.
思考4 能用类比方法写出(a+b)n(n∈N*)的展开式吗?
二项式定理 公式(a+b)n= ,
称为二项式定理
二项式系数 _________________
通项 Tk+1=________
二项式定理 的特例
答案
返回
类型一 二项式定理的正用、逆用
例1 (1)求(x+2y)4的展开式.
题型探究 重点难点 个个击破
=x4+8x3y+24x2y2+32xy3+16y4.
解析答案
反思与感悟
反思与感悟
1.(a+b)n的二项展开式有n+1项,是和的形式,各项的幂指数规律是:(1)各项的次数等于n;(2)字母a按降幂排列,从第一项起,次数由n逐项减1直到0;字母b按升幂排列,从第一项起,次数由0逐项加1直到n.
2.逆用二项式定理可以化简多项式,体现的是整体思想.注意分析已知多项式的特点,向二项展开式的形式靠拢.
解析答案
解析答案
(2)化简(x-1)5+5(x-1)4+10(x-1)3+10(x-1)2+5(x-1).
=[(x-1)+1]5-1=x5-1.
解析答案
类型二 求二项展开式的特定项
(1)n的值;
所以n2=81,n=9.
解析答案
(2)展开式中含x2的项.
解 设第k+1项含x3项,
所以第二项为含x3的项:
反思与感悟
反思与感悟
解析答案
跟踪训练2 (1)求二项式 的展开式中第6项的二项式系数和第6项的系数;
解 由已知得二项展开式的通项为Tr+1
解析答案
解 设展开式中的第r+1项为含x3的项,则
∴9-2r=3,∴r=3,即展开式中第四项含x3,
解析答案
类型三 求展开式中的特定项
(1)求n;
(2)求含x2的项的系数;
(3)求展开式中所有的有理项.
反思与感悟
解 通项公式为:
(1)∵第6项为常数项,
∵r∈Z,∴k应为偶数.
所以第3项,第6项与第9项为有理项,它们分别为405x2,-61 236,295 245x-2.
k=2,0,-2即r=2,5,8.
反思与感悟
1.求二项展开式的特定项的常见题型
(1)求第k项,Tk= ;
(2)求含xk的项(或xpyq的项);
(3)求常数项;
(4)求有理项.
2.求二项展开式的特定项的常用方法
(1)对于常数项,隐含条件是字母的指数为0(即0次项);
(2)对于有理项,一般是先写出通项公式,其所有的字母的指数恰好都是整数的项.解这类问题必须合并通项公式中同一字母的指数,根据具体要求,令其属于整数,再根据数的整除性来求解;
(3)对于二项展开式中的整式项,其通项公式中同一字母的指数应是非负整数,求解方式与求有理项一致.
反思与感悟
解析答案
当9-2r=3时,解得r=3,代入得x3的系数,
1
解析答案
返回
7
解析答案
达标检测
1.二项式(a+b)2n的展开式的项数是( )
A.2n B.2n+1
C.2n-1 D.2(n+1)
解析 展开式的项数比指数大1.
1
2
3
4
B
解析答案
2.二项式(x+1)n(n∈N*)的展开式中x3的系数为15,则n等于( )
A.4 B.5
C.6 D.7
解得:n=6或-5(舍去).
C
1
2
3
4
解析答案
3.(x-y)(x+y)8的展开式中x2y7的系数为______.(用数字填写答案)
解析 利用二项展开式的通项公式求解.
-20
1
2
3
4
解析答案
1
2
3
4
返回
规律与方法
1.注意区分项的二项式系数与系数的概念.
2.要牢记 是展开式的第k+1项,不要误认为是第k项.
3.求解特定项时必须合并通项公式中同一字母的指数,根据具体要求,令其为特定值.
