人教A版(2019)高中数学选择性必修第三册第六章《计数原理》章末复习课件(共17张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册第六章《计数原理》章末复习课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 436.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 11:46:29 | ||
图片预览






文档简介
(共17张PPT)
《计数原理》章末复习
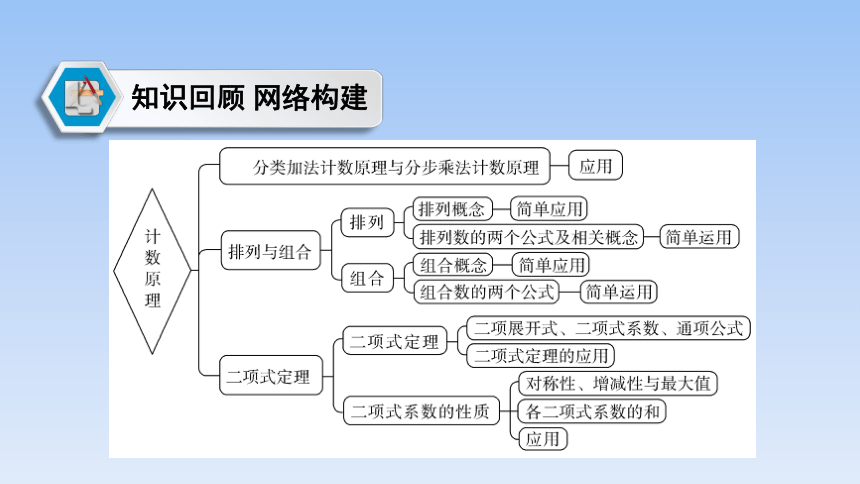
知识回顾 网络构建
一、计数原理的应用
使用两个原理解决问题时应注意的问题
(1)对于一些比较复杂的既要运用分类加法计数原理又要运用分步乘法计数原理的问题,我们可以恰当地画出示意图或列出表格,使问题更加直观、清晰.
(2)当两个原理混合使用时,一般是先分类,在每类方法里再分步.
综合题型 归纳总结
[训练1] 有4部机床,需加工3个不同的零件,其不同的安排方法有 ( )
A.34种 B.43种
C.3×4种 D.44种
答案 B
解析 事件为“加工3个零件”,每个零件都加工完这件事就算完成,应以“每个零件”为分步标准,共3步,而每个零件能在四部机床中的任一台上加工,所以有4种方法,于是安排方法有4×4×4=43.
[训练2] 王华同学有课外参考书若干本,其中有5本不同的外语书,4本不同的数学书,3本不同的物理书,他欲带参考书到图书馆阅读.
(1)若他从这些参考书中带一本去图书馆,有多少种不同的带法?
(2)若带外语、数学、物理参考书各一本,有多少种不同的带法?
(3)若从这些参考书中选2本不同学科的参考书带到图书馆,有多少种不同的带法?
解 (1)完成的事情是带一本书,无论带外语书,还是数学书、物理书,事情都已完成,从而确定为应用分类加法计数原理,结果为5+4+3=12(种).
(2)完成的事情是带3本不同学科的参考书,只有从外语、数学、物理书中各选1本后,才能完成这件事,因此应用分步乘法计数原理,结果为5×4×3=60(种).
(3)选1本外语书和选1本数学书应用分步乘法计数原理,有5×4=20种选法;
同样,选外语书、物理书各1本,有5×3=15种选法;
选数学书、物理书各1本,有4×3=12种选法.
即有三类情况,应用分类加法计数原理,结果为20+15+12=47(种).
二、排列与组合
排列、组合应用题的解题策略
(1)在解决具体问题时,首先必须弄清楚是“分类”还是“分步”,接着还要搞清楚“分类”或者“分步”的具体标准是什么.
(2)区分某一问题是排列还是组合问题,关键看选出的元素与顺序是否有关. 若交换某两个元素的位置对结果产生影响,则是排列问题;若交换任意两个元素的位置对结果没有影响,则是组合问题. 也就是说排列问题与选取元素的顺序有关,组合问题与选取元素的顺序无关.
[训练3] 将5个不同的球放入4个不同的盒子中,每个盒子至少放一个球,则不同放法共有 ( )
A.480种 B.360种
C.240种 D.120种
答案 C
[训练4] 在高三一班元旦晚会上,有6个演唱节目,4个舞蹈节目.
(1)当4个舞蹈节目要排在一起时,有多少种不同的节目安排顺序?
(2)当要求每2个舞蹈节目之间至少安排1个演唱节目时,有多少种不同的节目安排顺序?
(3)若已定好节目单,后来情况有变,需加上诗朗诵和快板2个栏目,但不能改变原来节目的相对顺序,有多少种不同的节目演出顺序?
三、二项式定理的运用
二项式定理的问题类型及解答策略
(1)确定二项式中的有关元素:一般是根据已知条件,列出等式,从而可解得所要求的二项式中的有关元素.
(2)确定二项展开式中的常数项:先写出其通项公式,令未知数的指数为零,从而确定项数,然后代入通项公式,即可确定常数项.
(3)求二项展开式中条件项的系数:先写出其通项公式,再由条件确定项数,然后代入通项公式求出此项的系数.
(4)求二项展开式中各项系数的和差:赋值代入.
(5)确定二项展开式中的系数最大或最小项:利用二项式系数的性质.
四、二项式定理中的赋值问题
二项式定理中赋值法的应用
(1)解决的问题:与二项式系数有关,包括求展开式中二项式系数最大的项、各项的二项式系数或系数的和、奇数项或者偶数项的二项式系数或系数的和以及各项系数的绝对值的和.
(2)应用技巧:通过观察展开式右边的结构特点和所求式子的关系,确定给字母所赋的值,有时赋值后得到的式子比所求式子多一项或少一项,此时要专门求出这一项,而在求奇数项或者偶数项的二项式系数或系数的和时,往往要两次赋值,再由方程组求出结果.
[训练7] 已知(1-2x)6=a0+a1x+a2x2+…+a6x6,则|a0|+|a1|+|a2|+…+|a6|=
( )
A.1 B.-1
C.36 D.26
答案 C
解析 由已知展开式中a0,a2,a4,a6大于零,a1,a3,a5小于零.
所以|a0|+|a1|+|a2|+…+|a6|=a0-a1+a2-a3+a4-a5+a6.
令x=-1,得a0-a1+a2-a3+a4-a5+a6=36.
所以|a0|+|a1|+|a2|+…+|a6|=36.
[训练8] 已知(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11,那么a1+a2+…+a11=____________.
答案 -65
解析 令x=0,得a0=1;令x=1,得a0+a1+a2+…+a11=-64.
所以a1+a2+…+a11=-65.
《计数原理》章末复习
知识回顾 网络构建
一、计数原理的应用
使用两个原理解决问题时应注意的问题
(1)对于一些比较复杂的既要运用分类加法计数原理又要运用分步乘法计数原理的问题,我们可以恰当地画出示意图或列出表格,使问题更加直观、清晰.
(2)当两个原理混合使用时,一般是先分类,在每类方法里再分步.
综合题型 归纳总结
[训练1] 有4部机床,需加工3个不同的零件,其不同的安排方法有 ( )
A.34种 B.43种
C.3×4种 D.44种
答案 B
解析 事件为“加工3个零件”,每个零件都加工完这件事就算完成,应以“每个零件”为分步标准,共3步,而每个零件能在四部机床中的任一台上加工,所以有4种方法,于是安排方法有4×4×4=43.
[训练2] 王华同学有课外参考书若干本,其中有5本不同的外语书,4本不同的数学书,3本不同的物理书,他欲带参考书到图书馆阅读.
(1)若他从这些参考书中带一本去图书馆,有多少种不同的带法?
(2)若带外语、数学、物理参考书各一本,有多少种不同的带法?
(3)若从这些参考书中选2本不同学科的参考书带到图书馆,有多少种不同的带法?
解 (1)完成的事情是带一本书,无论带外语书,还是数学书、物理书,事情都已完成,从而确定为应用分类加法计数原理,结果为5+4+3=12(种).
(2)完成的事情是带3本不同学科的参考书,只有从外语、数学、物理书中各选1本后,才能完成这件事,因此应用分步乘法计数原理,结果为5×4×3=60(种).
(3)选1本外语书和选1本数学书应用分步乘法计数原理,有5×4=20种选法;
同样,选外语书、物理书各1本,有5×3=15种选法;
选数学书、物理书各1本,有4×3=12种选法.
即有三类情况,应用分类加法计数原理,结果为20+15+12=47(种).
二、排列与组合
排列、组合应用题的解题策略
(1)在解决具体问题时,首先必须弄清楚是“分类”还是“分步”,接着还要搞清楚“分类”或者“分步”的具体标准是什么.
(2)区分某一问题是排列还是组合问题,关键看选出的元素与顺序是否有关. 若交换某两个元素的位置对结果产生影响,则是排列问题;若交换任意两个元素的位置对结果没有影响,则是组合问题. 也就是说排列问题与选取元素的顺序有关,组合问题与选取元素的顺序无关.
[训练3] 将5个不同的球放入4个不同的盒子中,每个盒子至少放一个球,则不同放法共有 ( )
A.480种 B.360种
C.240种 D.120种
答案 C
[训练4] 在高三一班元旦晚会上,有6个演唱节目,4个舞蹈节目.
(1)当4个舞蹈节目要排在一起时,有多少种不同的节目安排顺序?
(2)当要求每2个舞蹈节目之间至少安排1个演唱节目时,有多少种不同的节目安排顺序?
(3)若已定好节目单,后来情况有变,需加上诗朗诵和快板2个栏目,但不能改变原来节目的相对顺序,有多少种不同的节目演出顺序?
三、二项式定理的运用
二项式定理的问题类型及解答策略
(1)确定二项式中的有关元素:一般是根据已知条件,列出等式,从而可解得所要求的二项式中的有关元素.
(2)确定二项展开式中的常数项:先写出其通项公式,令未知数的指数为零,从而确定项数,然后代入通项公式,即可确定常数项.
(3)求二项展开式中条件项的系数:先写出其通项公式,再由条件确定项数,然后代入通项公式求出此项的系数.
(4)求二项展开式中各项系数的和差:赋值代入.
(5)确定二项展开式中的系数最大或最小项:利用二项式系数的性质.
四、二项式定理中的赋值问题
二项式定理中赋值法的应用
(1)解决的问题:与二项式系数有关,包括求展开式中二项式系数最大的项、各项的二项式系数或系数的和、奇数项或者偶数项的二项式系数或系数的和以及各项系数的绝对值的和.
(2)应用技巧:通过观察展开式右边的结构特点和所求式子的关系,确定给字母所赋的值,有时赋值后得到的式子比所求式子多一项或少一项,此时要专门求出这一项,而在求奇数项或者偶数项的二项式系数或系数的和时,往往要两次赋值,再由方程组求出结果.
[训练7] 已知(1-2x)6=a0+a1x+a2x2+…+a6x6,则|a0|+|a1|+|a2|+…+|a6|=
( )
A.1 B.-1
C.36 D.26
答案 C
解析 由已知展开式中a0,a2,a4,a6大于零,a1,a3,a5小于零.
所以|a0|+|a1|+|a2|+…+|a6|=a0-a1+a2-a3+a4-a5+a6.
令x=-1,得a0-a1+a2-a3+a4-a5+a6=36.
所以|a0|+|a1|+|a2|+…+|a6|=36.
[训练8] 已知(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11,那么a1+a2+…+a11=____________.
答案 -65
解析 令x=0,得a0=1;令x=1,得a0+a1+a2+…+a11=-64.
所以a1+a2+…+a11=-65.
