人教A版(2019)高中数学选择性必修第三册7.1.1 《条件概率》名师课件(共27张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册7.1.1 《条件概率》名师课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 11:53:42 | ||
图片预览







文档简介
(共27张PPT)
复习引入
引例1 某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,如果已知某天的空气质量为优良,则随后一天的空气质量也为优良的概率是否仍然是0.75?如果不是,那么比0.75大还是小?
人教A版同步教材名师课件
条件概率
学习目标
学 习 目 标 核心素养
初步了解和体会条件概率的概念 数学抽象
能利用条件概率的公式解决简单的条件概率问题 数学建模
了解条件概率的性质 逻辑推理
学习目标
学习目标:
1.了解条件概率的概念.
2.掌握求条件概率的两种方法.
3.能利用条件概率公式解一些简单的实际问题.
学科核心素养:
通过创设教学情境,培养学生学习数学的良好思维习惯和兴趣.通过采用引导发现、自主探究、问题引领等方法,让学生的思维活动在教师的引导和问题的引领下层层展开,加深学生对从特殊到一般的思想认知规律的认识,提高学生抽象概括的能力,培养学生对数学概念的理解能力和应用能力.
探究新知
引例2 箱子里有红、黄、蓝三个小球,现由甲、乙2名同学依次无放回地摸球,问乙同学摸到红球的概率是多少?
引例3 箱子里有红、黄、蓝三个小球,现由甲、乙2名同学依次无放回地摸球,如果已知甲没有摸到红球,那么乙摸到红球的概率是变大了还是变小了?又是多少?
上面两个问题有什么共同特征?可以用怎样的数学模型来刻画?
探究新知
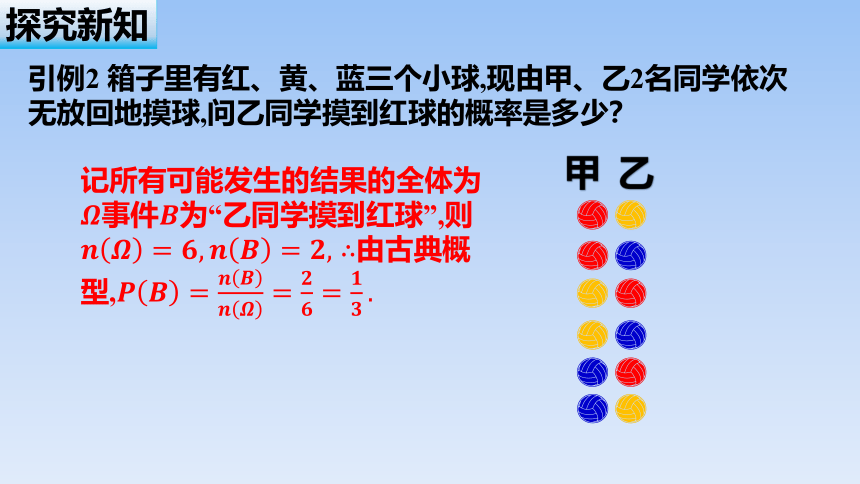
引例2 箱子里有红、黄、蓝三个小球,现由甲、乙2名同学依次无放回地摸球,问乙同学摸到红球的概率是多少?
甲 乙
记所有可能发生的结果的全体为事件为“乙同学摸到红球”,则 由古典概型,
探究新知
引例3 箱子里有红、黄、蓝三个小球,现由甲、乙2名同学依次无放回地摸球,如果已知甲没有摸到红球,那么乙摸到红球的概率是变大了还是变小了?又是多少?
甲 乙
记所有可能发生的结果的全体为事件为“乙同学摸到红球”,则 由古典概型,
探究新知
条件概率的概念
一般地,设为两个事件,且,称
为事件发生的条件下,事件B发生的条件概率.
读作发生的条件下发生的概率.
探究新知
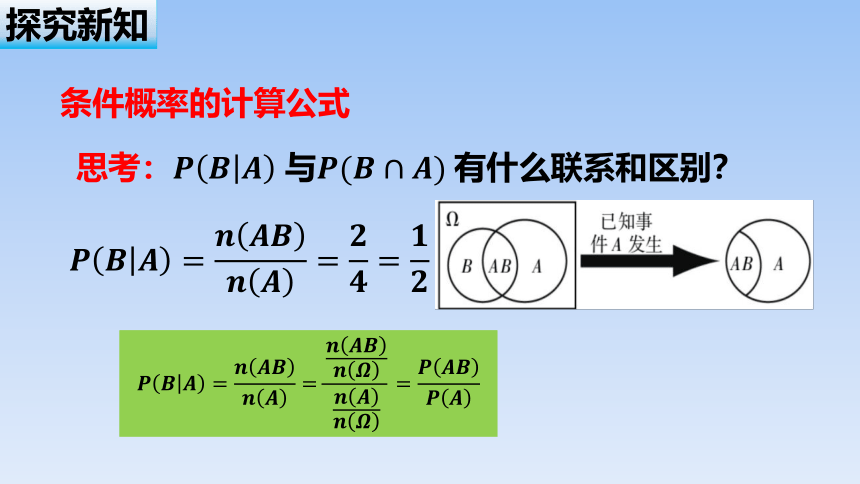
条件概率的计算公式
思考: 与有什么联系和区别?
典例讲解
例1、一个袋中有2个黑球和3个白球,如果不放回地抽取两个球,记事件“第一次抽到黑球”为;事件“第二次抽到黑球”为.
(1)分别求事件发生的概率;
(2)求.
由古典概型的概率公式可知
(1)
(2).
解析
方法归纳
1.用定义法求条件概率的步骤
(1)分析题意,弄清概率模型;
(2)计算;
(3)代入公式求.
2.在(2)题中,首先结合古典概型分别求出事件的概率,从而求出,揭示出和三者之间的关系.
变式训练
1.甲、乙两市都位于长江下游,根据一百多年来的气象记录,知道一年中下雨天的比例甲市占20%,乙市占18%,两地同时下雨占12%,记,则________,________.
由公式
解析
典例讲解
设第1次抽到舞蹈节目为事件,第2次抽到舞蹈节目为事件,则第1次和第2次都抽到舞蹈节目为事件.
(1)从6个节目中不放回地依次抽取2个的事件数为,
根据分步计数原理,于是
(2)因为,于是
例2.现有6个节目准备参加比赛,其中4个舞蹈节目,2个语言类节目,如果不放回地依次抽取2个节目,求:
(1)第1次抽到舞蹈节目的概率;
(2)第1次和第2次都抽到舞蹈节目的概率;
(3)在第1次抽到舞蹈节目的条件下,第2次抽到舞蹈节目的概率.
解析
典例讲解
(3)法一:由(1)(2)可得,在第1次抽到舞蹈节目的条件下,第2次抽到舞蹈节目的概率为
.
法二:因为,
所以.
例2.现有6个节目准备参加比赛,其中4个舞蹈节目,2个语言类节目,如果不放回地依次抽取2个节目,求:
(1)第1次抽到舞蹈节目的概率;
(2)第1次和第2次都抽到舞蹈节目的概率;
(3)在第1次抽到舞蹈节目的条件下,第2次抽到舞蹈节目的概率.
解析
方法归纳
1.本题第(3)问给出了两种求条件概率的方法,法一为定义法,法二利用基本事件个数直接作商,是一种重要的求条件概率的方法.
2.计算条件概率的方法
(1)在缩小后的样本空间中计算事件发生的概率,即.
(2)在原样本空间中,先计算,,再利用公式计算求得.
(3)条件概率的算法:已知事件发生,在此条件下事件发生,即事件发生,要求,相当于把看作新的基本事件空间计算事件发生的概率,即.
变式训练
解析
2.本例条件不变,试求在第1次抽到舞蹈节目的条件下,第2次抽到语言类节目的概率.
设第1次抽到舞蹈节目为事件,第2次抽到语言类节目为事件,则第1次抽到舞蹈节目、第2次抽到语言类节目为事件.
典例讲解
例3. 一批同型号产品由甲、乙两厂生产,产品结构如下表: (1)从这批产品中随意地取一件,则这件产
品恰好是次品的概率是________;
(2)已知取出的产品是甲厂生产的,则这件产
品恰好是次品的概率是________.
(1)从这批产品中随意地取一件,则这件产品恰好是次品的概率是.
(2)法一:已知取出的产品是甲厂生产的,则这件产品恰好是次品的概率是.
解析
典例讲解
例3. 一批同型号产品由甲、乙两厂生产,产品结构如下表: (1)从这批产品中随意地取一件,则这件产
品恰好是次品的概率是________;
(2)已知取出的产品是甲厂生产的,则这件产
品恰好是次品的概率是________.
法二:设“取出的产品是甲厂生产的”,“取出的产品为甲厂的次品”,则,,所以这件产品恰好是甲厂生产的次品的概率是.
解析
方法归纳
分解计算,代入求值,为了求比较复杂事件的概率,一般先把它分解成两个(或若干个)互不相容的较简单的事件之和,求出这些简单事件的概率,再利用加法公式即得所求的复杂事件的概率.
条件概率的解题策略
变式训练
设“任选一人是男人”为事件, “任选一人是女人”为事件, “任选一人是色盲”为事件.
(1)此人患色盲的概率
.
(2).
3.已知男人中有5%患色盲,女人中有0.25%患色盲,从100个男人和100个女人中任选一人.
(1)求此人患色盲的概率;
(2)如果此人是色盲,求此人是男人的概率.
解析
素养提炼
一般地,当事件发生的概率大于0时,已知事件发生的条件下事件A发生的概率,称为条件概率.一般地,每一个随机试验都是在一定条件下进行的,而这里所说的条件概率,则是当试验结果的一部分信息已知(即在原随机试验的条件上,再加上一定的条件),求另一事件在此条件下发生的概率在事件发生的条件下,事件发生的概率,用符号表示为把由事件和同时发生所构成的事件,称为与的交(或积),记作(或)注意区分交事件的概率与条件概率.
条件概率的理解
当堂练习
1.已知,则等于( )
A. B. C. D.
C
2.把一枚硬币投掷两次,事件{第一次出现正面},{第二次出现正面},则________.
由,得
解析
∵.
解析
3.抛掷骰子2次,每次结果用表示,其中分别表示第一次、第二次骰子的点数.若设,则________.
当堂练习
∵,
∴.
解析
当堂练习
4.一个口袋内装有2个白球和2个黑球,那么:
(1)先摸出1个白球不放回,再摸出1个白球的概率是多少?
(2)先摸出1个白球后放回,再摸出1个白球的概率是多少?
(1)设“先摸出1个白球不放回”为事件,“再摸出1个白球”为事件,则“先后两次摸出白球”为事件,“先摸一球不放回,再摸一球”共有4×3种结果,所以,,所以.所以先摸出1个白球不放回,再摸出1个白球的概率为.
解析
当堂练习
4.一个口袋内装有2个白球和2个黑球,那么:
(1)先摸出1个白球不放回,再摸出1个白球的概率是多少?
(2)先摸出1个白球后放回,再摸出1个白球的概率是多少?
解析
(2)设“先摸出1个白球放回”为事件,“再摸出1个白球”为事件,“两次都摸出白球”为事件,
,所以.所以先摸出1个白球后放回,再摸出1个白球的概率为.
归纳小结
名称 定义 符号表示 计算公式
条件概率 ________
发生
作 业
课本P48练习:2,3
复习引入
引例1 某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,如果已知某天的空气质量为优良,则随后一天的空气质量也为优良的概率是否仍然是0.75?如果不是,那么比0.75大还是小?
人教A版同步教材名师课件
条件概率
学习目标
学 习 目 标 核心素养
初步了解和体会条件概率的概念 数学抽象
能利用条件概率的公式解决简单的条件概率问题 数学建模
了解条件概率的性质 逻辑推理
学习目标
学习目标:
1.了解条件概率的概念.
2.掌握求条件概率的两种方法.
3.能利用条件概率公式解一些简单的实际问题.
学科核心素养:
通过创设教学情境,培养学生学习数学的良好思维习惯和兴趣.通过采用引导发现、自主探究、问题引领等方法,让学生的思维活动在教师的引导和问题的引领下层层展开,加深学生对从特殊到一般的思想认知规律的认识,提高学生抽象概括的能力,培养学生对数学概念的理解能力和应用能力.
探究新知
引例2 箱子里有红、黄、蓝三个小球,现由甲、乙2名同学依次无放回地摸球,问乙同学摸到红球的概率是多少?
引例3 箱子里有红、黄、蓝三个小球,现由甲、乙2名同学依次无放回地摸球,如果已知甲没有摸到红球,那么乙摸到红球的概率是变大了还是变小了?又是多少?
上面两个问题有什么共同特征?可以用怎样的数学模型来刻画?
探究新知
引例2 箱子里有红、黄、蓝三个小球,现由甲、乙2名同学依次无放回地摸球,问乙同学摸到红球的概率是多少?
甲 乙
记所有可能发生的结果的全体为事件为“乙同学摸到红球”,则 由古典概型,
探究新知
引例3 箱子里有红、黄、蓝三个小球,现由甲、乙2名同学依次无放回地摸球,如果已知甲没有摸到红球,那么乙摸到红球的概率是变大了还是变小了?又是多少?
甲 乙
记所有可能发生的结果的全体为事件为“乙同学摸到红球”,则 由古典概型,
探究新知
条件概率的概念
一般地,设为两个事件,且,称
为事件发生的条件下,事件B发生的条件概率.
读作发生的条件下发生的概率.
探究新知
条件概率的计算公式
思考: 与有什么联系和区别?
典例讲解
例1、一个袋中有2个黑球和3个白球,如果不放回地抽取两个球,记事件“第一次抽到黑球”为;事件“第二次抽到黑球”为.
(1)分别求事件发生的概率;
(2)求.
由古典概型的概率公式可知
(1)
(2).
解析
方法归纳
1.用定义法求条件概率的步骤
(1)分析题意,弄清概率模型;
(2)计算;
(3)代入公式求.
2.在(2)题中,首先结合古典概型分别求出事件的概率,从而求出,揭示出和三者之间的关系.
变式训练
1.甲、乙两市都位于长江下游,根据一百多年来的气象记录,知道一年中下雨天的比例甲市占20%,乙市占18%,两地同时下雨占12%,记,则________,________.
由公式
解析
典例讲解
设第1次抽到舞蹈节目为事件,第2次抽到舞蹈节目为事件,则第1次和第2次都抽到舞蹈节目为事件.
(1)从6个节目中不放回地依次抽取2个的事件数为,
根据分步计数原理,于是
(2)因为,于是
例2.现有6个节目准备参加比赛,其中4个舞蹈节目,2个语言类节目,如果不放回地依次抽取2个节目,求:
(1)第1次抽到舞蹈节目的概率;
(2)第1次和第2次都抽到舞蹈节目的概率;
(3)在第1次抽到舞蹈节目的条件下,第2次抽到舞蹈节目的概率.
解析
典例讲解
(3)法一:由(1)(2)可得,在第1次抽到舞蹈节目的条件下,第2次抽到舞蹈节目的概率为
.
法二:因为,
所以.
例2.现有6个节目准备参加比赛,其中4个舞蹈节目,2个语言类节目,如果不放回地依次抽取2个节目,求:
(1)第1次抽到舞蹈节目的概率;
(2)第1次和第2次都抽到舞蹈节目的概率;
(3)在第1次抽到舞蹈节目的条件下,第2次抽到舞蹈节目的概率.
解析
方法归纳
1.本题第(3)问给出了两种求条件概率的方法,法一为定义法,法二利用基本事件个数直接作商,是一种重要的求条件概率的方法.
2.计算条件概率的方法
(1)在缩小后的样本空间中计算事件发生的概率,即.
(2)在原样本空间中,先计算,,再利用公式计算求得.
(3)条件概率的算法:已知事件发生,在此条件下事件发生,即事件发生,要求,相当于把看作新的基本事件空间计算事件发生的概率,即.
变式训练
解析
2.本例条件不变,试求在第1次抽到舞蹈节目的条件下,第2次抽到语言类节目的概率.
设第1次抽到舞蹈节目为事件,第2次抽到语言类节目为事件,则第1次抽到舞蹈节目、第2次抽到语言类节目为事件.
典例讲解
例3. 一批同型号产品由甲、乙两厂生产,产品结构如下表: (1)从这批产品中随意地取一件,则这件产
品恰好是次品的概率是________;
(2)已知取出的产品是甲厂生产的,则这件产
品恰好是次品的概率是________.
(1)从这批产品中随意地取一件,则这件产品恰好是次品的概率是.
(2)法一:已知取出的产品是甲厂生产的,则这件产品恰好是次品的概率是.
解析
典例讲解
例3. 一批同型号产品由甲、乙两厂生产,产品结构如下表: (1)从这批产品中随意地取一件,则这件产
品恰好是次品的概率是________;
(2)已知取出的产品是甲厂生产的,则这件产
品恰好是次品的概率是________.
法二:设“取出的产品是甲厂生产的”,“取出的产品为甲厂的次品”,则,,所以这件产品恰好是甲厂生产的次品的概率是.
解析
方法归纳
分解计算,代入求值,为了求比较复杂事件的概率,一般先把它分解成两个(或若干个)互不相容的较简单的事件之和,求出这些简单事件的概率,再利用加法公式即得所求的复杂事件的概率.
条件概率的解题策略
变式训练
设“任选一人是男人”为事件, “任选一人是女人”为事件, “任选一人是色盲”为事件.
(1)此人患色盲的概率
.
(2).
3.已知男人中有5%患色盲,女人中有0.25%患色盲,从100个男人和100个女人中任选一人.
(1)求此人患色盲的概率;
(2)如果此人是色盲,求此人是男人的概率.
解析
素养提炼
一般地,当事件发生的概率大于0时,已知事件发生的条件下事件A发生的概率,称为条件概率.一般地,每一个随机试验都是在一定条件下进行的,而这里所说的条件概率,则是当试验结果的一部分信息已知(即在原随机试验的条件上,再加上一定的条件),求另一事件在此条件下发生的概率在事件发生的条件下,事件发生的概率,用符号表示为把由事件和同时发生所构成的事件,称为与的交(或积),记作(或)注意区分交事件的概率与条件概率.
条件概率的理解
当堂练习
1.已知,则等于( )
A. B. C. D.
C
2.把一枚硬币投掷两次,事件{第一次出现正面},{第二次出现正面},则________.
由,得
解析
∵.
解析
3.抛掷骰子2次,每次结果用表示,其中分别表示第一次、第二次骰子的点数.若设,则________.
当堂练习
∵,
∴.
解析
当堂练习
4.一个口袋内装有2个白球和2个黑球,那么:
(1)先摸出1个白球不放回,再摸出1个白球的概率是多少?
(2)先摸出1个白球后放回,再摸出1个白球的概率是多少?
(1)设“先摸出1个白球不放回”为事件,“再摸出1个白球”为事件,则“先后两次摸出白球”为事件,“先摸一球不放回,再摸一球”共有4×3种结果,所以,,所以.所以先摸出1个白球不放回,再摸出1个白球的概率为.
解析
当堂练习
4.一个口袋内装有2个白球和2个黑球,那么:
(1)先摸出1个白球不放回,再摸出1个白球的概率是多少?
(2)先摸出1个白球后放回,再摸出1个白球的概率是多少?
解析
(2)设“先摸出1个白球放回”为事件,“再摸出1个白球”为事件,“两次都摸出白球”为事件,
,所以.所以先摸出1个白球后放回,再摸出1个白球的概率为.
归纳小结
名称 定义 符号表示 计算公式
条件概率 ________
发生
作 业
课本P48练习:2,3
