人教A版(2019)高中数学选择性必修第三册7.2《离散型随机变量及其分布列》名师课件(共30张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册7.2《离散型随机变量及其分布列》名师课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
复习引入
如果随机试验的结果可以用一个变量来表示,(或随着试验结果变化而变化的变量),那么这样的变量叫做随机变量.
随机变量常用希腊字母等表示.
1.随机变量
2.离散型随机变量
所有取值可以一一列出的随机变量,称为离散型随机变量.
人教A版同步教材名师课件
离散型随机变量及其分布列
学习目标
学 习 目 标 核心素养
理解离散型随机变量的分布列及两点分布的意义 数学抽象
会求某些简单的离散型随机变量的分布列 数学运算
掌握离散型随机变量的分布列的两个基本性质,并会用它来解决一些简单的问题 逻辑推理
学习目标
学习目标:
1.理解取有限值的离散型随机变量及其分布列的概念与性质.
2.会求出某些简单的离散型随机变量的分布列.
3.理解二点分布的定义,并能简单的运用.
学科核心素养:
经历利用离散型随机变量描述和分析某些随机现象的过程,能用所学知识解决一些简单的实际问题,培养对数学知识的整合能力,发展逻辑推理、数学抽象与数学运算等核心素养.
探究新知
抛掷一枚骰子,所得的点数有哪些值?取每个值的概率是多少?
解:
则
1
2
6
5
4
3
⑵求出了的每一个取值的概率.
⑴列出了随机变量的所有取值.
的取值有1、2、3、4、5、6
探究新知
离散型随机变量的分布列
1、一般地,当随机变量的所有可能的取值范围是时,如果对任意的概率为都是已知的,则称的频率分布是已知的.离散型随机变量的频率分布可以用如下形式的表格表示,这个表格称为的概率分布或分布列
···
···
···
···
探究新知
注:
1、分布列的构成
2、分布列的性质:
⑴列出了随机变量的所有取值.
⑵求出了的每一个取值的概率.
⑵ .
⑴.
探究新知
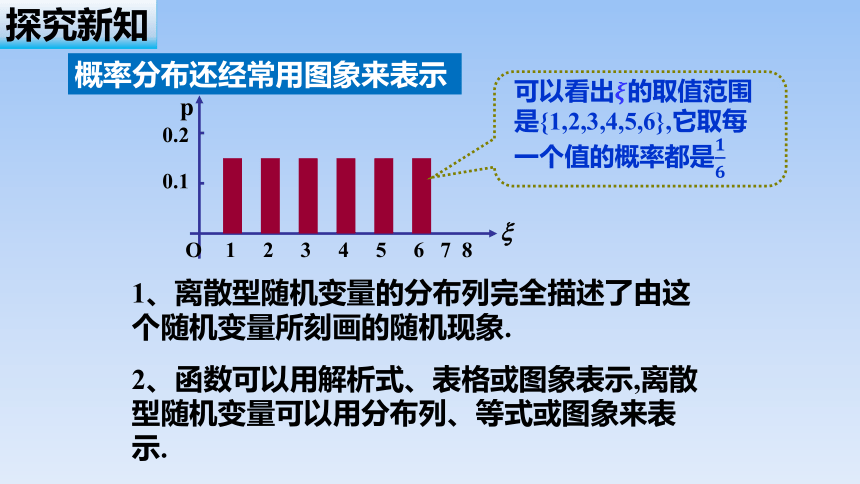
概率分布还经常用图象来表示
O
1 2 3 4 5 6 7 8
p
0.1
0.2
1、离散型随机变量的分布列完全描述了由这个随机变量所刻画的随机现象.
2、函数可以用解析式、表格或图象表示,离散型随机变量可以用分布列、等式或图象来表示.
可以看出的取值范围是{1,2,3,4,5,6},它取每一个值的概率都是
典例讲解
例1、设随机变量X的分布列为,求:
(1)或;
(2).
(1)∵
∴,
则或
.
解析
典例讲解
例1、设随机变量X的分布列为,求:
(1)或;
(2).
(2)由,
可得
.
解析
方法归纳
利用分布列及其性质解题时要注意以下两个问题:
(1)的各个取值表示的事件是互斥的.
(2)不仅要注意 ,而且要注意.
变式训练
1.若离散型随机变量的分布列为:
求常数及相应的分布列.
由分布列的性质可知:,即,解得或,又因,即,故.所以,此时,.所以随机变量的分布列为:
解析
0 1
典例讲解
随机变量的可能取值为3,4,5,6.
从袋中随机取3个球,包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为.
从而有
,
例2.口袋中有6个同样大小的黑球,编号为1,2,3,4,5,6,现从中随机取出3个球,用表示取出的最大号码,求的分布列.
解析
典例讲解
,
所以随机变量的分布列为
例2.口袋中有6个同样大小的黑球,编号为1,2,3,4,5,6,现从中随机取出3个球,用表示取出的最大号码,求的分布列.
解析
X 3 4 5 6
P
方法归纳
1.求离散型随机变量的分布列的步骤
(1)找出随机变量的所有可能的取值.
(2)求出取每一个值的概率.
(3)列出表格.
2.求离散型随机变量分布列时应注意的问题
(1)确定离散型随机变量的分布列的关键是要搞清取每一个值对应的随机事件,进一步利用排列、组合知识求出取每一个值的概率.对于随机变量取值较多时,应由简单情况先导出一般的通式,从而简化过程.
(2)在求离散型随机变量的分布列时,要充分利用分布列的性质,这样不但可以减少运算量,还可验证分布列是否正确.
变式训练
解析
2.从装有6个白球,4个黑球和2个黄球的箱中随机地取出两个球,规定每取出一个黑球赢2元,而每取出一个白球输1元,取出黄球无输赢,以表示赢得的钱数,随机变量可以取哪些值呢?求的分布列.
从箱中取两个球的情形有以下6种:
{2白},{1白1黄},{1白1黑},{2黄},{1黑1黄},{2黑}.
当取到2白时,结果输2元,随机变量;
当取到1白1黄时,输1元,随机变量;
当取到1白1黑时,随机变量;
当取到2黄时,;
当取到1黑1黄时,;
变式训练
解析
2.从装有6个白球,4个黑球和2个黄球的箱中随机地取出两个球,规定每取出一个黑球赢2元,而每取出一个白球输1元,取出黄球无输赢,以表示赢得的钱数,随机变量可以取哪些值呢?求的分布列.
当取到2黑时,.
则的可能取值为.
变式训练
解析
2.从装有6个白球,4个黑球和2个黄球的箱中随机地取出两个球,规定每取出一个黑球赢2元,而每取出一个白球输1元,取出黄球无输赢,以表示赢得的钱数,随机变量可以取哪些值呢?求的分布列.
从而得到X的分布列如下:
-2 -1 0 1 2 4
探究新知
1.利用随机变量研究一类问题,如抽取的奖券是否中奖,买回的一件产品是否为正品,新生婴儿的性别,投篮是否命中等,这些问题有什么共同点?
【提示】这些问题的共同点是随机试验只有两个可能的结果.定义一个随机变量,使其中一个结果对应于1,另一个结果对应于0,即得到服从二点分布的随机变量.
问题
一般地,如果随机变量的分布列能写成上述表格的形式,则称这个随机变量服从参数的两点分布(或0-1分布).
1 0
探究新知
2.只取两个不同值的随机变量是否一定服从二点分布?
【提示】不一定.如随机变量的分布列由下表给出
不服从二点分布,因为的取值不是0或1 .
2 5
0.3 0.7
典例讲解
例3.袋内有10个白球,5个红球,从中摸出2个球,记求的分布列.
由题设可知服从二点分布.
.
∴的分布列为
解析
0 1
方法归纳
1.看取值:随机变量只取两个值0和1.
2.验概率:检验是否成立.
如果一个分布满足以上两点,则该分布是二点分布,否则不是二点分布.
两步法判断一个分布是否为二点分布
变式训练
由离散型随机变量分布列的性质可知,,解得.
3.若离散型随机变量的分布列为
解析
则( )
A. B. C. D.
0 1
C
素养提炼
(1)离散型随机变量的分布列不仅能清楚地反映离散型随机变量的所有可能取值,而且能清楚地看到取每一个值的概率的大小,从而反映了离散型随机变量在随机试验中取值的分布情况
(2)由于离散型随机变量的各个取值之间彼此互斥,因此离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和
离散型随机变量的分布列
当堂练习
1.设是一个离散型随机变量,其分布列为
A
则常数的值为( )
A. B. C.或 D. 或
0 1
由离散型随机变量分布列的性质可得
,,解得
解析
2.随机变量的分布列如下:
当堂练习
由分布列的性质得
,
解得.故.
解析
则________,________.
1 2 3 4 5 6
0.2 0.35 0.1 0.15 0.2
当堂练习
3.在学校组织的足球比赛中,某班要与其他4个班级各赛一场,在这4场比赛的任意一场中,此班级每次胜、负、平的概率相等.已知当这4场比赛结束后,该班胜场多于负场.
(1)求该班级胜场多于负场的所有可能的个数和;
(2)若胜场次数为,求的分布列.
解析
(1)若胜一场,则其余为平,共有种情况;若胜两场,则其余两场为一负一平或两平,共有种情况;若胜三场,则其余一场为负或平,共有种情况;若胜四场,则只有一种情况.综上,共有31种情况.
当堂练习
3.在学校组织的足球比赛中,某班要与其他4个班级各赛一场,在这4场比赛的任意一场中,此班级每次胜、负、平的概率相等.已知当这4场比赛结束后,该班胜场多于负场.
(1)求该班级胜场多于负场的所有可能的个数和;
(2)若胜场次数为,求的分布列.
解析
(2) 的可能取值为1,2,3,4,
所以的分布列为
1 2 3 4
归纳小结
离散型随机变量的分布列
特殊分布
定义
性质
求法
二点分布
作 业
课本P60页练习:3,4
复习引入
如果随机试验的结果可以用一个变量来表示,(或随着试验结果变化而变化的变量),那么这样的变量叫做随机变量.
随机变量常用希腊字母等表示.
1.随机变量
2.离散型随机变量
所有取值可以一一列出的随机变量,称为离散型随机变量.
人教A版同步教材名师课件
离散型随机变量及其分布列
学习目标
学 习 目 标 核心素养
理解离散型随机变量的分布列及两点分布的意义 数学抽象
会求某些简单的离散型随机变量的分布列 数学运算
掌握离散型随机变量的分布列的两个基本性质,并会用它来解决一些简单的问题 逻辑推理
学习目标
学习目标:
1.理解取有限值的离散型随机变量及其分布列的概念与性质.
2.会求出某些简单的离散型随机变量的分布列.
3.理解二点分布的定义,并能简单的运用.
学科核心素养:
经历利用离散型随机变量描述和分析某些随机现象的过程,能用所学知识解决一些简单的实际问题,培养对数学知识的整合能力,发展逻辑推理、数学抽象与数学运算等核心素养.
探究新知
抛掷一枚骰子,所得的点数有哪些值?取每个值的概率是多少?
解:
则
1
2
6
5
4
3
⑵求出了的每一个取值的概率.
⑴列出了随机变量的所有取值.
的取值有1、2、3、4、5、6
探究新知
离散型随机变量的分布列
1、一般地,当随机变量的所有可能的取值范围是时,如果对任意的概率为都是已知的,则称的频率分布是已知的.离散型随机变量的频率分布可以用如下形式的表格表示,这个表格称为的概率分布或分布列
···
···
···
···
探究新知
注:
1、分布列的构成
2、分布列的性质:
⑴列出了随机变量的所有取值.
⑵求出了的每一个取值的概率.
⑵ .
⑴.
探究新知
概率分布还经常用图象来表示
O
1 2 3 4 5 6 7 8
p
0.1
0.2
1、离散型随机变量的分布列完全描述了由这个随机变量所刻画的随机现象.
2、函数可以用解析式、表格或图象表示,离散型随机变量可以用分布列、等式或图象来表示.
可以看出的取值范围是{1,2,3,4,5,6},它取每一个值的概率都是
典例讲解
例1、设随机变量X的分布列为,求:
(1)或;
(2).
(1)∵
∴,
则或
.
解析
典例讲解
例1、设随机变量X的分布列为,求:
(1)或;
(2).
(2)由,
可得
.
解析
方法归纳
利用分布列及其性质解题时要注意以下两个问题:
(1)的各个取值表示的事件是互斥的.
(2)不仅要注意 ,而且要注意.
变式训练
1.若离散型随机变量的分布列为:
求常数及相应的分布列.
由分布列的性质可知:,即,解得或,又因,即,故.所以,此时,.所以随机变量的分布列为:
解析
0 1
典例讲解
随机变量的可能取值为3,4,5,6.
从袋中随机取3个球,包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为,事件“”包含的基本事件总数为.
从而有
,
例2.口袋中有6个同样大小的黑球,编号为1,2,3,4,5,6,现从中随机取出3个球,用表示取出的最大号码,求的分布列.
解析
典例讲解
,
所以随机变量的分布列为
例2.口袋中有6个同样大小的黑球,编号为1,2,3,4,5,6,现从中随机取出3个球,用表示取出的最大号码,求的分布列.
解析
X 3 4 5 6
P
方法归纳
1.求离散型随机变量的分布列的步骤
(1)找出随机变量的所有可能的取值.
(2)求出取每一个值的概率.
(3)列出表格.
2.求离散型随机变量分布列时应注意的问题
(1)确定离散型随机变量的分布列的关键是要搞清取每一个值对应的随机事件,进一步利用排列、组合知识求出取每一个值的概率.对于随机变量取值较多时,应由简单情况先导出一般的通式,从而简化过程.
(2)在求离散型随机变量的分布列时,要充分利用分布列的性质,这样不但可以减少运算量,还可验证分布列是否正确.
变式训练
解析
2.从装有6个白球,4个黑球和2个黄球的箱中随机地取出两个球,规定每取出一个黑球赢2元,而每取出一个白球输1元,取出黄球无输赢,以表示赢得的钱数,随机变量可以取哪些值呢?求的分布列.
从箱中取两个球的情形有以下6种:
{2白},{1白1黄},{1白1黑},{2黄},{1黑1黄},{2黑}.
当取到2白时,结果输2元,随机变量;
当取到1白1黄时,输1元,随机变量;
当取到1白1黑时,随机变量;
当取到2黄时,;
当取到1黑1黄时,;
变式训练
解析
2.从装有6个白球,4个黑球和2个黄球的箱中随机地取出两个球,规定每取出一个黑球赢2元,而每取出一个白球输1元,取出黄球无输赢,以表示赢得的钱数,随机变量可以取哪些值呢?求的分布列.
当取到2黑时,.
则的可能取值为.
变式训练
解析
2.从装有6个白球,4个黑球和2个黄球的箱中随机地取出两个球,规定每取出一个黑球赢2元,而每取出一个白球输1元,取出黄球无输赢,以表示赢得的钱数,随机变量可以取哪些值呢?求的分布列.
从而得到X的分布列如下:
-2 -1 0 1 2 4
探究新知
1.利用随机变量研究一类问题,如抽取的奖券是否中奖,买回的一件产品是否为正品,新生婴儿的性别,投篮是否命中等,这些问题有什么共同点?
【提示】这些问题的共同点是随机试验只有两个可能的结果.定义一个随机变量,使其中一个结果对应于1,另一个结果对应于0,即得到服从二点分布的随机变量.
问题
一般地,如果随机变量的分布列能写成上述表格的形式,则称这个随机变量服从参数的两点分布(或0-1分布).
1 0
探究新知
2.只取两个不同值的随机变量是否一定服从二点分布?
【提示】不一定.如随机变量的分布列由下表给出
不服从二点分布,因为的取值不是0或1 .
2 5
0.3 0.7
典例讲解
例3.袋内有10个白球,5个红球,从中摸出2个球,记求的分布列.
由题设可知服从二点分布.
.
∴的分布列为
解析
0 1
方法归纳
1.看取值:随机变量只取两个值0和1.
2.验概率:检验是否成立.
如果一个分布满足以上两点,则该分布是二点分布,否则不是二点分布.
两步法判断一个分布是否为二点分布
变式训练
由离散型随机变量分布列的性质可知,,解得.
3.若离散型随机变量的分布列为
解析
则( )
A. B. C. D.
0 1
C
素养提炼
(1)离散型随机变量的分布列不仅能清楚地反映离散型随机变量的所有可能取值,而且能清楚地看到取每一个值的概率的大小,从而反映了离散型随机变量在随机试验中取值的分布情况
(2)由于离散型随机变量的各个取值之间彼此互斥,因此离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和
离散型随机变量的分布列
当堂练习
1.设是一个离散型随机变量,其分布列为
A
则常数的值为( )
A. B. C.或 D. 或
0 1
由离散型随机变量分布列的性质可得
,,解得
解析
2.随机变量的分布列如下:
当堂练习
由分布列的性质得
,
解得.故.
解析
则________,________.
1 2 3 4 5 6
0.2 0.35 0.1 0.15 0.2
当堂练习
3.在学校组织的足球比赛中,某班要与其他4个班级各赛一场,在这4场比赛的任意一场中,此班级每次胜、负、平的概率相等.已知当这4场比赛结束后,该班胜场多于负场.
(1)求该班级胜场多于负场的所有可能的个数和;
(2)若胜场次数为,求的分布列.
解析
(1)若胜一场,则其余为平,共有种情况;若胜两场,则其余两场为一负一平或两平,共有种情况;若胜三场,则其余一场为负或平,共有种情况;若胜四场,则只有一种情况.综上,共有31种情况.
当堂练习
3.在学校组织的足球比赛中,某班要与其他4个班级各赛一场,在这4场比赛的任意一场中,此班级每次胜、负、平的概率相等.已知当这4场比赛结束后,该班胜场多于负场.
(1)求该班级胜场多于负场的所有可能的个数和;
(2)若胜场次数为,求的分布列.
解析
(2) 的可能取值为1,2,3,4,
所以的分布列为
1 2 3 4
归纳小结
离散型随机变量的分布列
特殊分布
定义
性质
求法
二点分布
作 业
课本P60页练习:3,4
