人教A版(2019)高中数学选择性必修第三册7.3.2 《离散型随机变量的方差》教学设计
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册7.3.2 《离散型随机变量的方差》教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览



文档简介
《离散型随机变量的方差》教学设计
一、导语
随机变量的均值是一个重要的数字特征,它反映了随机变量取值的平均水平或分布的“集中趋势”.因为随机变量的取值围绕其均值波动,而随机变量的均值无法反映波动幅度的大小,所以我们还需要寻找反映随机变量取值波动大小的数字特征.
设计意图:通过谈话,引入课题.
二、探究新知
探究1:从两名同学中挑出一名代表班级参加射击比赛.根据以往的成绩记录,甲、乙两名同学击中目标靶的环数X和Y的分布列如表1和表2所示.
如何评价这两名同学的射击水平
师生活动:教师提出探究问题,引导学生分析.
师:能不能用我们上一节课学习的均值分析这一问题 同学们尝试一下.
学生运算求解,求出甲、乙两名同学击中目标靶的环数的均值.
通过计算可得,.因为两个均值相等,所以根据均值不能区分这两名同学的射击水平.
追问1:平均水平相同,是不是这两名同学的射击水平就没有差距呢 我们还能不能从其他角度进一步考察这两名同学的射击水平呢
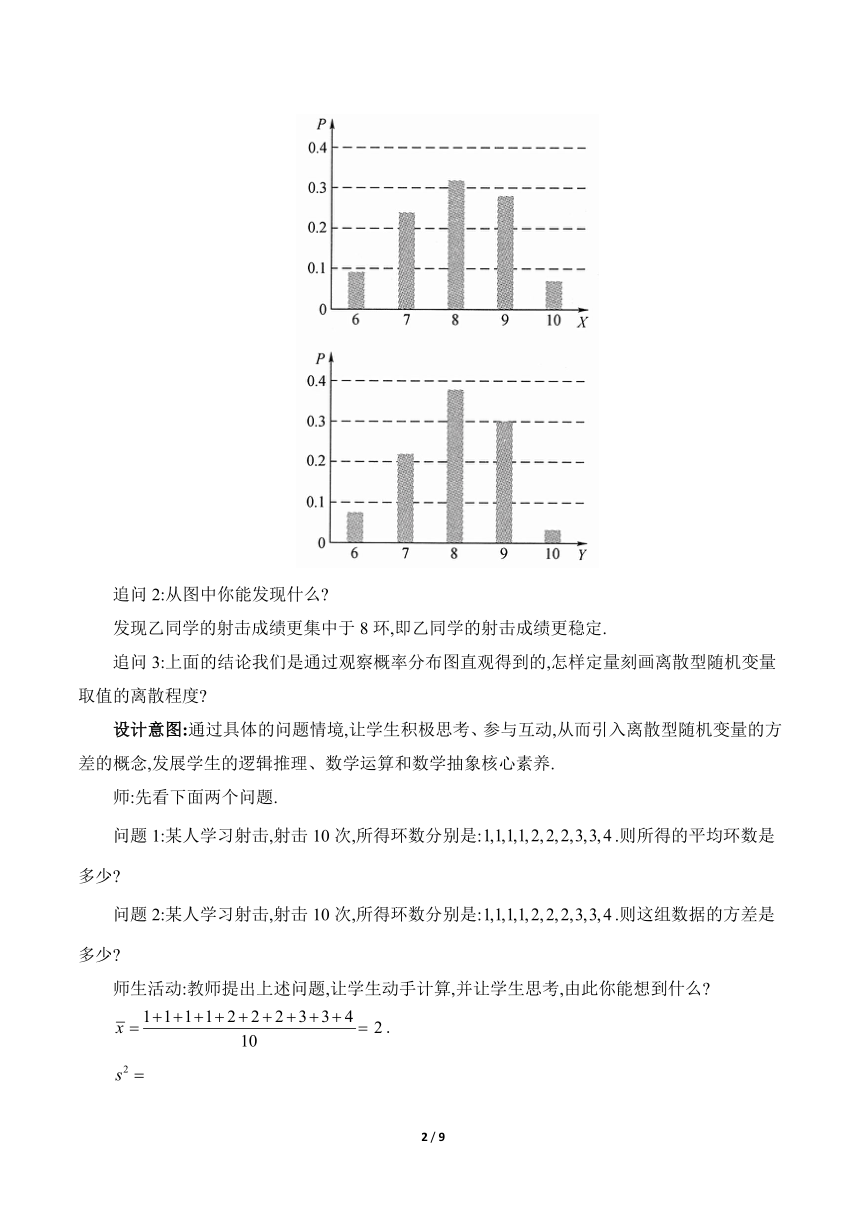
下面我们从稳定性的角度考虑,你能根据表1和表2画出这两名同学击中环数的概率分布图吗 同学们动手试一下.
学生尝试独立完成,教师出示下图.
追问2:从图中你能发现什么
发现乙同学的射击成绩更集中于8环,即乙同学的射击成绩更稳定.
追问3:上面的结论我们是通过观察概率分布图直观得到的,怎样定量刻画离散型随机变量取值的离散程度
设计意图:通过具体的问题情境,让学生积极思考、参与互动,从而引入离散型随机变量的方差的概念,发展学生的逻辑推理、数学运算和数学抽象核心素养.
师:先看下面两个问题.
问题1:某人学习射击,射击10次,所得环数分别是:.则所得的平均环数是多少
问题2:某人学习射击,射击10次,所得环数分别是:.则这组数据的方差是多少
师生活动:教师提出上述问题,让学生动手计算,并让学生思考,由此你能想到什么
.
.
设计意图:通过问题1、问题2,为引入离散型随机变量的方差的概念作准备.
教师提问:我们知道,样本方差可以度量一组样本数据的离散程度,它是通过计算所有数据与样本均值的“偏差平方的平均值”来实现的.一个自然的想法是,随机变量的离散程度能否用可能取值与均值的“偏差平方的平均值”来度量呢
学生讨论,得出:可以用偏差平方关于取值概率的加权平均,来度量随机变量取值与其均值的偏离程度.
师生总结得出概念:
一般地,若离散型随机变量的分布列如下:
则称为随机变量的方差,有时也记为.
称为随机变量的标准差,记为.
说明:随机变量的方差和标准差都可以度量随机变量的取值与其均值的偏离程度,反映了随机变量取值的离散程度.方差或标准差越小,随机变量的取值越集中;方差或标准差越大,随机变量的取值越分散.
设计意图:让学生经历离散型随机变量的方差概念的建构过程,进一步体会从特殊到一般的思想,培养学生归纳、类比等合情推理的能力,提升数学抽象、逻辑推理等核心素养.
因此,探究1中,可以用两名同学射击成绩的方差和标准差来刻画他们射击成绩的稳定性.两名同学射击成绩的方差和标准差分别为
;
.
因为(等价地,),所以随机变量的取值相对更集中,即乙同学的射击成绩相对更稳定.
设计意图:让学生利用方差和标准差的定义求解探究1提出的问题,学以致用,提高学生的应用意识.
问题3:方差的计算可以简化吗
教师提出问题,先让学生思考,再出示简化的结果.
.
让学生区分与.
设计意图:有助于学生更好地理解方差的本质.
探究2:离散型随机变量加上一个常数,方差会有怎样变化 离散型随机变量乘一个常数,方差又有怎样的变化 它们和期望的性质有什么不同
师生活动:教师提出问题,让学生充分思考、讨论、交流.在此基础上,找几名学生代表分享讨论交流的结果.
学生发言后,教师进行评价指导,最后共同得出结论.
离散型随机变量加上一个常数,其均值也相应加上常数,故不改变与其均值的离散程度,方差保持不变,即.而离散型随机变量乘一个常数,其方差变为原方差的倍,即.因此,.
用定义证明(供教师参考):
设离散型随机变量的分布列为
由(为常数)知也是离散型随机变量.的分布列为
由均值的性质得,于是
.
设计意图:类比均值的性质,推导得出方差的性质.根据学生的情况,教师可以引导学生用方差的定义证明这一结论,提高学生的逻辑推理核心素养.
三、典例剖析
例1 抛郑一枚质地均匀的骰子,求掷出的点数的方差.
师生活动:教师让学生利用方差的定义进行计算.集体核对.
解:随机变量的分布列为,
因为,
所以.
教师指出:方差的计算需要一定的运算能力,在随机变量的均值比较容易计算的情况下,运用公式不失为一种比较实用的方法.另外注意方差性质的应用,即.
设计意图:通过例题,提升对概念精细化的理解.让学生掌握方差的算法,发展学生的逻辑推理、直观想象、数学抽象和数学运算核心素养.
例2 投资两种股票,每股收益的分布列分别如表1和表2所示.
(1)投资哪种股票的期望收益大
(2)投资哪种股票的风险较高
师生活动:
教师提问:你能用我们所学的知识分析、解决这一生活中的实际问题吗
教师可以引导分析第(2)问,我们如何衡量投资风险的高低
解:(1)股票和股票投资收益的期望分别为
,
.
因为,所以投资股票的期望收益较大.
(2)股票和股票投资收益的方差分别为
,
因为和相差不大,且,所以投资股票比投资股票的风险高.
设计意图:例2是综合利用均值和方差比较投资两种股票收益的问题,目的是使学生了解在实际问题中均值和方差的意义.在这个问题中,均值表示平均收益,方差表示风险(不确定性).在教学中,可以提供更多不同背景的实际问题,帮助学生了解均值、方差的意义.
师生共同归纳总结利用均值和方差的意义解决实际问题的步骤:
(1)比较均值.离散型随机变量的均值反映了离散型随机变量取值的平均水平,因此,在实际决策问题中,需先计算均值,看一下谁的平均水平高.
(2)在均值相等或接近的情况下计算方差.方差反映了离散型随机变量取值的稳定与波动、集中与离散的程度.通过计算方差,分析一下谁的水平发挥相对稳定.
(3)下结论.依据均值和方差给出结论.
四、达标检测
1.把随机变量X的分布列填写完整,并完成填空.
若,则______,______.
2.已知离散型随机变量的分布列如下.若,则______,______,______.
3.甲、乙两个野生动物保护区有相同的自然环境,且野生动物的种类和数量也大致相等,而两个保护区内每个季度发生的违规事件次数的分布列分别如下.
甲保护区:
乙保护区:
试计算这两个保护区每个季度发生的违规事件次数的均值和方差.
答案
1. (点拨:由分布列的性质知,分布列中应填..)
2. (点拨:由题知,解得,.)
3.甲保护区违规事件次数的均值和方差分别为
,
.
乙保护区违规事件次数的均值和方差分别为
,
.
设计意图:通过练习,巩固本节所学知识.通过学生解决问题,发展学生的数学运算、数学建模核心素养.
五、课堂总结
1.离散型随机变量的方差是如何定义的 我们是如何得出随机变量方差公式的
2.在计算离散型随机变量的方差时,我们如何选择公式简化运算
3.如何利用方差和标准差分析、解决生活中的实际问题
设计意图:通过总结,让学生进一步巩固本节所学内容,提高概括能力.
六、布置作业
教材第70页练习第题.
板书设计:
7.3.2离散型随机变量的方差 1.一般地,若离散型随机变量的分布列如下: 则称为随机变量的方差,有时也记为 2.称为随机变量的标准差,记为 3.离散型随机变量方差的性质 4.例题 例1 例2
1 / 9
一、导语
随机变量的均值是一个重要的数字特征,它反映了随机变量取值的平均水平或分布的“集中趋势”.因为随机变量的取值围绕其均值波动,而随机变量的均值无法反映波动幅度的大小,所以我们还需要寻找反映随机变量取值波动大小的数字特征.
设计意图:通过谈话,引入课题.
二、探究新知
探究1:从两名同学中挑出一名代表班级参加射击比赛.根据以往的成绩记录,甲、乙两名同学击中目标靶的环数X和Y的分布列如表1和表2所示.
如何评价这两名同学的射击水平
师生活动:教师提出探究问题,引导学生分析.
师:能不能用我们上一节课学习的均值分析这一问题 同学们尝试一下.
学生运算求解,求出甲、乙两名同学击中目标靶的环数的均值.
通过计算可得,.因为两个均值相等,所以根据均值不能区分这两名同学的射击水平.
追问1:平均水平相同,是不是这两名同学的射击水平就没有差距呢 我们还能不能从其他角度进一步考察这两名同学的射击水平呢
下面我们从稳定性的角度考虑,你能根据表1和表2画出这两名同学击中环数的概率分布图吗 同学们动手试一下.
学生尝试独立完成,教师出示下图.
追问2:从图中你能发现什么
发现乙同学的射击成绩更集中于8环,即乙同学的射击成绩更稳定.
追问3:上面的结论我们是通过观察概率分布图直观得到的,怎样定量刻画离散型随机变量取值的离散程度
设计意图:通过具体的问题情境,让学生积极思考、参与互动,从而引入离散型随机变量的方差的概念,发展学生的逻辑推理、数学运算和数学抽象核心素养.
师:先看下面两个问题.
问题1:某人学习射击,射击10次,所得环数分别是:.则所得的平均环数是多少
问题2:某人学习射击,射击10次,所得环数分别是:.则这组数据的方差是多少
师生活动:教师提出上述问题,让学生动手计算,并让学生思考,由此你能想到什么
.
.
设计意图:通过问题1、问题2,为引入离散型随机变量的方差的概念作准备.
教师提问:我们知道,样本方差可以度量一组样本数据的离散程度,它是通过计算所有数据与样本均值的“偏差平方的平均值”来实现的.一个自然的想法是,随机变量的离散程度能否用可能取值与均值的“偏差平方的平均值”来度量呢
学生讨论,得出:可以用偏差平方关于取值概率的加权平均,来度量随机变量取值与其均值的偏离程度.
师生总结得出概念:
一般地,若离散型随机变量的分布列如下:
则称为随机变量的方差,有时也记为.
称为随机变量的标准差,记为.
说明:随机变量的方差和标准差都可以度量随机变量的取值与其均值的偏离程度,反映了随机变量取值的离散程度.方差或标准差越小,随机变量的取值越集中;方差或标准差越大,随机变量的取值越分散.
设计意图:让学生经历离散型随机变量的方差概念的建构过程,进一步体会从特殊到一般的思想,培养学生归纳、类比等合情推理的能力,提升数学抽象、逻辑推理等核心素养.
因此,探究1中,可以用两名同学射击成绩的方差和标准差来刻画他们射击成绩的稳定性.两名同学射击成绩的方差和标准差分别为
;
.
因为(等价地,),所以随机变量的取值相对更集中,即乙同学的射击成绩相对更稳定.
设计意图:让学生利用方差和标准差的定义求解探究1提出的问题,学以致用,提高学生的应用意识.
问题3:方差的计算可以简化吗
教师提出问题,先让学生思考,再出示简化的结果.
.
让学生区分与.
设计意图:有助于学生更好地理解方差的本质.
探究2:离散型随机变量加上一个常数,方差会有怎样变化 离散型随机变量乘一个常数,方差又有怎样的变化 它们和期望的性质有什么不同
师生活动:教师提出问题,让学生充分思考、讨论、交流.在此基础上,找几名学生代表分享讨论交流的结果.
学生发言后,教师进行评价指导,最后共同得出结论.
离散型随机变量加上一个常数,其均值也相应加上常数,故不改变与其均值的离散程度,方差保持不变,即.而离散型随机变量乘一个常数,其方差变为原方差的倍,即.因此,.
用定义证明(供教师参考):
设离散型随机变量的分布列为
由(为常数)知也是离散型随机变量.的分布列为
由均值的性质得,于是
.
设计意图:类比均值的性质,推导得出方差的性质.根据学生的情况,教师可以引导学生用方差的定义证明这一结论,提高学生的逻辑推理核心素养.
三、典例剖析
例1 抛郑一枚质地均匀的骰子,求掷出的点数的方差.
师生活动:教师让学生利用方差的定义进行计算.集体核对.
解:随机变量的分布列为,
因为,
所以.
教师指出:方差的计算需要一定的运算能力,在随机变量的均值比较容易计算的情况下,运用公式不失为一种比较实用的方法.另外注意方差性质的应用,即.
设计意图:通过例题,提升对概念精细化的理解.让学生掌握方差的算法,发展学生的逻辑推理、直观想象、数学抽象和数学运算核心素养.
例2 投资两种股票,每股收益的分布列分别如表1和表2所示.
(1)投资哪种股票的期望收益大
(2)投资哪种股票的风险较高
师生活动:
教师提问:你能用我们所学的知识分析、解决这一生活中的实际问题吗
教师可以引导分析第(2)问,我们如何衡量投资风险的高低
解:(1)股票和股票投资收益的期望分别为
,
.
因为,所以投资股票的期望收益较大.
(2)股票和股票投资收益的方差分别为
,
因为和相差不大,且,所以投资股票比投资股票的风险高.
设计意图:例2是综合利用均值和方差比较投资两种股票收益的问题,目的是使学生了解在实际问题中均值和方差的意义.在这个问题中,均值表示平均收益,方差表示风险(不确定性).在教学中,可以提供更多不同背景的实际问题,帮助学生了解均值、方差的意义.
师生共同归纳总结利用均值和方差的意义解决实际问题的步骤:
(1)比较均值.离散型随机变量的均值反映了离散型随机变量取值的平均水平,因此,在实际决策问题中,需先计算均值,看一下谁的平均水平高.
(2)在均值相等或接近的情况下计算方差.方差反映了离散型随机变量取值的稳定与波动、集中与离散的程度.通过计算方差,分析一下谁的水平发挥相对稳定.
(3)下结论.依据均值和方差给出结论.
四、达标检测
1.把随机变量X的分布列填写完整,并完成填空.
若,则______,______.
2.已知离散型随机变量的分布列如下.若,则______,______,______.
3.甲、乙两个野生动物保护区有相同的自然环境,且野生动物的种类和数量也大致相等,而两个保护区内每个季度发生的违规事件次数的分布列分别如下.
甲保护区:
乙保护区:
试计算这两个保护区每个季度发生的违规事件次数的均值和方差.
答案
1. (点拨:由分布列的性质知,分布列中应填..)
2. (点拨:由题知,解得,.)
3.甲保护区违规事件次数的均值和方差分别为
,
.
乙保护区违规事件次数的均值和方差分别为
,
.
设计意图:通过练习,巩固本节所学知识.通过学生解决问题,发展学生的数学运算、数学建模核心素养.
五、课堂总结
1.离散型随机变量的方差是如何定义的 我们是如何得出随机变量方差公式的
2.在计算离散型随机变量的方差时,我们如何选择公式简化运算
3.如何利用方差和标准差分析、解决生活中的实际问题
设计意图:通过总结,让学生进一步巩固本节所学内容,提高概括能力.
六、布置作业
教材第70页练习第题.
板书设计:
7.3.2离散型随机变量的方差 1.一般地,若离散型随机变量的分布列如下: 则称为随机变量的方差,有时也记为 2.称为随机变量的标准差,记为 3.离散型随机变量方差的性质 4.例题 例1 例2
1 / 9
