人教B版(2019)高中数学必修第一册1.1.3 集合的基本运算---第二课时补集及集合运算的综合 课件(共23张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学必修第一册1.1.3 集合的基本运算---第二课时补集及集合运算的综合 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 302.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 12:41:18 | ||
图片预览








文档简介
(共23张PPT)
1.1 集合
第一章 集合与常用逻辑用语
1.1.3 集合的基本运算
第二课时 补集及集合运算的综合
学习目标
1.理解交集、并集的概念,会用文字语言、符号语言及图形语言来描述这些概念,
2.了解交集、并集的一些简单性质,会求两个简单集合的并集与交集,
3.能借助Venn图来探讨集合之间的关系及运算规律,
4.在具体情境中,了解全集的含义,
5.理解在给定集合中一个子集的补集的含义,能求给定子集的补集.
学习目标
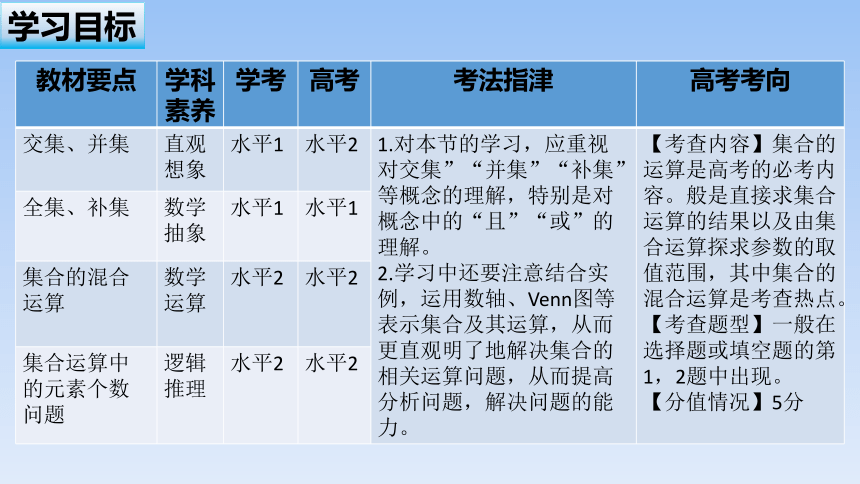
教材要点 学科素养 学考 高考 考法指津 高考考向
交集、并集 直观想象 水平1 水平2 1.对本节的学习,应重视对交集”“并集”“补集”等概念的理解,特别是对概念中的“且”“或”的理解。 2.学习中还要注意结合实例,运用数轴、Venn图等表示集合及其运算,从而更直观明了地解决集合的相关运算问题,从而提高分析问题,解决问题的能力。 【考查内容】集合的运算是高考的必考内容。般是直接求集合运算的结果以及由集合运算探求参数的取值范围,其中集合的混合运算是考查热点。【考查题型】一般在选择题或填空题的第1,2题中出现。
【分值情况】5分
全集、补集 数学抽象 水平1 水平1
集合的混合运算 数学运算 水平2 水平2
集合运算中的元素个数问题 逻辑推理 水平2 水平2
知识点一 全集与补集
(一)教材梳理填空
一、自学教材·注重基础
(1)全集:如果所要研究的集合都是某一给定集合的______,那么称_______________为全集,全集通常用U表示.
(2)补集:文字语言:如果集合A是全集U的一个子集,则由U中________的所有元素组成的集合,称为A在U中的补集,记作______
符号语言: UA={x|x∈U且x A}
图形语言:
运算性质: UA U, UU= , U =___,A∪( UA)=___,A∩( UA)= , U( UA)=____
不属于A
UA
U
U
A
(二)基本知能小试
1.判断正误
(1)全集一定含有任何元素. ( )
(2)集合 RA= QA. ( )
(3)一个集合的补集一定含有元素. ( )
(4)研究A在U中的补集时,A可以不是U的子集. ( )
x
一、自学教材·注重基础
2.已知全集U={-1,0,1},且 UA={0},则A=________.
解析: ∵U={-1,0,1}, UA={0},∴A={-1,1}.
{-1,1}
知识点一 全集与补集
x
x
x
(二)基本知能小试
一、自学教材·注重基础
知识点一 全集与补集
3.设全集为U,M={1,2}, UM={3},则U=________.
解析:U=M∪ UM={1,2}∪{3}={1,2,3}.
{1,2,3}
4.若集合A=(1,+∞),则 RA=___________.
解析:∵A=(1,+∞),∴ RA=(-∞,1].
(-∞,1]
题型一 补集的运算
二、提升新知·注重综合
(1)补集是相对于全集而言的,它与全集不可分割.一方面,若没有定义全集,则不存在补集的说法;另一方面,补集的元素逃不出全集的范围.
(2)补集既是集合之间的一种关系,同时也是集合之间的一种运算.求集合A的补集的前提是A为全集U的子集,随着所选全集的不同,得到的补集也是不同的.
(3)符号 UA有三层意思:
①A是U的子集,即A U;
② UA表示一个集合,且( UA) U;
③ UA是U中不属于A的所有元素组成的集合,即 UA={x|x∈U,且x A}.
(4)若x∈U,则x∈A或x∈ UA,二者必居其一.
[典例1] (1)设集合U={1,2,3,4,5,6},M={1,2,4},则 UM= ( )
A.U B.{1,3,5}
C.{3,5,6} D.{2,4,6}
(2)已知全集U=R,集合A={x|x<-2或x>2},则 UA=____________.
(1)因为U={1,2,3,4,5,6},M={1,2,4},所以由补集的定义,可知 UM={3,5,6}.
(2)如图,在数轴上表示出集合A,可知 UA={x|-2≤x≤2}.
C
解析
二、提升新知·注重综合
{x|-2≤x≤2}
题型一 补集的运算
方法总结
二、提升新知·注重综合
求集合补集的策略
(1)如果所给集合是有限集,则先把集合中的元素一一列举出来,然后结合补集的定义来求解.另外,针对此类问题,在解答过程中也常常借助Venn图来求解,这样处理相对来说比较直观、形象,且解答时不易出错.
(2)如果所给集合是无限集,在解答有关集合补集问题时,则常借助数轴,先把已知集合及全集分别表示在数轴上,然后根据补集的定义求解.
题型一 补集的运算
变式训练
1.若全集U=[-2,2],A=[-2,0],则 UA等于 ( )
A.(0,2) B.[0,2) C.(0,2] D.[0,2]
解析:∵U=[-2,2],A=[-2,0],
∴ UA=(0,2],故选C.
C
二、提升新知·注重综合
题型一 补集的运算
2.已知全集U={(x,y)|x∈R,y∈R},集合A={(x,y)|xy>0},则 UA=_____________.
解析:A={(x,y)|xy>0}表示平面直角坐标系中第一、三象限的点,其补集应为第二、四象限的点及坐标轴上的点.
{(x,y)|xy≤0}
变式训练
3.设全集S={1,2,3,4},且A={x∈S|x2-5x+m=0},若 SA={2,3},则m=________.
解析:因为S={1,2,3,4}, SA={2,3},所以A={1,4},即1,4是方程x2-5x+m=0的两根,由根与系数的关系可得m=1×4=4.
4
二、提升新知·注重综合
题型一 补集的运算
题型二 集合的交、并、补集的综合运算
二、提升新知·注重综合
例2、已知全集U={x|x≤4},集合A={x|-2<x<3},B={x|-3≤x≤2}.
(1)求A∩B,( UA)∪B,A∩( UB);
(2)求 U(A∪B)和 U(A∩B).
解析
(1)因为A={x|-2<x<3},B={x|-3≤x≤2},所以 UA={x|x≤-2或3≤x≤4},
UB={x|x<-3或2<x≤4},
所以A∩B={x|-2<x≤2},( UA)∪B={x|x≤2或3≤x≤4},A∩( UB)={x|2<x<3}.
(2)由条件知A∪B={x|-3≤x<3},所以 U(A∪B)={x|x<-3或3≤x≤4}.
又A∩B={x|-2<x≤2},所以 U(A∩B)={x|x≤-2或2<x≤4}.
方法总结
二、提升新知·注重综合
解决集合运算问题的方法
(1)要进行集合运算时,首先必须熟练掌握基本运算法则,可按照如下口诀进行:
交集元素仔细找,属于A且属于B;
并集元素勿遗漏,切忌重复仅取一;
全集U是大范围,去掉U中A元素,剩余元素成补集.
(2)解决集合的混合运算问题时,一般先运算括号内的部分,如求( UA)∩B时,先求出 UA,再求交集;求 U(A∪B)时,先求出A∪B,再求补集.
(3)当集合是用列举法表示时(如数集),可以通过列举集合的元素分别得到所求的集合;当集合是用描述法表示时(如不等式形式表示的集合),则可运用数轴求解.
题型二 集合的交、并、补集的综合运算
变式训练
二、提升新知·注重综合
1.设全集U={1,2,3,4,5,6,7,8},M={1,3,5,7},N={5,6,7},则 U(M∪N)= ( )
A.{5,7} B.{2,4} C.{2,4,8} D.{1,3,5,6,7}
解析:∵M∪N={1,3,5,7}∪{5,6,7}={1,3,5,6,7},∴ U(M∪N)={2,4,8}.
C
题型二 集合的交、并、补集的综合运算
2.设全集U=M∪N={1,2,3,4,5},M∩( UN)={2,4},则N= ( )
A.{1,2,3} B.{1,3,5} C.{1,4,5} D.{2,3,4}
B
解析:画出Venn图,阴影部分为M∩( UN)={2,4},所以N={1,3,5}.
变式训练
二、提升新知·注重综合
3.已知全集U=R,集合A={x|x+1<0},B={x|x-3<0},那么集合( UA)∩B= ( )
A.{x|-1≤x<3} B.{x|-1<x<3}
C.{x|x<-1} D.{x|x>3}
解析:∵A={x|x+1<0}={x|x<-1},B={x|x-3<0}={x|x<3},∴ UA={x|x≥-1},
∴( UA)∩B={x|-1≤x<3}.
A
题型二 集合的交、并、补集的综合运算
例3、设集合A={x|x+m≥0},B={x|-2题型三 与补集有关的求参数问题
由已知A={x|x≥-m},
得 UA={x|x<-m},
因为B={x|-2解析
二、提升新知·注重综合
所以-m≤-2,即m≥2,
所以m的取值范围是[2,+∞).
方法总结
二、提升新知·注重综合
由集合的补集求解参数的问题
(1)如果所给集合是有限集,由补集求参数问题时,可利用补集定义并结合知识求解.
(2)如果所给集合是无限集,与集合交、并、补运算有关的求参数问题时,一般利用数轴分析法求解.
题型三 与补集有关的求参数问题
变式训练
二、提升新知·注重综合
例3、设集合A={x|x+m≥0},B={x|-21.[变条件]本例将条件“( UA)∩B= ”改为“( UA)∩B≠ ”,其他条件不变,则m的取值范围又是什么?
解析:由已知得A={x|x≥-m},
所以 UA={x|x<-m},
又( UA)∩B≠ ,
所以-m>-2,解得m<2.
题型三 与补集有关的求参数问题
变式训练
二、提升新知·注重综合
例3、设集合A={x|x+m≥0},B={x|-22.[变条件]本例将条件“( UA)∩B= ”改为“( UB)∪A=R”,其他条件不变,则m的取值范围又是什么?
解析:由已知A={x|x≥-m}, UB={x|x≤-2或x≥4}.
又( UB)∪A=R,
所以-m≤-2,解得m≥2.
题型三 与补集有关的求参数问题
变式训练
二、提升新知·注重综合
3.已知集合A={x|-2<x<3},B={x|m<x<m+9},若( RA)∩B=B.求实数m的取值范围.
解析: RA={x|x≤-2或x≥3},由( RA)∩B=B,得B RA,∴m+9≤-2或m≥3,解得m≤-11或m≥3,故m的取值范围是(-∞,-11]∪[3,+∞).
题型三 与补集有关的求参数问题
当堂练习
1.设集合U={1,2,3,4,5},A={1,2,3},B={2,3,4},则 U(A∩B)等于 ( )
A.{2,3} B.{1,4,5} C.{4,5} D.{1,5}
一、基础经典题
解析:∵A∩B={2,3},∴ U(A∩B)={1,4,5}.
B
2.设全集U={x|x≥0},集合P={1},则 UP等于 ( )
A.{x|0≤x<1或x>1} B.{x|x<1}
C.{x|x<1或x>1} D.{x|x>1}
解析:因为U={x|x≥0},P={1},
所以 UP={x|x≥0且x≠1}={x|0≤x<1或x>1}.
A
三、训练素养·注重应用、创新
当堂练习
3.设全集U=R,集合A={x|0≤x≤2},B={y|1≤y≤3},则( UA)∪B=_____________.
解析:因为 UA={x|x>2或x<0},B={y|1≤y≤3},所以( UA)∪B={x|x<0或x≥1}.
4.已知全集U=R,M={x|-1解析:∵U=R, UN={x|0∴N={x|x≤0或x≥2},
∴M∪N={x|-1={x|x<1或x≥2}.
{x|x<0或x≥1}
三、训练素养·注重应用、创新
当堂练习
5.已知全集U={小于10的正整数},A U,B U,且( UA)∩B={1,8},A∩B={2,3},( UA)∩( UB)={4,6,9}.
(1)求集合A与B;
(2)求( RU)∪[ Z(A∩B)](其中R为实数集,Z为整数集).
解析:由( UA)∩B={1,8},知1∈B,8∈B;由( UA)∩( UB)={4,6,9},知4,6,9 A,且4,6,9 B;由A∩B={2,3},知2,3是集合A与B的公共元素.
因为U={1,2,3,4,5,6,7,8,9},所以5,7∈A.画出Venn图,如图所示.
(1)由图可知A={2,3,5,7},B={1,2,3,8}.
二、创新应用题
三、训练素养·注重应用、创新
1.1 集合
第一章 集合与常用逻辑用语
1.1.3 集合的基本运算
第二课时 补集及集合运算的综合
学习目标
1.理解交集、并集的概念,会用文字语言、符号语言及图形语言来描述这些概念,
2.了解交集、并集的一些简单性质,会求两个简单集合的并集与交集,
3.能借助Venn图来探讨集合之间的关系及运算规律,
4.在具体情境中,了解全集的含义,
5.理解在给定集合中一个子集的补集的含义,能求给定子集的补集.
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
交集、并集 直观想象 水平1 水平2 1.对本节的学习,应重视对交集”“并集”“补集”等概念的理解,特别是对概念中的“且”“或”的理解。 2.学习中还要注意结合实例,运用数轴、Venn图等表示集合及其运算,从而更直观明了地解决集合的相关运算问题,从而提高分析问题,解决问题的能力。 【考查内容】集合的运算是高考的必考内容。般是直接求集合运算的结果以及由集合运算探求参数的取值范围,其中集合的混合运算是考查热点。【考查题型】一般在选择题或填空题的第1,2题中出现。
【分值情况】5分
全集、补集 数学抽象 水平1 水平1
集合的混合运算 数学运算 水平2 水平2
集合运算中的元素个数问题 逻辑推理 水平2 水平2
知识点一 全集与补集
(一)教材梳理填空
一、自学教材·注重基础
(1)全集:如果所要研究的集合都是某一给定集合的______,那么称_______________为全集,全集通常用U表示.
(2)补集:文字语言:如果集合A是全集U的一个子集,则由U中________的所有元素组成的集合,称为A在U中的补集,记作______
符号语言: UA={x|x∈U且x A}
图形语言:
运算性质: UA U, UU= , U =___,A∪( UA)=___,A∩( UA)= , U( UA)=____
不属于A
UA
U
U
A
(二)基本知能小试
1.判断正误
(1)全集一定含有任何元素. ( )
(2)集合 RA= QA. ( )
(3)一个集合的补集一定含有元素. ( )
(4)研究A在U中的补集时,A可以不是U的子集. ( )
x
一、自学教材·注重基础
2.已知全集U={-1,0,1},且 UA={0},则A=________.
解析: ∵U={-1,0,1}, UA={0},∴A={-1,1}.
{-1,1}
知识点一 全集与补集
x
x
x
(二)基本知能小试
一、自学教材·注重基础
知识点一 全集与补集
3.设全集为U,M={1,2}, UM={3},则U=________.
解析:U=M∪ UM={1,2}∪{3}={1,2,3}.
{1,2,3}
4.若集合A=(1,+∞),则 RA=___________.
解析:∵A=(1,+∞),∴ RA=(-∞,1].
(-∞,1]
题型一 补集的运算
二、提升新知·注重综合
(1)补集是相对于全集而言的,它与全集不可分割.一方面,若没有定义全集,则不存在补集的说法;另一方面,补集的元素逃不出全集的范围.
(2)补集既是集合之间的一种关系,同时也是集合之间的一种运算.求集合A的补集的前提是A为全集U的子集,随着所选全集的不同,得到的补集也是不同的.
(3)符号 UA有三层意思:
①A是U的子集,即A U;
② UA表示一个集合,且( UA) U;
③ UA是U中不属于A的所有元素组成的集合,即 UA={x|x∈U,且x A}.
(4)若x∈U,则x∈A或x∈ UA,二者必居其一.
[典例1] (1)设集合U={1,2,3,4,5,6},M={1,2,4},则 UM= ( )
A.U B.{1,3,5}
C.{3,5,6} D.{2,4,6}
(2)已知全集U=R,集合A={x|x<-2或x>2},则 UA=____________.
(1)因为U={1,2,3,4,5,6},M={1,2,4},所以由补集的定义,可知 UM={3,5,6}.
(2)如图,在数轴上表示出集合A,可知 UA={x|-2≤x≤2}.
C
解析
二、提升新知·注重综合
{x|-2≤x≤2}
题型一 补集的运算
方法总结
二、提升新知·注重综合
求集合补集的策略
(1)如果所给集合是有限集,则先把集合中的元素一一列举出来,然后结合补集的定义来求解.另外,针对此类问题,在解答过程中也常常借助Venn图来求解,这样处理相对来说比较直观、形象,且解答时不易出错.
(2)如果所给集合是无限集,在解答有关集合补集问题时,则常借助数轴,先把已知集合及全集分别表示在数轴上,然后根据补集的定义求解.
题型一 补集的运算
变式训练
1.若全集U=[-2,2],A=[-2,0],则 UA等于 ( )
A.(0,2) B.[0,2) C.(0,2] D.[0,2]
解析:∵U=[-2,2],A=[-2,0],
∴ UA=(0,2],故选C.
C
二、提升新知·注重综合
题型一 补集的运算
2.已知全集U={(x,y)|x∈R,y∈R},集合A={(x,y)|xy>0},则 UA=_____________.
解析:A={(x,y)|xy>0}表示平面直角坐标系中第一、三象限的点,其补集应为第二、四象限的点及坐标轴上的点.
{(x,y)|xy≤0}
变式训练
3.设全集S={1,2,3,4},且A={x∈S|x2-5x+m=0},若 SA={2,3},则m=________.
解析:因为S={1,2,3,4}, SA={2,3},所以A={1,4},即1,4是方程x2-5x+m=0的两根,由根与系数的关系可得m=1×4=4.
4
二、提升新知·注重综合
题型一 补集的运算
题型二 集合的交、并、补集的综合运算
二、提升新知·注重综合
例2、已知全集U={x|x≤4},集合A={x|-2<x<3},B={x|-3≤x≤2}.
(1)求A∩B,( UA)∪B,A∩( UB);
(2)求 U(A∪B)和 U(A∩B).
解析
(1)因为A={x|-2<x<3},B={x|-3≤x≤2},所以 UA={x|x≤-2或3≤x≤4},
UB={x|x<-3或2<x≤4},
所以A∩B={x|-2<x≤2},( UA)∪B={x|x≤2或3≤x≤4},A∩( UB)={x|2<x<3}.
(2)由条件知A∪B={x|-3≤x<3},所以 U(A∪B)={x|x<-3或3≤x≤4}.
又A∩B={x|-2<x≤2},所以 U(A∩B)={x|x≤-2或2<x≤4}.
方法总结
二、提升新知·注重综合
解决集合运算问题的方法
(1)要进行集合运算时,首先必须熟练掌握基本运算法则,可按照如下口诀进行:
交集元素仔细找,属于A且属于B;
并集元素勿遗漏,切忌重复仅取一;
全集U是大范围,去掉U中A元素,剩余元素成补集.
(2)解决集合的混合运算问题时,一般先运算括号内的部分,如求( UA)∩B时,先求出 UA,再求交集;求 U(A∪B)时,先求出A∪B,再求补集.
(3)当集合是用列举法表示时(如数集),可以通过列举集合的元素分别得到所求的集合;当集合是用描述法表示时(如不等式形式表示的集合),则可运用数轴求解.
题型二 集合的交、并、补集的综合运算
变式训练
二、提升新知·注重综合
1.设全集U={1,2,3,4,5,6,7,8},M={1,3,5,7},N={5,6,7},则 U(M∪N)= ( )
A.{5,7} B.{2,4} C.{2,4,8} D.{1,3,5,6,7}
解析:∵M∪N={1,3,5,7}∪{5,6,7}={1,3,5,6,7},∴ U(M∪N)={2,4,8}.
C
题型二 集合的交、并、补集的综合运算
2.设全集U=M∪N={1,2,3,4,5},M∩( UN)={2,4},则N= ( )
A.{1,2,3} B.{1,3,5} C.{1,4,5} D.{2,3,4}
B
解析:画出Venn图,阴影部分为M∩( UN)={2,4},所以N={1,3,5}.
变式训练
二、提升新知·注重综合
3.已知全集U=R,集合A={x|x+1<0},B={x|x-3<0},那么集合( UA)∩B= ( )
A.{x|-1≤x<3} B.{x|-1<x<3}
C.{x|x<-1} D.{x|x>3}
解析:∵A={x|x+1<0}={x|x<-1},B={x|x-3<0}={x|x<3},∴ UA={x|x≥-1},
∴( UA)∩B={x|-1≤x<3}.
A
题型二 集合的交、并、补集的综合运算
例3、设集合A={x|x+m≥0},B={x|-2
由已知A={x|x≥-m},
得 UA={x|x<-m},
因为B={x|-2
二、提升新知·注重综合
所以-m≤-2,即m≥2,
所以m的取值范围是[2,+∞).
方法总结
二、提升新知·注重综合
由集合的补集求解参数的问题
(1)如果所给集合是有限集,由补集求参数问题时,可利用补集定义并结合知识求解.
(2)如果所给集合是无限集,与集合交、并、补运算有关的求参数问题时,一般利用数轴分析法求解.
题型三 与补集有关的求参数问题
变式训练
二、提升新知·注重综合
例3、设集合A={x|x+m≥0},B={x|-2
解析:由已知得A={x|x≥-m},
所以 UA={x|x<-m},
又( UA)∩B≠ ,
所以-m>-2,解得m<2.
题型三 与补集有关的求参数问题
变式训练
二、提升新知·注重综合
例3、设集合A={x|x+m≥0},B={x|-2
解析:由已知A={x|x≥-m}, UB={x|x≤-2或x≥4}.
又( UB)∪A=R,
所以-m≤-2,解得m≥2.
题型三 与补集有关的求参数问题
变式训练
二、提升新知·注重综合
3.已知集合A={x|-2<x<3},B={x|m<x<m+9},若( RA)∩B=B.求实数m的取值范围.
解析: RA={x|x≤-2或x≥3},由( RA)∩B=B,得B RA,∴m+9≤-2或m≥3,解得m≤-11或m≥3,故m的取值范围是(-∞,-11]∪[3,+∞).
题型三 与补集有关的求参数问题
当堂练习
1.设集合U={1,2,3,4,5},A={1,2,3},B={2,3,4},则 U(A∩B)等于 ( )
A.{2,3} B.{1,4,5} C.{4,5} D.{1,5}
一、基础经典题
解析:∵A∩B={2,3},∴ U(A∩B)={1,4,5}.
B
2.设全集U={x|x≥0},集合P={1},则 UP等于 ( )
A.{x|0≤x<1或x>1} B.{x|x<1}
C.{x|x<1或x>1} D.{x|x>1}
解析:因为U={x|x≥0},P={1},
所以 UP={x|x≥0且x≠1}={x|0≤x<1或x>1}.
A
三、训练素养·注重应用、创新
当堂练习
3.设全集U=R,集合A={x|0≤x≤2},B={y|1≤y≤3},则( UA)∪B=_____________.
解析:因为 UA={x|x>2或x<0},B={y|1≤y≤3},所以( UA)∪B={x|x<0或x≥1}.
4.已知全集U=R,M={x|-1
∴M∪N={x|-1
{x|x<0或x≥1}
三、训练素养·注重应用、创新
当堂练习
5.已知全集U={小于10的正整数},A U,B U,且( UA)∩B={1,8},A∩B={2,3},( UA)∩( UB)={4,6,9}.
(1)求集合A与B;
(2)求( RU)∪[ Z(A∩B)](其中R为实数集,Z为整数集).
解析:由( UA)∩B={1,8},知1∈B,8∈B;由( UA)∩( UB)={4,6,9},知4,6,9 A,且4,6,9 B;由A∩B={2,3},知2,3是集合A与B的公共元素.
因为U={1,2,3,4,5,6,7,8,9},所以5,7∈A.画出Venn图,如图所示.
(1)由图可知A={2,3,5,7},B={1,2,3,8}.
二、创新应用题
三、训练素养·注重应用、创新
