人教B版(2019)高中数学必修第一册 1.1.3《集合的基本运算》教学设计二
文档属性
| 名称 | 人教B版(2019)高中数学必修第一册 1.1.3《集合的基本运算》教学设计二 |

|
|
| 格式 | docx | ||
| 文件大小 | 471.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览

文档简介
《集合的基本运算》教学设计
教学设计
一、阅读引导
1.阅读教材,问题导入.
阅读教材第14~19页内容,回答下列问题.
考察下列各个集合,你能说出集合与集合,之间的关系吗?
①,,;
②,,;
③,,.
提示:集合与集合,之间的关系是:
①;
②;
③设全集,则.
2.归纳总结,核心必记.
(1)一般地,给定两个集合,,由既属于又属于的所有元素(即和的公共元素)组成的集合,称为与的交集,记作,读作“交”,图示为:
(2)一般地,给定两个集合,,由这两个集合的所有元素组成的集合,称为与的并集,记作,读作“并”,图示为(1)或(2):
(3)如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,全集通常用表示.如果集合是全集的一个子集,则由中不属于的所有元素组成的集合,称为在中的补集,记作,读作“在中的补集”,图示为:
二、知识深化
1.集合的运算.
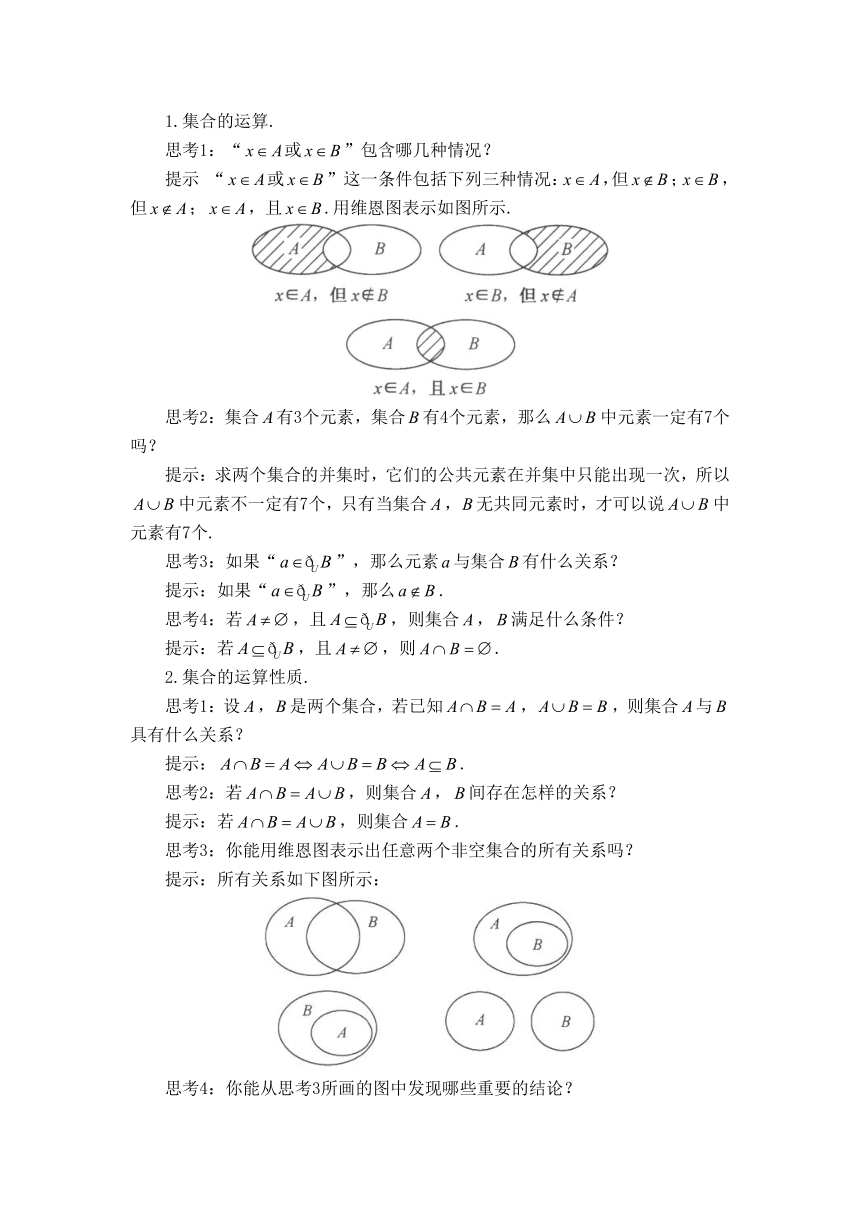
思考1:“或”包含哪几种情况?
提示 “或”这一条件包括下列三种情况:,但;,但;,且.用维恩图表示如图所示.
思考2:集合有3个元素,集合有4个元素,那么中元素一定有7个吗?
提示:求两个集合的并集时,它们的公共元素在并集中只能出现一次,所以中元素不一定有7个,只有当集合,无共同元素时,才可以说中元素有7个.
思考3:如果“”,那么元素与集合有什么关系?
提示:如果“”,那么.
思考4:若,且,则集合,满足什么条件?
提示:若,且,则.
2.集合的运算性质.
思考1:设,是两个集合,若已知,,则集合与具有什么关系?
提示:.
思考2:若,则集合,间存在怎样的关系?
提示:若,则集合.
思考3:你能用维恩图表示出任意两个非空集合的所有关系吗?
提示:所有关系如下图所示:
思考4:你能从思考3所画的图中发现哪些重要的结论?
提示:发现的结论如下:
由维恩图,我们观察到:
,,,,,;,,.
三、例题剖析
例1 已知,,全集,求,,.
想一想1:如何求两个集合的交集?
想一想2:如何求两个集合的并集?
想一想3:如何求给定集合的补集?
解:将或及在数轴上表示出来,如图所示:
则数轴上方所有“线”下面的实数组成了,
故.
数轴上方“双线”(即公共部分)下面的实数组成了,故.
数轴上除去或之外的数组成了的补集,故.
练习:教材第20页习题1-1A第9、10题.
归纳总结:
1.两个集合求交集,结果还是一个集合,是由集合与的公共元素组成的集合.当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集.
2.两个集合求并集,结果还是一个集合,是由集合与的所有元素组成的集合(重复元素只看成一个元素).
3.给定集合求补集,结果还是一个集合,是由全集中不属于的元素组成的集合,补集必须要有全集的限制.
例2 已知集合,集合.若,求实数的取值范围.
想一想1:集合能否是空集?
想一想2:是否说明两个集合没有共同的元素?
想一想3:空集与任一个集合的交集是什么?
解:由,得
①若,即时,,符合题意;
②若,即时,需或解得或,即.
综上可知,即实数的取值范围为.
练习:教材第21页习题1-1C第1~3题.
归纳总结:
利用集合的运算性质求参数的取值范围时,当两个集合出现交集为空集的情形,应首先考虑已知集合有没有可能为空集.确定不是空集后,在数轴上标出两个集合,利用不等式确定参数所需要满足的条件,从而解出参数的取值范围.
例3 设,,已知,求实数的值.
想一想1:集合,中的元素满足互异性吗?
想一想2:可得出什么结论?
解:,,则或.
或.
当时,,,符合题意;
当时,,,与集合中元素的互异性矛盾,故不合题意;
当时,,,与矛盾,故不合题意.
综上可得.
变式思考:
若将条件,改为,又该如何求解?
四、巩固提升
教材第21页习题1-1B第3~6题.
板书设计
1.1.3 集合的基本运算 一、阅读引导 集合的运算: (1) (2) (3) 二、知识深化 1.交集、并集、补集的运算 2.集合运算性质的应用 三、例题剖析 例1 例2 例3 四、巩固提升
教学研讨
由于本节课内容比较容易接受,也是历年高考的必考内容之一,所以在教学设计上应注重加强练习和拓展教材内容.设计中通过借助于数轴或维恩图写出集合运算的结果,这是突破本节教学难点的有效方法.
教学设计
一、阅读引导
1.阅读教材,问题导入.
阅读教材第14~19页内容,回答下列问题.
考察下列各个集合,你能说出集合与集合,之间的关系吗?
①,,;
②,,;
③,,.
提示:集合与集合,之间的关系是:
①;
②;
③设全集,则.
2.归纳总结,核心必记.
(1)一般地,给定两个集合,,由既属于又属于的所有元素(即和的公共元素)组成的集合,称为与的交集,记作,读作“交”,图示为:
(2)一般地,给定两个集合,,由这两个集合的所有元素组成的集合,称为与的并集,记作,读作“并”,图示为(1)或(2):
(3)如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,全集通常用表示.如果集合是全集的一个子集,则由中不属于的所有元素组成的集合,称为在中的补集,记作,读作“在中的补集”,图示为:
二、知识深化
1.集合的运算.
思考1:“或”包含哪几种情况?
提示 “或”这一条件包括下列三种情况:,但;,但;,且.用维恩图表示如图所示.
思考2:集合有3个元素,集合有4个元素,那么中元素一定有7个吗?
提示:求两个集合的并集时,它们的公共元素在并集中只能出现一次,所以中元素不一定有7个,只有当集合,无共同元素时,才可以说中元素有7个.
思考3:如果“”,那么元素与集合有什么关系?
提示:如果“”,那么.
思考4:若,且,则集合,满足什么条件?
提示:若,且,则.
2.集合的运算性质.
思考1:设,是两个集合,若已知,,则集合与具有什么关系?
提示:.
思考2:若,则集合,间存在怎样的关系?
提示:若,则集合.
思考3:你能用维恩图表示出任意两个非空集合的所有关系吗?
提示:所有关系如下图所示:
思考4:你能从思考3所画的图中发现哪些重要的结论?
提示:发现的结论如下:
由维恩图,我们观察到:
,,,,,;,,.
三、例题剖析
例1 已知,,全集,求,,.
想一想1:如何求两个集合的交集?
想一想2:如何求两个集合的并集?
想一想3:如何求给定集合的补集?
解:将或及在数轴上表示出来,如图所示:
则数轴上方所有“线”下面的实数组成了,
故.
数轴上方“双线”(即公共部分)下面的实数组成了,故.
数轴上除去或之外的数组成了的补集,故.
练习:教材第20页习题1-1A第9、10题.
归纳总结:
1.两个集合求交集,结果还是一个集合,是由集合与的公共元素组成的集合.当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集.
2.两个集合求并集,结果还是一个集合,是由集合与的所有元素组成的集合(重复元素只看成一个元素).
3.给定集合求补集,结果还是一个集合,是由全集中不属于的元素组成的集合,补集必须要有全集的限制.
例2 已知集合,集合.若,求实数的取值范围.
想一想1:集合能否是空集?
想一想2:是否说明两个集合没有共同的元素?
想一想3:空集与任一个集合的交集是什么?
解:由,得
①若,即时,,符合题意;
②若,即时,需或解得或,即.
综上可知,即实数的取值范围为.
练习:教材第21页习题1-1C第1~3题.
归纳总结:
利用集合的运算性质求参数的取值范围时,当两个集合出现交集为空集的情形,应首先考虑已知集合有没有可能为空集.确定不是空集后,在数轴上标出两个集合,利用不等式确定参数所需要满足的条件,从而解出参数的取值范围.
例3 设,,已知,求实数的值.
想一想1:集合,中的元素满足互异性吗?
想一想2:可得出什么结论?
解:,,则或.
或.
当时,,,符合题意;
当时,,,与集合中元素的互异性矛盾,故不合题意;
当时,,,与矛盾,故不合题意.
综上可得.
变式思考:
若将条件,改为,又该如何求解?
四、巩固提升
教材第21页习题1-1B第3~6题.
板书设计
1.1.3 集合的基本运算 一、阅读引导 集合的运算: (1) (2) (3) 二、知识深化 1.交集、并集、补集的运算 2.集合运算性质的应用 三、例题剖析 例1 例2 例3 四、巩固提升
教学研讨
由于本节课内容比较容易接受,也是历年高考的必考内容之一,所以在教学设计上应注重加强练习和拓展教材内容.设计中通过借助于数轴或维恩图写出集合运算的结果,这是突破本节教学难点的有效方法.
