人教A版(2019)高中数学选择性必修第三册 7.5《正态分布》名师课件(共24张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 7.5《正态分布》名师课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 13:32:15 | ||
图片预览








文档简介
(共24张PPT)
情境引入
已知服从参数为的二项分布,即,你能手工计算出的值吗
人教A版同步教材名师课件
正态分布
学习目标
学 习 目 标 核心素养
了解正态曲线的特点及参数的意义 直观想象
能根据对称性求正态分布的概率问题 逻辑推理
能利用正态分布解决一些实际问题 数学建模
学习目标
学习目标:
1.借助正态曲线理解正态分布的含义与性质.
2.求正态分布在某个区间的概率及灵活运用正态分布解决简单实际问题.
学科核心素养:
创设教学情境,通过采用引导发现、自主探究、讲练结合、问题引领等方法,让学生的思维活动在教师的引导和问题的引领下层层展开通过类比、数形结合等多种方式,加深学生对正态分布的认识,提高学生直观想象、逻辑推理等核心素养,培养学生对数学概念的理解能力和应用能力.
探究新知
因为,
所以,如果要手工计算),是一个“几乎不可能”完成的任务,
即使是一般的计算器也难以胜任类似的计算.事实上,利用计算机软件可知
因此
探究新知
由此可以看出,如果随机变量,那么较大时,直接计算
将是十分困难的.有没有其他办法能得到上式的近似值呢?这正是18世纪30年代数学家棣莫弗所研究过的问题.在讨论这个问题的过程中,棣莫弗发现了本小节我们要学习的正态曲线
探究新知
1.正态曲线的定义:
函数,其中的实数是参数,分别表示总体的平均数与标准差,称的图象称为正态曲线
一般地,如果随机变量落在区间内的概率,总是等于对应的正态曲线与轴在区间内围成的面积,则称服从参数为与的正态分布,记作
2.正态分布的定义:
探究新知
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
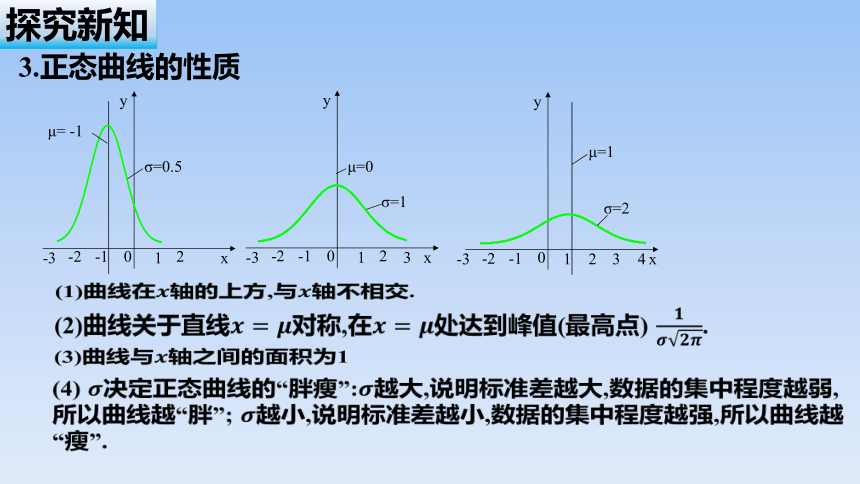
(1)曲线在轴的上方,与轴不相交.
(2)曲线关于直线对称,在处达到峰值(最高点) .
3.正态曲线的性质
(3)曲线与轴之间的面积为1
(4) 决定正态曲线的“胖瘦”:越大,说明标准差越大,数据的集中程度越弱,所以曲线越“胖”; 越小,说明标准差越小,数据的集中程度越强,所以曲线越“瘦”.
典例讲解
例1、如图所示是一个正态曲线,试根据该图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的期望和方差.
从给出的正态曲线可知,该正态曲线关于
直线对称,最大值是,所以.
由,得.
于是概率密度函数的解析式是
,
总体随机变量的期望是,方差是.
解析
方法归纳
利用正态曲线的性质可以求参数,具体方法如下:
(1)正态曲线是单峰的,它关于直线对称,由此性质结合图象求.
(2)正态曲线在处达到峰值,由此性质结合图象可求.
变式训练
1.设两个正态分布N(,)()和N(,)()的密度函数图象如图所示,则有( )
A. B.
C. D.
根据正态分布的性质:对称轴方程表示正态曲线的形状.由题图可得
解析
A
典例讲解
∵随机变量服从正态分布,
∴,对称轴是.
∵,
∴,
∴,
∴.
例2、已知随机变量ξ服从正态分布,且,则( )
A.0.6 B.0.4 C.0.3 D.0.2
解析
C
方法归纳
1.对称法:由于正态曲线是关于直线对称的,且概率的和为1,故关于直线对称的区间上概率相等.如:
(1);
(2).
2. “ ”法:利用落在区间
内的概率分别是求解.
利用正态分布求概率的两个方法
变式训练
2.设随机变量,若.
(1)求的值;
(2)求.
(1)由 可知,密度函数关于直线对称(如图所示),
又 ,故有,
所以.
(2) .
解析
典例讲解
∵
∴,
∴.
∴ (人),即及格人数约为45人.
∵ ,
∴
例3、设在一次数学考试中,某班学生的分数,且知试卷满分150分,这个班的学生共54人,求这个班在这次数学考试中及格(即90分以上)的人数和130分以上的人数.
解析
典例讲解
,
∴,即P.
∴ (人),即130分以上的人数约为9人.
例3、设在一次数学考试中,某班学生的分数,且知试卷满分150分,这个班的学生共54人,求这个班在这次数学考试中及格(即90分以上)的人数和130分以上的人数.
解析
方法归纳
1.本题利用转化的思想方法,把普通的区间转化为3σ区间,由特殊区间的概率值求出.
2.解答正态分布的实际应用题,其关键是如何转化,同时应熟练掌握正态分布在三个区间内的概率.在此过程中用到归纳思想和数形结合思想.
变式训练
解析
3.某人从某城市的南郊乘公交车前往北区火车站,由于交通拥挤,所需时间(单位:分)近似服从正态分布,求他在分内赶到火车站的概率.
∵ ,∴.
∴
.
即他在分内赶到火车站的概率是.
素养提炼
1.若是两个随机变量,且,则.如果一个随机变量服从两点分布或二项分布,可直接利用公式计算均值
2.随机变量的方差和标准差都反映了随机变量取值的稳定与波动、集中与离散的程度,以及随机变量取值偏离于均值的平均程度.方差或标准差越小,则随机变量偏离均值的平均程度越小;方差越大,表明偏离均值的平均程度越大,说明的取值越分散
3.求离散型随机变量的均值、方差的步骤.
(1)理解的意义,写出的所有可能的取值;
(2)求取每一个值的概率;
(3)写出随机变量的分布列;
(4)由均值、方差的定义求
特别地,若随机变量服从两点分布或二项分布,可根据对应公式直接计算和
1.如图是当取三个不同值,,的三种正态曲线的图象,那么的大小关系是( )
A.
B.
C.
D.
当时,正态曲线.在时,取最大值,故.由正态曲线的性质,当一定时,曲线的形状由确定.越小,曲线越“瘦高”;越大,曲线越“矮胖”,于是有.
解析
当堂练习
D
2.已知随机变量服从正态分布,且,则________.
当堂练习
由,可知其正态曲线如图所示,
对称轴为,则.
解析
当堂练习
3.随机变量服从正态分布,如果,求.
解析
如图所示,
因为,
所以,
所以,
所以.
归纳小结
正态分布
二项分布与正态曲线
标准正态分布
正态分布
作 业
课本P87 习题7.5: 2,3
情境引入
已知服从参数为的二项分布,即,你能手工计算出的值吗
人教A版同步教材名师课件
正态分布
学习目标
学 习 目 标 核心素养
了解正态曲线的特点及参数的意义 直观想象
能根据对称性求正态分布的概率问题 逻辑推理
能利用正态分布解决一些实际问题 数学建模
学习目标
学习目标:
1.借助正态曲线理解正态分布的含义与性质.
2.求正态分布在某个区间的概率及灵活运用正态分布解决简单实际问题.
学科核心素养:
创设教学情境,通过采用引导发现、自主探究、讲练结合、问题引领等方法,让学生的思维活动在教师的引导和问题的引领下层层展开通过类比、数形结合等多种方式,加深学生对正态分布的认识,提高学生直观想象、逻辑推理等核心素养,培养学生对数学概念的理解能力和应用能力.
探究新知
因为,
所以,如果要手工计算),是一个“几乎不可能”完成的任务,
即使是一般的计算器也难以胜任类似的计算.事实上,利用计算机软件可知
因此
探究新知
由此可以看出,如果随机变量,那么较大时,直接计算
将是十分困难的.有没有其他办法能得到上式的近似值呢?这正是18世纪30年代数学家棣莫弗所研究过的问题.在讨论这个问题的过程中,棣莫弗发现了本小节我们要学习的正态曲线
探究新知
1.正态曲线的定义:
函数,其中的实数是参数,分别表示总体的平均数与标准差,称的图象称为正态曲线
一般地,如果随机变量落在区间内的概率,总是等于对应的正态曲线与轴在区间内围成的面积,则称服从参数为与的正态分布,记作
2.正态分布的定义:
探究新知
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
(1)曲线在轴的上方,与轴不相交.
(2)曲线关于直线对称,在处达到峰值(最高点) .
3.正态曲线的性质
(3)曲线与轴之间的面积为1
(4) 决定正态曲线的“胖瘦”:越大,说明标准差越大,数据的集中程度越弱,所以曲线越“胖”; 越小,说明标准差越小,数据的集中程度越强,所以曲线越“瘦”.
典例讲解
例1、如图所示是一个正态曲线,试根据该图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的期望和方差.
从给出的正态曲线可知,该正态曲线关于
直线对称,最大值是,所以.
由,得.
于是概率密度函数的解析式是
,
总体随机变量的期望是,方差是.
解析
方法归纳
利用正态曲线的性质可以求参数,具体方法如下:
(1)正态曲线是单峰的,它关于直线对称,由此性质结合图象求.
(2)正态曲线在处达到峰值,由此性质结合图象可求.
变式训练
1.设两个正态分布N(,)()和N(,)()的密度函数图象如图所示,则有( )
A. B.
C. D.
根据正态分布的性质:对称轴方程表示正态曲线的形状.由题图可得
解析
A
典例讲解
∵随机变量服从正态分布,
∴,对称轴是.
∵,
∴,
∴,
∴.
例2、已知随机变量ξ服从正态分布,且,则( )
A.0.6 B.0.4 C.0.3 D.0.2
解析
C
方法归纳
1.对称法:由于正态曲线是关于直线对称的,且概率的和为1,故关于直线对称的区间上概率相等.如:
(1);
(2).
2. “ ”法:利用落在区间
内的概率分别是求解.
利用正态分布求概率的两个方法
变式训练
2.设随机变量,若.
(1)求的值;
(2)求.
(1)由 可知,密度函数关于直线对称(如图所示),
又 ,故有,
所以.
(2) .
解析
典例讲解
∵
∴,
∴.
∴ (人),即及格人数约为45人.
∵ ,
∴
例3、设在一次数学考试中,某班学生的分数,且知试卷满分150分,这个班的学生共54人,求这个班在这次数学考试中及格(即90分以上)的人数和130分以上的人数.
解析
典例讲解
,
∴,即P.
∴ (人),即130分以上的人数约为9人.
例3、设在一次数学考试中,某班学生的分数,且知试卷满分150分,这个班的学生共54人,求这个班在这次数学考试中及格(即90分以上)的人数和130分以上的人数.
解析
方法归纳
1.本题利用转化的思想方法,把普通的区间转化为3σ区间,由特殊区间的概率值求出.
2.解答正态分布的实际应用题,其关键是如何转化,同时应熟练掌握正态分布在三个区间内的概率.在此过程中用到归纳思想和数形结合思想.
变式训练
解析
3.某人从某城市的南郊乘公交车前往北区火车站,由于交通拥挤,所需时间(单位:分)近似服从正态分布,求他在分内赶到火车站的概率.
∵ ,∴.
∴
.
即他在分内赶到火车站的概率是.
素养提炼
1.若是两个随机变量,且,则.如果一个随机变量服从两点分布或二项分布,可直接利用公式计算均值
2.随机变量的方差和标准差都反映了随机变量取值的稳定与波动、集中与离散的程度,以及随机变量取值偏离于均值的平均程度.方差或标准差越小,则随机变量偏离均值的平均程度越小;方差越大,表明偏离均值的平均程度越大,说明的取值越分散
3.求离散型随机变量的均值、方差的步骤.
(1)理解的意义,写出的所有可能的取值;
(2)求取每一个值的概率;
(3)写出随机变量的分布列;
(4)由均值、方差的定义求
特别地,若随机变量服从两点分布或二项分布,可根据对应公式直接计算和
1.如图是当取三个不同值,,的三种正态曲线的图象,那么的大小关系是( )
A.
B.
C.
D.
当时,正态曲线.在时,取最大值,故.由正态曲线的性质,当一定时,曲线的形状由确定.越小,曲线越“瘦高”;越大,曲线越“矮胖”,于是有.
解析
当堂练习
D
2.已知随机变量服从正态分布,且,则________.
当堂练习
由,可知其正态曲线如图所示,
对称轴为,则.
解析
当堂练习
3.随机变量服从正态分布,如果,求.
解析
如图所示,
因为,
所以,
所以,
所以.
归纳小结
正态分布
二项分布与正态曲线
标准正态分布
正态分布
作 业
课本P87 习题7.5: 2,3
