人教A版(2019)高中数学选择性必修第三册 7.5正态分布 课件(共27张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 7.5正态分布 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 566.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 13:33:01 | ||
图片预览








文档简介
(共27张PPT)
随机变量及其分布
第七章
7.5 正态分布
课程内容标准 学科素养凝练
1.通过误差模型,了解服从正态分布的随机变量. 2.通过具体实例,借助频率分布直方图的几何直观,了解正态分布的特征. 3.了解正态分布的均值、方差及其含义. 1.在理解正态分布概念过程中,提升数学抽象的学科素养.
2.利用求解正态分布问题过程中,增强逻辑推理、数学运算和数学建模的核心素养.
课前 预习案
(1)正态曲线:对于给定函数f(x)=__________,x∈R,其中μ∈R,σ>0为参数.我们称f(x)为_______________,它的图象为正态密度曲线,简称___________.
(2)正态分布与标准正态分布:若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布,记作X~___________.特别地,当_______,_______时,称随机变量X服从标准正态分布.
一、正态分布
正态密度函数
正态曲线
N(μ,σ2)
μ=0
σ=1
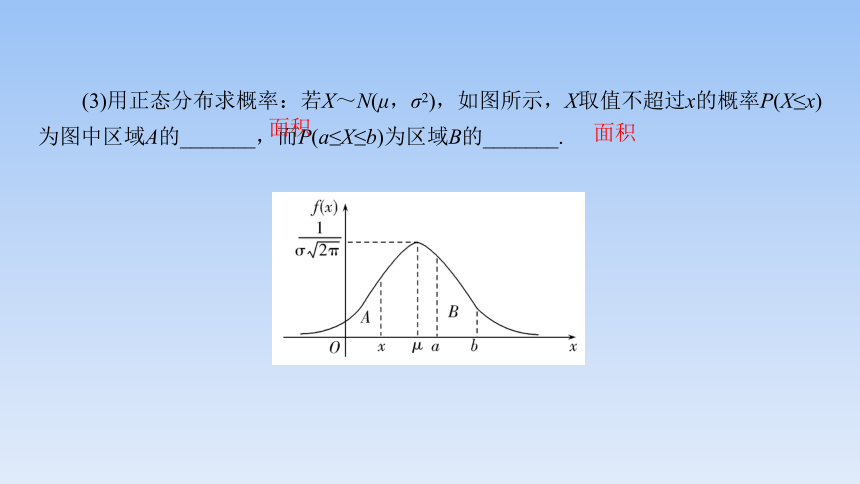
(3)用正态分布求概率:若X~N(μ,σ2),如图所示,X取值不超过x的概率P(X≤x)为图中区域A的_______,而P(a≤X≤b)为区域B的_______.
面积
面积
(4)正态曲线的特点
①正态曲线在x轴的_______;
②正态曲线与x轴之间的区域的面积为____;
③曲线是_______的,它关于直线_______对称;
④曲线在x=μ处达到峰值__________;
⑤当|x|无限增大时,曲线无限接近x轴.
上方
1
单峰
x=μ
⑥μ决定正态曲线的位置:当参数取固定值时,正态曲线的位置由μ确定,如图(1)所示;
⑦σ决定正态曲线的“胖瘦”:当σ较小时,峰值高,曲线“_______”,表示随机变量的分布比较_______;当σ较大时,峰值低,曲线“_______”,表示随机变量X的分布比较_______,如图(2)所示.
(5)正态分布的均值和方差:若X~N(μ,σ2),则E(X)=____,D(X)=_____.
瘦高
集中
矮胖
分散
μ
σ2
如果X~N(μ,σ2),那么P(X≤μ)=P(X≥μ)=______,
P(μ-σ≤X≤μ+σ)≈__________,
P(μ-2σ≤X≤μ+2σ)≈__________,
P(μ-3σ≤X≤μ+3σ)≈__________.
尽管正态变量的取值范围是(-∞,+∞),但在一次试验中,X的取值几乎总是落在区间___________________内,而在此区间以外取值的概率大约只有0.002 7,通常认为这种情况几乎_____________.在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值.
二、“3σ原则”
0.5
0.682 7
0.954 5
0.997 3
[μ-3σ,μ+3σ]
不可能发生
1.判断下列说法是否正确,正确的在它后面的括号里打“√”,错误的打“×”.
(1)正态变量函数表述式中参数μ,σ的意义分别是样本的均值与方差.( )
(2)正态曲线是单峰的,其与x轴围成的面积是随参数μ,σ的变化而变化的.
( )
(3)正态曲线可以关于y轴对称. ( )
(4)当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,σ越大,曲线越“矮胖”. ( )
答案 (1)× (2)× (3)× (4)√
3.(多选题)把一条正态曲线a沿着横轴方向向右移动2个单位,得到一条新的曲线b,下列说法中正确的是 ( )
A.曲线b仍然是正态曲线
B.曲线a和曲线b的最高点的纵坐标相等
C.以曲线b为正态分布的总体的方差比以曲线a为正态分布的总体的方差大2
D.以曲线b为正态分布的总体的均值比以曲线a为正态分布的总体的均值大2
答案 ABD
解析 正态曲线向右平移2个单位,σ不发生变化,故C错误,其他正确.
课堂 探究案
探究一 正态曲线的图象及其应用
答案 A
解析 根据正态曲线的特征:对称轴方程x=μ,σ表示正态曲线的形状.由图可得,选A.
(2)如图所示是一个正态曲线,试根据该图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的均值和方差.
答案 D
解析 因为正态曲线关于x=μ对称,且μ越大图象越靠近右边,所以可得μ1<μ2=μ3,又因为σ的值反映的是这组数据的集中情况,其σ值越小图象越瘦长,σ值越大图象越矮胖,所以可得σ1=σ2<σ3.
(1)已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)= ( )
A.0.6 B.0.4
C.0.3 D.0.2
答案 C
解析 ∵随机变量X服从正态分布N(2,σ2),∴μ=2,对称轴是x=2.
∵P(ξ<4)=0.8,∴P(ξ≥4)=P(ξ<0)=0.2,∴P(0<ξ<4)=0.6.∴P(0<ξ<2)=0.3.
探究二 服从正态分布变量的概率问题
(2)在某项测量中,测量结果服从正态分布N(1,4),求正态总体X在(-1,1)内取值的概率.
[变式] 本例(2)中已知条件不变,试求P(X≥5).
[方法总结] 利用正态分布求概率的两个方法
(1)对称法:由于正态曲线是关于直线x=μ对称的,且概率的和为1,故关于直线x=μ对称的区间上概率相等.如:
①P(X②P(X<μ-a)=P(X>μ+a).
(2)“3σ”法:利用X落在区间(μ-σ,μ+σ],(μ-2σ,μ+2σ],(μ-3σ,μ+3σ]内的概率分别是0.682 7, 0.954 5,0.997 3求解.
[训练2] 已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.682 7,则P(X>4)= ( )
A.0.158 5 B.0.158 6
C.0.158 7 D.0.341 3
答案 C
在某次数学考试中,考生的成绩X服从一个正态分布,即X~N(90,100).
(1)试求考试成绩X位于区间[70,110]内的概率是多少?
(2)若这次考试共有2 000名考生,试估计考试成绩在[80,100]之间的考生大约有多少人?
探究三 正态分布的实际应用
[方法总结]
解答正态分布的实际应用题,其关键是如何转化,同时应熟练掌握正态分布在[μ-σ,μ+σ],[μ-2σ,μ+2σ],[μ-3σ,μ+3σ]三个区间内的概率.在此过程中用到归纳思想和数形结合思想.
[训练3] 某城市从南郊某地乘公共汽车前往北区火车站有两条路线可走,第一条路线穿过市区,路线较短,但交通拥挤,所需时间(单位为分)服从正态分布N(50,102);第二条路线沿环城公路走,路程较长,但交通阻塞少,所需时间服从正态分布N(60,42).
(1)若只有70分钟可用,问应走哪条路线?
(2)若只有65分钟可用,又应走哪条路线?
解 由已知X~N(50,102),Y~N(60,42).
由正态分布的2σ区间性质P(μ-2σ≤ξ≤μ+2σ)=0.954 5.
然后解决问题的关键是:根据上述性质得到如下结果:
对X:μ=50;σ=10;2σ区间为(30,70),
对Y:μ=60;σ=4,2σ区间为(52,68),
要尽量保证用时在X (30,70),Y (52,68)才能保证有95%以上的概率准时到达.
(1)时间只有70分钟可用,应该走第二条路线.
(2)时间只有65分钟可用,两种方案都能保证有95%以上的概率准时到达,但是走市区平均用时比路线二少了10分钟,应该走第一条路线.
随机变量及其分布
第七章
7.5 正态分布
课程内容标准 学科素养凝练
1.通过误差模型,了解服从正态分布的随机变量. 2.通过具体实例,借助频率分布直方图的几何直观,了解正态分布的特征. 3.了解正态分布的均值、方差及其含义. 1.在理解正态分布概念过程中,提升数学抽象的学科素养.
2.利用求解正态分布问题过程中,增强逻辑推理、数学运算和数学建模的核心素养.
课前 预习案
(1)正态曲线:对于给定函数f(x)=__________,x∈R,其中μ∈R,σ>0为参数.我们称f(x)为_______________,它的图象为正态密度曲线,简称___________.
(2)正态分布与标准正态分布:若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布,记作X~___________.特别地,当_______,_______时,称随机变量X服从标准正态分布.
一、正态分布
正态密度函数
正态曲线
N(μ,σ2)
μ=0
σ=1
(3)用正态分布求概率:若X~N(μ,σ2),如图所示,X取值不超过x的概率P(X≤x)为图中区域A的_______,而P(a≤X≤b)为区域B的_______.
面积
面积
(4)正态曲线的特点
①正态曲线在x轴的_______;
②正态曲线与x轴之间的区域的面积为____;
③曲线是_______的,它关于直线_______对称;
④曲线在x=μ处达到峰值__________;
⑤当|x|无限增大时,曲线无限接近x轴.
上方
1
单峰
x=μ
⑥μ决定正态曲线的位置:当参数取固定值时,正态曲线的位置由μ确定,如图(1)所示;
⑦σ决定正态曲线的“胖瘦”:当σ较小时,峰值高,曲线“_______”,表示随机变量的分布比较_______;当σ较大时,峰值低,曲线“_______”,表示随机变量X的分布比较_______,如图(2)所示.
(5)正态分布的均值和方差:若X~N(μ,σ2),则E(X)=____,D(X)=_____.
瘦高
集中
矮胖
分散
μ
σ2
如果X~N(μ,σ2),那么P(X≤μ)=P(X≥μ)=______,
P(μ-σ≤X≤μ+σ)≈__________,
P(μ-2σ≤X≤μ+2σ)≈__________,
P(μ-3σ≤X≤μ+3σ)≈__________.
尽管正态变量的取值范围是(-∞,+∞),但在一次试验中,X的取值几乎总是落在区间___________________内,而在此区间以外取值的概率大约只有0.002 7,通常认为这种情况几乎_____________.在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值.
二、“3σ原则”
0.5
0.682 7
0.954 5
0.997 3
[μ-3σ,μ+3σ]
不可能发生
1.判断下列说法是否正确,正确的在它后面的括号里打“√”,错误的打“×”.
(1)正态变量函数表述式中参数μ,σ的意义分别是样本的均值与方差.( )
(2)正态曲线是单峰的,其与x轴围成的面积是随参数μ,σ的变化而变化的.
( )
(3)正态曲线可以关于y轴对称. ( )
(4)当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,σ越大,曲线越“矮胖”. ( )
答案 (1)× (2)× (3)× (4)√
3.(多选题)把一条正态曲线a沿着横轴方向向右移动2个单位,得到一条新的曲线b,下列说法中正确的是 ( )
A.曲线b仍然是正态曲线
B.曲线a和曲线b的最高点的纵坐标相等
C.以曲线b为正态分布的总体的方差比以曲线a为正态分布的总体的方差大2
D.以曲线b为正态分布的总体的均值比以曲线a为正态分布的总体的均值大2
答案 ABD
解析 正态曲线向右平移2个单位,σ不发生变化,故C错误,其他正确.
课堂 探究案
探究一 正态曲线的图象及其应用
答案 A
解析 根据正态曲线的特征:对称轴方程x=μ,σ表示正态曲线的形状.由图可得,选A.
(2)如图所示是一个正态曲线,试根据该图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的均值和方差.
答案 D
解析 因为正态曲线关于x=μ对称,且μ越大图象越靠近右边,所以可得μ1<μ2=μ3,又因为σ的值反映的是这组数据的集中情况,其σ值越小图象越瘦长,σ值越大图象越矮胖,所以可得σ1=σ2<σ3.
(1)已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)= ( )
A.0.6 B.0.4
C.0.3 D.0.2
答案 C
解析 ∵随机变量X服从正态分布N(2,σ2),∴μ=2,对称轴是x=2.
∵P(ξ<4)=0.8,∴P(ξ≥4)=P(ξ<0)=0.2,∴P(0<ξ<4)=0.6.∴P(0<ξ<2)=0.3.
探究二 服从正态分布变量的概率问题
(2)在某项测量中,测量结果服从正态分布N(1,4),求正态总体X在(-1,1)内取值的概率.
[变式] 本例(2)中已知条件不变,试求P(X≥5).
[方法总结] 利用正态分布求概率的两个方法
(1)对称法:由于正态曲线是关于直线x=μ对称的,且概率的和为1,故关于直线x=μ对称的区间上概率相等.如:
①P(X
(2)“3σ”法:利用X落在区间(μ-σ,μ+σ],(μ-2σ,μ+2σ],(μ-3σ,μ+3σ]内的概率分别是0.682 7, 0.954 5,0.997 3求解.
[训练2] 已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.682 7,则P(X>4)= ( )
A.0.158 5 B.0.158 6
C.0.158 7 D.0.341 3
答案 C
在某次数学考试中,考生的成绩X服从一个正态分布,即X~N(90,100).
(1)试求考试成绩X位于区间[70,110]内的概率是多少?
(2)若这次考试共有2 000名考生,试估计考试成绩在[80,100]之间的考生大约有多少人?
探究三 正态分布的实际应用
[方法总结]
解答正态分布的实际应用题,其关键是如何转化,同时应熟练掌握正态分布在[μ-σ,μ+σ],[μ-2σ,μ+2σ],[μ-3σ,μ+3σ]三个区间内的概率.在此过程中用到归纳思想和数形结合思想.
[训练3] 某城市从南郊某地乘公共汽车前往北区火车站有两条路线可走,第一条路线穿过市区,路线较短,但交通拥挤,所需时间(单位为分)服从正态分布N(50,102);第二条路线沿环城公路走,路程较长,但交通阻塞少,所需时间服从正态分布N(60,42).
(1)若只有70分钟可用,问应走哪条路线?
(2)若只有65分钟可用,又应走哪条路线?
解 由已知X~N(50,102),Y~N(60,42).
由正态分布的2σ区间性质P(μ-2σ≤ξ≤μ+2σ)=0.954 5.
然后解决问题的关键是:根据上述性质得到如下结果:
对X:μ=50;σ=10;2σ区间为(30,70),
对Y:μ=60;σ=4,2σ区间为(52,68),
要尽量保证用时在X (30,70),Y (52,68)才能保证有95%以上的概率准时到达.
(1)时间只有70分钟可用,应该走第二条路线.
(2)时间只有65分钟可用,两种方案都能保证有95%以上的概率准时到达,但是走市区平均用时比路线二少了10分钟,应该走第一条路线.
