人教A版(2019)高中数学选择性必修第三册 《随机变量及其分布》章末复习课件(共26张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 《随机变量及其分布》章末复习课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 720.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
《随机变量及其分布》章末复习
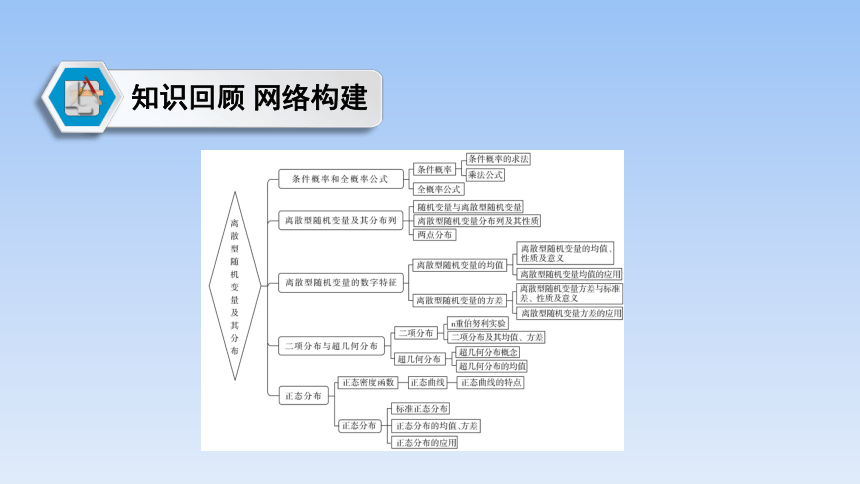
知识回顾 网络构建
一、条件概率
综合题型 归纳总结
[训练1] 在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
二、离散型随机变量的分布列
离散型随机变量分布列表格形式的结构特征
分布列的结构为两行,第一行为随机变量的所有可能取得的值;第二行为对应于随机变量取值的事件发生的概率.看每一列,实际上是:上为“事件”,下为事件发生的概率.
三、离散型随机变量的期望与方差
求离散型随机变量ξ的期望与方差的步骤
答案 A
解析 E(X1)=E(X2)=1.1,D(X1)=1.12×0.2+0.12×0.5+0.92×0.3=0.49,D(X2)=1.12×0.3+0.12×0.3+0.92×0.4=0.69,∴D(X1)[训练4] 某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4.现从这10人中随机选出2人作为该组代表参加座谈会.
(1)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率.
(2)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列和数学期望.
四、二项分布
1.判断一个随机变量是否服从二项分布的关键
(1)对立性,即一次试验中,事件发生与否二者必居其一.
(2)重复性,即试验独立重复地进行了n次.
(3)随机变量是事件发生的次数.
2.二项分布实际应用问题的解题思路
(1)根据题意设出随机变量.
(2)分析出随机变量服从二项分布.
(3)找到参数n(试验的次数)和p(事件发生的概率).
(4)写出二项分布的分布列.
[训练6] 一次同时投掷两枚相同的正方体骰子(骰子质地均匀,且各面分别刻有1,2,2,3,3,3六个数字).
(1)设随机变量η表示一次掷得的点数和,求η的分布列.
(2)若连续投掷10次,设随机变量ξ表示一次掷得的点数和大于5的次数,求E(ξ),D(ξ).
五、超几何分布
对超几何分布的三点说明
(1)超几何分布的模型是不放回抽样.
(2)超几何分布中的参数是M,N,n.
(3)超几何分布可解决产品中的正品和次品、盒中的白球和黑球、同学中的男和女等问题,往往由差异明显的两部分组成.
[训练8] 一个袋中装有3个白球和2个黑球,它们大小相同,采用无放回地方式从袋中任取3个球,取到黑球的数目用X表示,求随机变量X的分布列.
六、正态分布
正态分布的概率求法
(1)注意“3σ原则”的适用.记住正态总体在三个区间内取值的概率.
(2)注意数形结合.由于正态分布密度曲线具有完美的对称性,体现了数形结合的重要思想,因此运用对称性结合图象解决某一区间内的概率问题成为热点问题.
[训练10] 某学校高三2 500名学生第二次模拟考试总成绩服从正态分布N(500,502),请您判断考生成绩X在550~600分的人数.
《随机变量及其分布》章末复习
知识回顾 网络构建
一、条件概率
综合题型 归纳总结
[训练1] 在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
二、离散型随机变量的分布列
离散型随机变量分布列表格形式的结构特征
分布列的结构为两行,第一行为随机变量的所有可能取得的值;第二行为对应于随机变量取值的事件发生的概率.看每一列,实际上是:上为“事件”,下为事件发生的概率.
三、离散型随机变量的期望与方差
求离散型随机变量ξ的期望与方差的步骤
答案 A
解析 E(X1)=E(X2)=1.1,D(X1)=1.12×0.2+0.12×0.5+0.92×0.3=0.49,D(X2)=1.12×0.3+0.12×0.3+0.92×0.4=0.69,∴D(X1)
(1)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率.
(2)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列和数学期望.
四、二项分布
1.判断一个随机变量是否服从二项分布的关键
(1)对立性,即一次试验中,事件发生与否二者必居其一.
(2)重复性,即试验独立重复地进行了n次.
(3)随机变量是事件发生的次数.
2.二项分布实际应用问题的解题思路
(1)根据题意设出随机变量.
(2)分析出随机变量服从二项分布.
(3)找到参数n(试验的次数)和p(事件发生的概率).
(4)写出二项分布的分布列.
[训练6] 一次同时投掷两枚相同的正方体骰子(骰子质地均匀,且各面分别刻有1,2,2,3,3,3六个数字).
(1)设随机变量η表示一次掷得的点数和,求η的分布列.
(2)若连续投掷10次,设随机变量ξ表示一次掷得的点数和大于5的次数,求E(ξ),D(ξ).
五、超几何分布
对超几何分布的三点说明
(1)超几何分布的模型是不放回抽样.
(2)超几何分布中的参数是M,N,n.
(3)超几何分布可解决产品中的正品和次品、盒中的白球和黑球、同学中的男和女等问题,往往由差异明显的两部分组成.
[训练8] 一个袋中装有3个白球和2个黑球,它们大小相同,采用无放回地方式从袋中任取3个球,取到黑球的数目用X表示,求随机变量X的分布列.
六、正态分布
正态分布的概率求法
(1)注意“3σ原则”的适用.记住正态总体在三个区间内取值的概率.
(2)注意数形结合.由于正态分布密度曲线具有完美的对称性,体现了数形结合的重要思想,因此运用对称性结合图象解决某一区间内的概率问题成为热点问题.
[训练10] 某学校高三2 500名学生第二次模拟考试总成绩服从正态分布N(500,502),请您判断考生成绩X在550~600分的人数.
